Теория: AB-тесты

В этом уроке мы обсудим AB-тестирование.

Как и ранее в курсе, возьмем два интерфейса — A и B. Попробуем определить, какой из них больше нравится пользователям. Для этого проведем эксперимент — покажем оба интерфейса двум независимым группам клиентов, а затем соберем данные об изменениях в их поведении.

Наша задача — выбрать самый лучший вариант и обосновать этот выбор. Чтобы это сделать нужно оценить надежность данных, собранных для обоих интерфейсов.

Нулевой гипотезой в нашем случае будет отсутствие зависимости между данными по кликам, а альтернативной - что между интерфейсами A и B есть разница.

Расчет статистических параметров

Представим, что по итогам тестирования мы получились следующую таблицу для версии A. Поле user_id - id пользователя сайта, а clicks - число кликов, которое он совершил на странице до ключевого действия, например, добавления товара в корзину.

И аналогичную таблицу для версии В:

Агрегируем данные:

И также для второй таблицы

Добавим еще один столбец с вероятностью каждого значения. Вероятность посчитаем как отношение количества кликов в ряду к общему числу кликов.

Теперь рассчитаем математическое ожидание как сумму произведений значений на их вероятности.

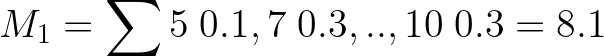
Также рассчитаем дисперсию выборки как

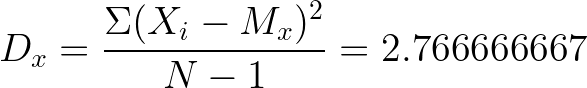
где X(i) значения в оригинальной (не агрегированной) таблице, M(x) мат.ожидание, а N размер оригинальной выборки, равный 10

Тогда, стандартное отклонение σ, корень из дисперсии, будет равно 1.663329993

Если вы работаете в Google таблицах, то стандартное отклонение можно получить с помощью функции STDEV(<диапазон выборки>)

Сделаем аналогичные расчеты для второго теста и перейдем к расчету критерия Стьюдента. Получим `

• M₂ = 11.3,
• D₂ = 2.233333333,
• σ₂ = 1.494434118

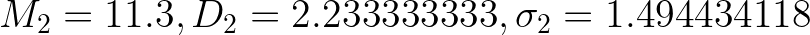
Критерий Стьюдента

Первый шаг — проверка распределения данных для определения их нормальности. В этом помогает t-распределение Стьюдента — это способ описания данных, которые при построении графика дает колоколообразную кривую (наибольшее число наблюдений находится вблизи среднего значения, наименьшее — в хвостах). Это разновидность нормального распределения, используемая при небольших объемах выборки, когда дисперсия данных неизвестна.

Критерий Стьюдента (t-коэффициент или t-критерий) — это количество стандартных отклонений от среднего значения в t-распределении. Обычно критерий Стьюдента можно найти в t-таблице или с помощью онлайн-калькулятора.

В статистике критерий Стьюдента помогает определить два параметра:

• Верхнюю и нижнюю границу доверительного интервала, когда данные распределены приблизительно нормально
• P-значение тестовой статистики для t-тестов и регрессионных тестов

Критерий Стьюдента позволяет определить, насколько случайны изменения в выборках и насколько они связаны друг с другом. Для примера представим, что при использовании интерфейса B появляются изменения в среднем чеке. Если вероятность ошибки невелика, то данные оказываются статистически значимыми — значит интерфейс B работает лучше.

Формула t-критерия Стьюдента для независимых выборок выглядит так:

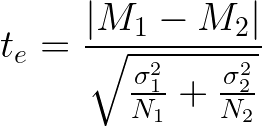
Рассмотрим ее подробнее:

• M₁ — среднее арифметическое первой выборки
• M₁ — среднее арифметическое первой выборки
• M₂ — среднее арифметическое второй выборки
• σ₁ — стандартное отклонение первой выборки
• σ₂ — стандартное отклонение второй выборки
• N₁ — объем первой выборки
• N₂ — объем второй выборки

Подставим полученные ранее данные, и рассчитаем критерий:

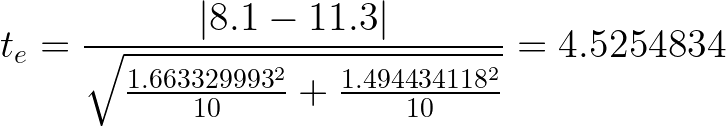
P-значение

Далее мы рассмотрим P-значение. Это уровень значимости, который показывает, с какой вероятностью данные подтверждают нулевую гипотезу.

Уровень значимости задается на начальном этапе и определяет максимальную вероятность совершения ошибки. Критические значения также определяются на основе этого уровня значимости и степени свободы. Если t-статистика меньше критического значения, то гипотеза о случайном характере изменений подтверждается — интерфейс B считается предпочтительным. В противном случае, мы выбираем интерфейс A.

Уровень значимости обычно составляет 5% или 1%, в очень редких случаях это 0,1%. Этот уровень доверия определяет, какие значения t будут считаться статистически значимыми. Чем ниже уровень значимости P, тем более строго анализируются данные и тем меньший разброс данных считается значимым.

Анализ исключает 5% значений на краях — они не учитываются при использовании выбранного уровня значимости. Вместо этого, анализ фокусируется на 95% наиболее часто встречающихся значений в выборке. Это позволяет оценить статистическую значимость изменений, исключить случайные факторы и сделать точный вывод о том, какой из интерфейсов предпочтительнее.

Обычно для определения значимости полученное значение критерия Стьюдента сравнивается с табличным.

Наш критерий равен 4.5254834, что больше табличного значения 3.922 для количества степеней свободы (N1 + N2) - 2. Получается, что уровень значимости меньше 0.001. При уровне меньше 0.05 мы делаем вывод о наличии различий между тестами и подтверждаем альтернативную гипотезу — "интерфейс B отличается от интерфейса A".

Практика

Посчитаем дисперсию и мат.ожидание для каждого из интерфейсов

SELECT
    version,
    SUM(category_count * probability) AS mo1,
    SUM(POWER(category_count,2) * probability) - POWER(SUM(category_count * probability), 2) as d1
FROM clickstream_ab
WHERE version = 1
GROUP BY 1
ORDER BY 1;

Ссылка на пример с вычислениями

Повторим расчеты для второго интерфейса

SELECT
    version,
    SUM(category_count * probability) AS mo2,
    SUM(POWER(category_count,2) * probability) - POWER(SUM(category_count * probability), 2) as d2
FROM clickstream_ab
WHERE version = 2
GROUP BY 1
ORDER BY 1;

Ссылка на пример с вычислениями

Сведем значения в одну таблицу с помощью CROSS JOIN

Ссылка на пример с вычислениями

Теперь рассчитаем коэффициент Стьюдента.

Ссылка на пример с вычислениями

Следующее, что нам нужно было сделать, посчитать уровень степеней свободы. Оно из себя представляет сумму n1 плюс n2 минус 2. Получаем 18. Теперь нам нужно сравнить соответственно с критическим значением и сделать вывод для уровня значимости 0.05. И критическое значение на пересечении нужного на уровне значимости и степени свободы составляет 2.101.

Теперь давайте подведем небольшой итог. Итак, гипотеза h0. Т-тест не показывает расхождения между выборками, так как тест-статистика, вычисляемая меньше критического. Данные в обеих группах распределены нормально. И возмущение носит случайный характер. Утверждение о том, что данные в обеих группах распределены нормально, мы еще выяснили на прошлом вебинаре. Там мы строили как один из способов доказательства корректности AB-тестирования две гистограммы. И видели, что распределение нормальное.

Альтернативная гипотеза H1 была в том, что тест показывает значительное расхождение между выборками. Это произошло бы, если бы у нас статистика была больше критического. Это обозначало, что данные в обеих группах распределены ненормально, а их возмущение носит зависимый характер.

Мы приняли для наших тестовых данных гипотезу H0 и поняли, что AB-тестирование успешно. То есть мы по сути приняли гипотезу H0.