Множества — Множественные операции в SQL

• Операции над множествами
• Типы объединения таблиц
• Выводы

Работая с IT-системами, мы обычно имеем дело с базами данных, состоящими из большого количества таблиц. Хранить данные в таблицах довольно удобно — по сути, это множества строк. В математике даже есть теория множеств — специальный раздел, который рассматривает различные операции над множествами. В этом уроке мы начнем знакомство с этой темой и базовыми операциями.

Операции над множествами

Сам термин множество обозначает совокупность каких-то элементов. В работе с данными это набор строк, которые возвращает запрос SELECT. В таком случае каждая строка — это элемент множества.

В математике описано много операций, которые можно производить над множествами. Обсудим самые полезные и распространенные. Чтобы лучше понять эти операции, проведем аналогию с операциями на множествах и наглядно покажем их на диаграммах Эйлера.

Для примера рассмотрим два множества:

A = {a,b,c,d}
B = {c,d,e,f}

С ними можно провести три операции. Первая — это объединение. Это просто набор всех элементов двух множеств:

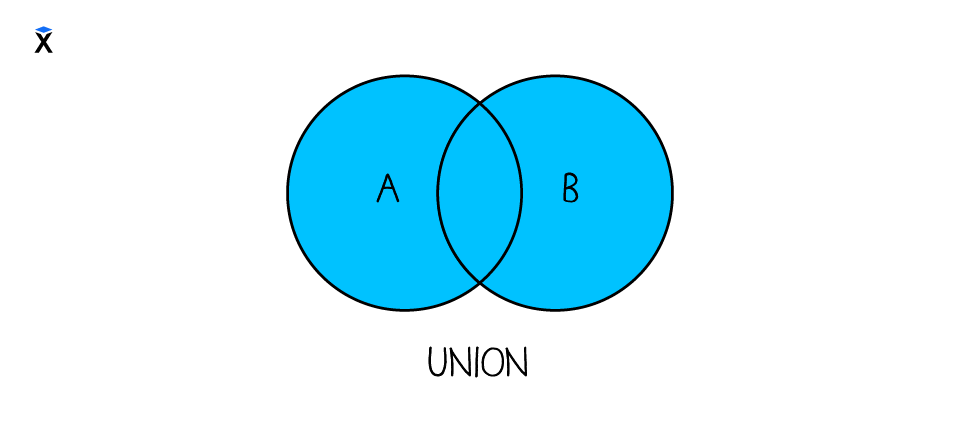
При объединении мы получим набор всех элементов из обоих множеств:

A ∪ B = {a,b,c,d,e,f}

Вторая — это пересечение двух множеств. Так называют поиск общих элементов двух множеств:

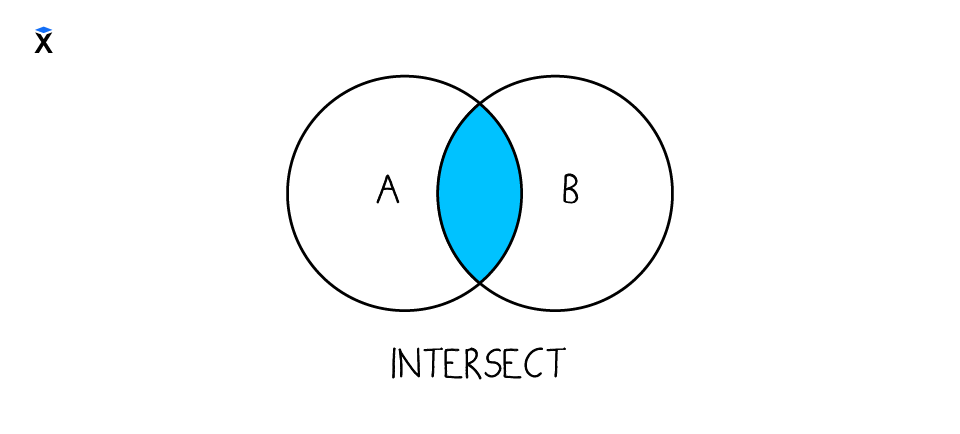
В наших множествах A и B есть два общих элемента — это c и d:

A ∩ B = {c,d}

Третья операция — это разность:

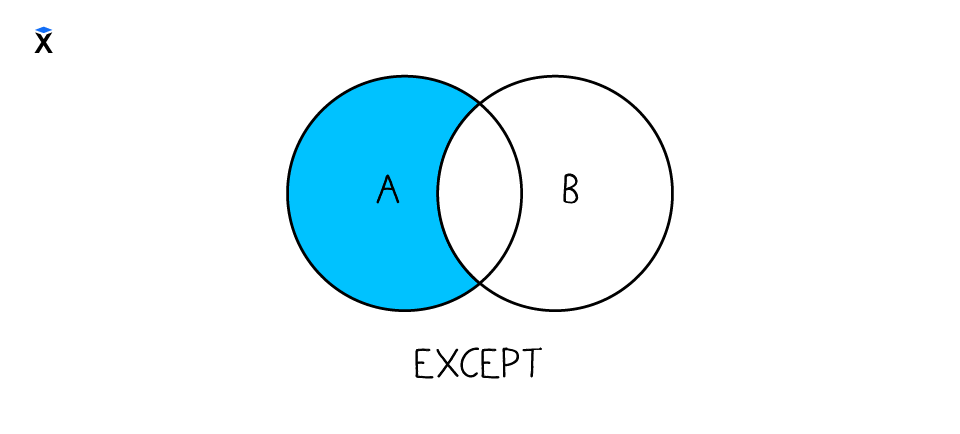
С ее помощью можно найти элементы множества A, которые не встречаются в B:

A \ B = {a,b}

Для всех трех операций в языке SQL существуют специальные операторы. Мы подробно разберем их в этом курсе на практике — мы применим их к этой базе данных.

Типы объединения таблиц

Объединения таблиц можно разбить на два вида. Написав запрос, в обоих случаях мы получаем таблицу, но есть одна важная разница:

Приведем примеры обоих видов на примере двух множеств из начала урока:

A = {a,b,c,d}
B = {c,d,e,f}

Начнем с множественной операции UNION. Если мы ее сделаем, то получим таблицу из всех строк исходных таблиц в неизменном виде. Даже если в двух таблицах были одинаковые строки, в итоговой таблице они будут в единственном экземпляре:

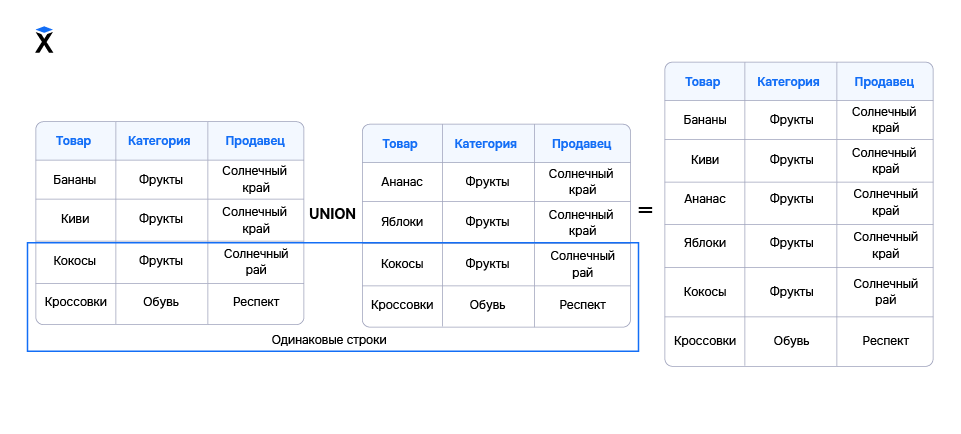
Применив UNION, мы получим объединение A и B, в которое войдут все элементы этих множеств:

A ∪ B = {a,b,c,d,e,f}

Множества A и B удобно визуализировать в виде окружностей:

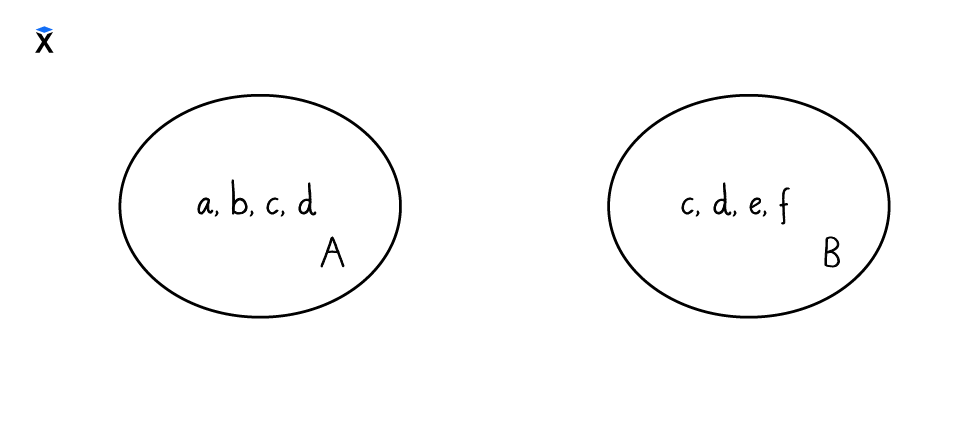
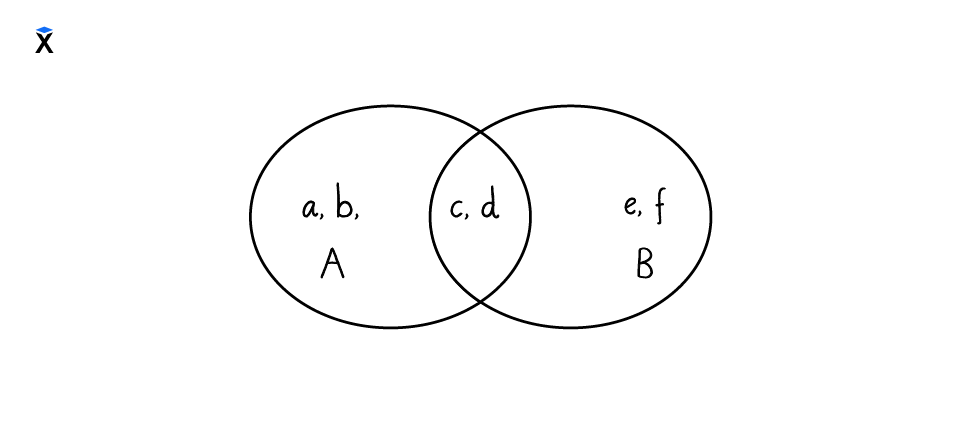
Два множества содержат одинаковые элементы, поэтому можно наложить окружности друг на друга и получить диаграмму Эйлера:

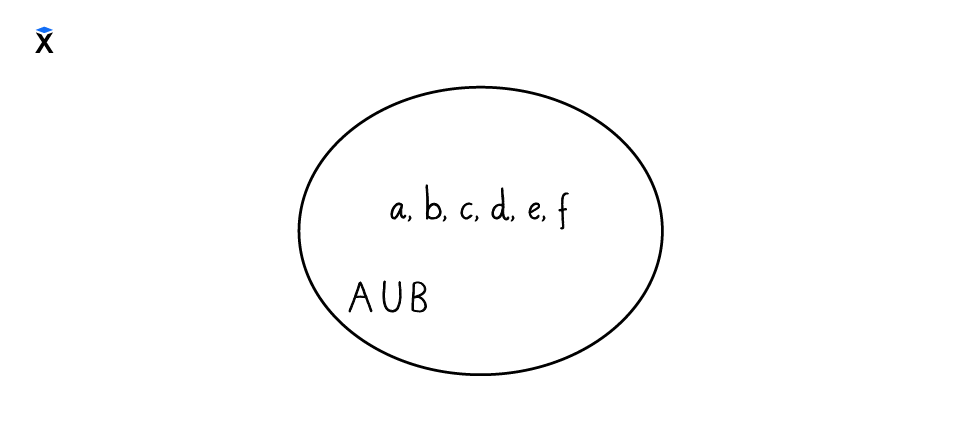
В результате объединения получим множество:

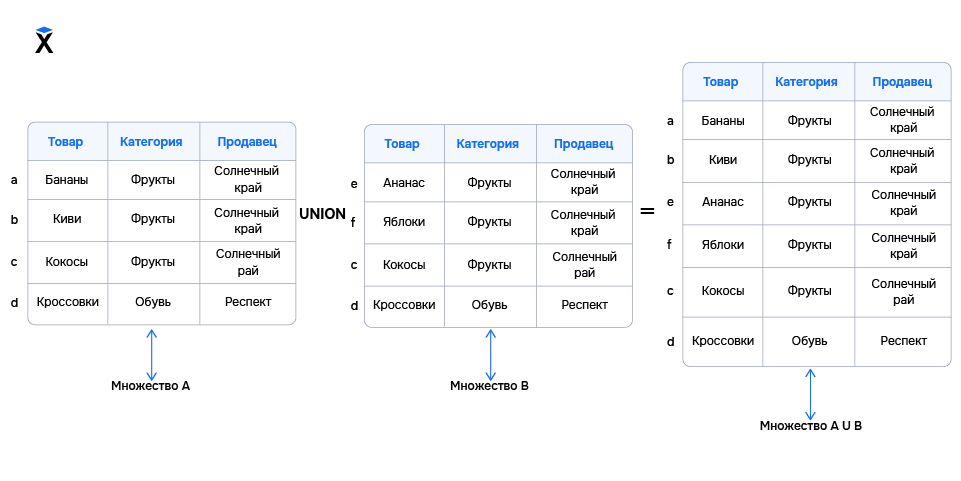
Сопоставим элементы множества со строками в таблице. Так мы подтвердим, что результат операции UNION совпадает с результатом объединения двух множеств:

Приведем пример операции JOIN. Есть две таблицы:

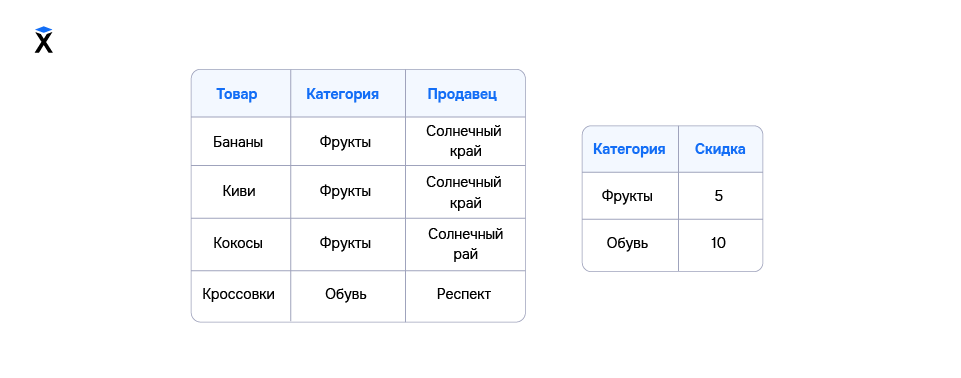
Представим, что нам нужно собрать общую таблицу и добавить информацию о скидке к каждой строчке первой таблицы. В этом случае таблицы связаны столбцом «Категория». Возьмем операцию JOIN и применим ее к столбцу «Категория» этих таблиц. В итоге получим такой результат:

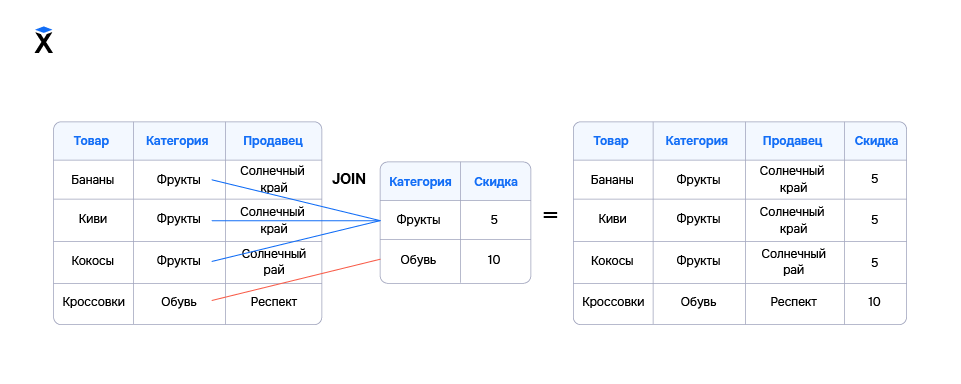
Как видите, мы получили новую таблицу, строки которой отличаются от строк в исходных таблицах. В каждой строке добавилось поле «Скидка», потому что мы сопоставили столбцы «Категория» двух таблиц.

Выводы

В этом уроке мы обсудили два разных вида объединений таблиц и подчеркнули логическую разницу между ними. Пока мы изучили только по одному примеру объединений разных видов. Далее мы разберемся в этой теме подробнее.

Дополнительные материалы

1. Теория множеств: основы и базовые операции над множествами