Ruby: Составные данные
Теория: Рациональные числа
Абстракция
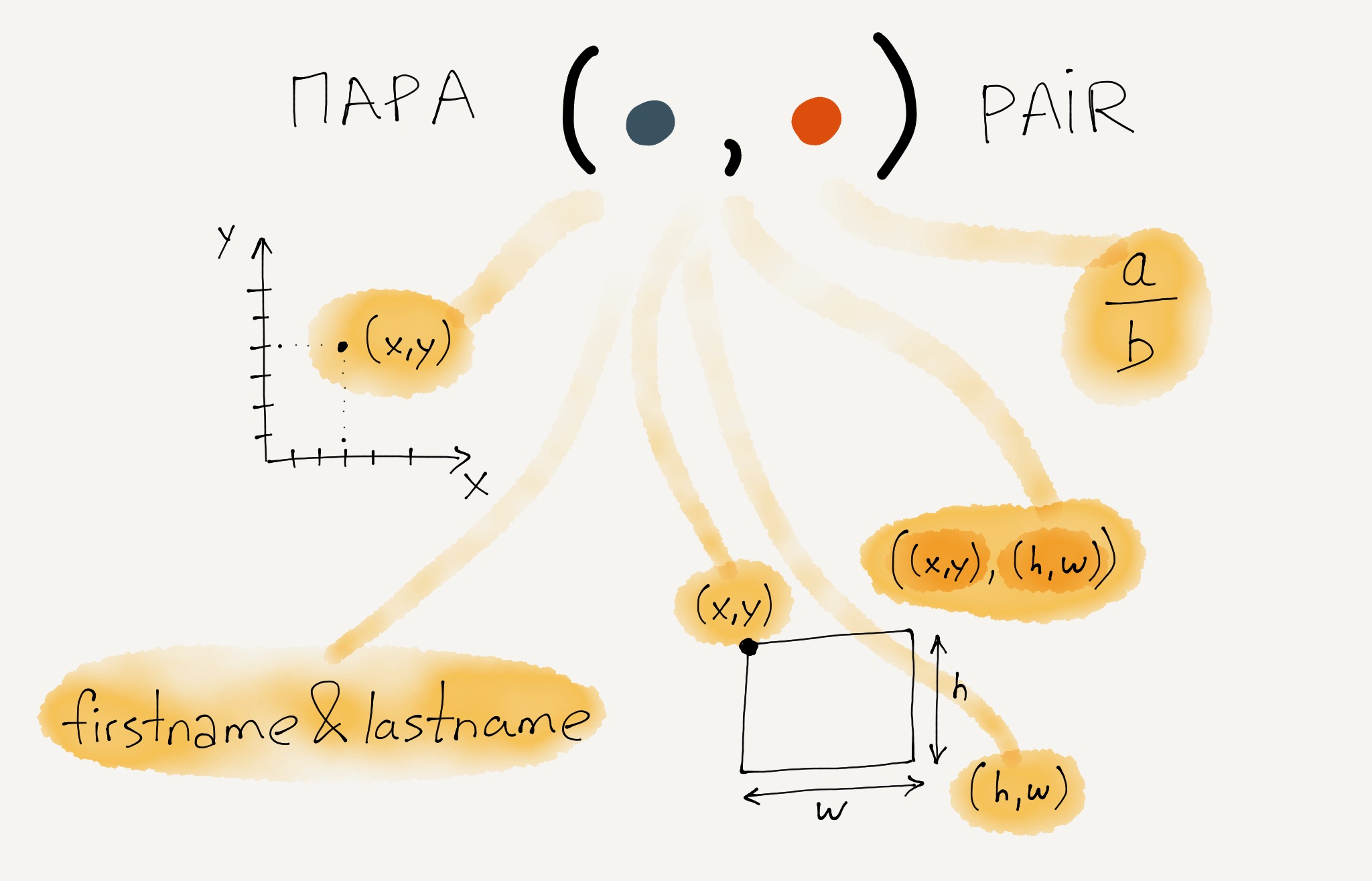
Пары отлично подходят для представления рациональных чисел. Первый элемент пары может выступать числителем, а второй элемент — знаменателем.
a / b → (a, b)
Мы увидели, как пары могут использоваться для представления разных структур, а сочетания таких представлений — создавать новые структуры.
Рациональные числа
Еще одной очень простой и интересной абстракцией, помимо графических примитивов, являются так называемые рациональные числа. С рациональными числами знакомы все. Рациональным называют число, которое можно представить в виде обыкновенной дроби. Обыкновенная дробь состоит из двух чисел — числителя и знаменателя, поэтому эта абстракция идеально ложится на пары. Интерфейс нам уже знаком и состоит из конструктора и двух селекторов:
Конструктор make принимает два числа. Селектор numer ответственен за получение числителя, denom — знаменателя.
На рациональных числах определены различные операции, например, сложение рациональных чисел, умножение — всё это происходит по определённым правилам:
А по такой формуле работает функция is_equal, которая проверяет равенство дробей:
Абстракция позволяет нам делать некоторые интересные вещи так, чтобы остальная часть программы об этом не знала. Например, нормализация дроби:
Сложив два числа из примера, мы получим 5/10, что является одним из представлений числа 1/2 или 10/20 (обычно нормализуют в меньшую сторону). Когда мы говорим про работу с абстракцией, у нас есть несколько способов провести нормализацию числа. Например, это можно делать при вызове конструктора:
Тогда нормализация будет производиться один раз при создании рационального числа. Другой способ — делать нормализацию при вызове селекторов:
При этом снаружи будет совершенно всё равно, какой способ мы используем. Очевидно, что в данном конкретном случае использование первого способа предпочтительней с точки зрения производительности, потому что селекторы будут вызываться намного чаще конструктора, и производить вычисления каждый раз (а они могут быть довольно объёмными) просто неэффективно. Важно понимать на концептуальном уровне, что способ не один, и его выбор зависит от требований к конкретной системе. Поскольку мы построили барьер абстракции, и манипуляции с рациональными числами производятся только через конструктор и селекторы, то оптимизацию можно спокойно отложить на более поздний срок.
Есть ещё один интересный случай — нормализация знака. Например, при создании рационального числа, в котором числитель или знаменатель отрицателен, нам нужно как-то сохранить информацию об этом, чтобы само рациональное число было отрицательным:
Мы можем договориться, что знак хранится в числителе, и потом этот факт везде использовать. Если же отрицательное значение имеет знаменатель, то мы производим нормализацию, перемещая знак в числитель для единообразной работы. Наружу выставляется удобный интерфейс, чтобы пользователю не приходилось задумываться о правильном использовании знака. Всю работу по приведению к нормальной форме мы делаем внутри функции.
При этом есть различные пограничные случаи, например:
В примере выше и числитель и знаменатель в первом рациональном числе — отрицательные числа. В таком случае два знака - у дроби должны уходить. А значит, функция make должна знать об этом. Само по себе это не заработает, и вместо правильного результата могут появляться совершенно непредсказуемые эффекты.
Абстракция данных позволяет нам откладывать момент нормализации до той поры, когда нам действительно понадобится такой функционал. Причём мы можем реализовать его необходимым нам способом. Прикладной код от этого не поменяется — для него реализация значения не имеет.
