Теория: Векторы

Изучая математику, мы сталкиваемся с двумя типами величин:

• Скаляры — величины, которые включают в себя только значение (например, длину, массу, скорость или площадь)
• Векторы — величины, которые включают в себя более одного значения (например, перемещение, ускорение, силу или вес)

В этом уроке мы рассмотрим, что можно представить в виде вектора в математике. Вы узнаете, как векторы помогаю решать системы уравнений и какие базовые математические операции можно проводить с ними.

Что такое вектор

В школьном курсе физики вектор — это такой объект, для полного описания которого необходимы значение и направление. Например, с его помощью можно описать движение велосипедиста: нужно знать, с какой скоростью он движется и в каком направлении.

В математике мы будем работать с немного другим определением вектора. Здесь с помощью вектора можно описать не только движение. Все зависит от системы координат — от пространства, которое мы задаем при решении той или иной задачи.

Представим жилой дом. У него есть ряд характеристик — например, год постройки, количество квартир и цвет. С помощью вектора мы можем охарактеризовать жилой дом набором этих параметров:

• (количество этажей, количество квартир)
• (цвет дома, год постройки, количество подъездов)

Подобные наборы параметров называются векторами*. Характеристики описываемого объекта считаются элементами вектора.

Так выглядит вектор, построенный по этому примеру:

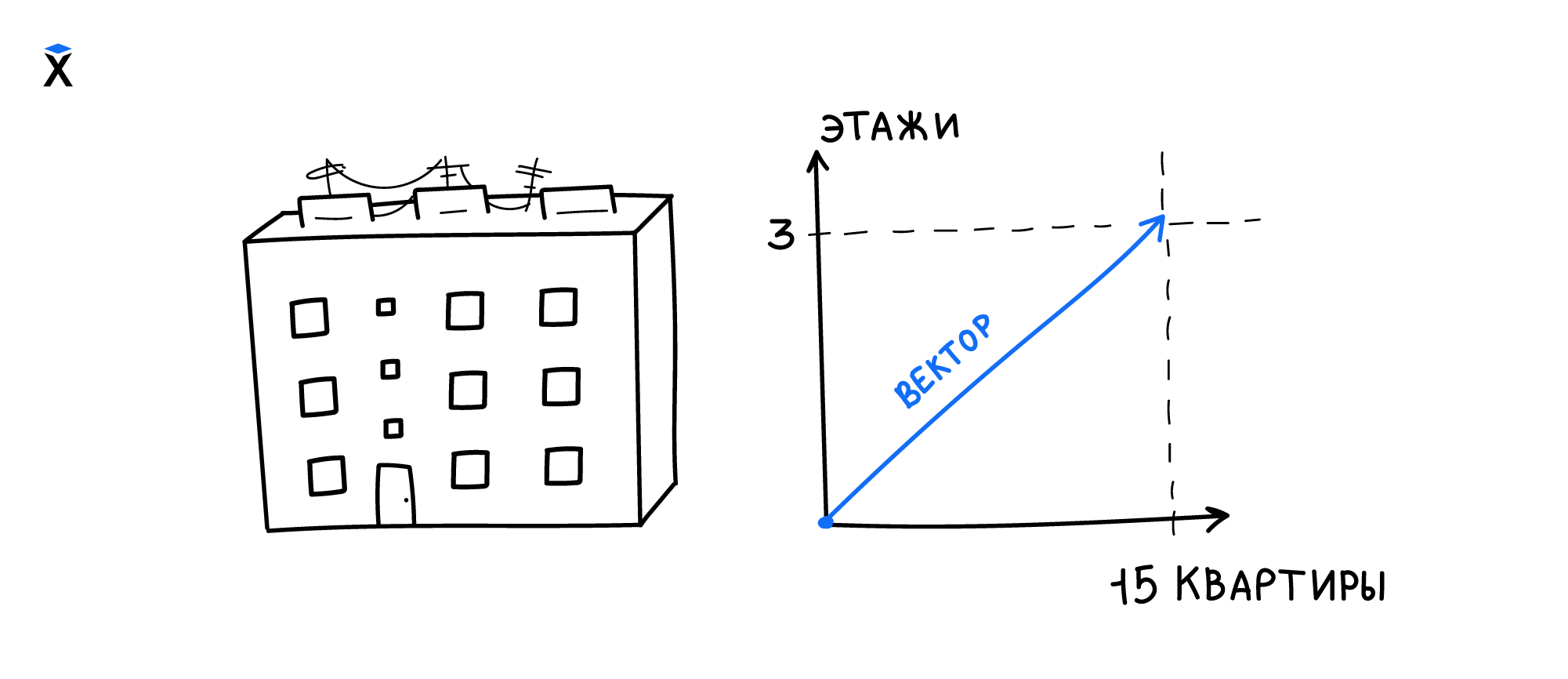
Вектор объединяет несколько характеристик в одну. Получается, с помощью вектора можно обрабатывать данные быстрее и проще.

Векторы обычно представляют в виде символов со стрелкой: v⃗a или v⃗b. В этом курсе мы будем придерживаться такого начертания. На графике векторы изображаются в виде стрелок. Длина стрелки обозначает величину вектора, а угол — направление движения:

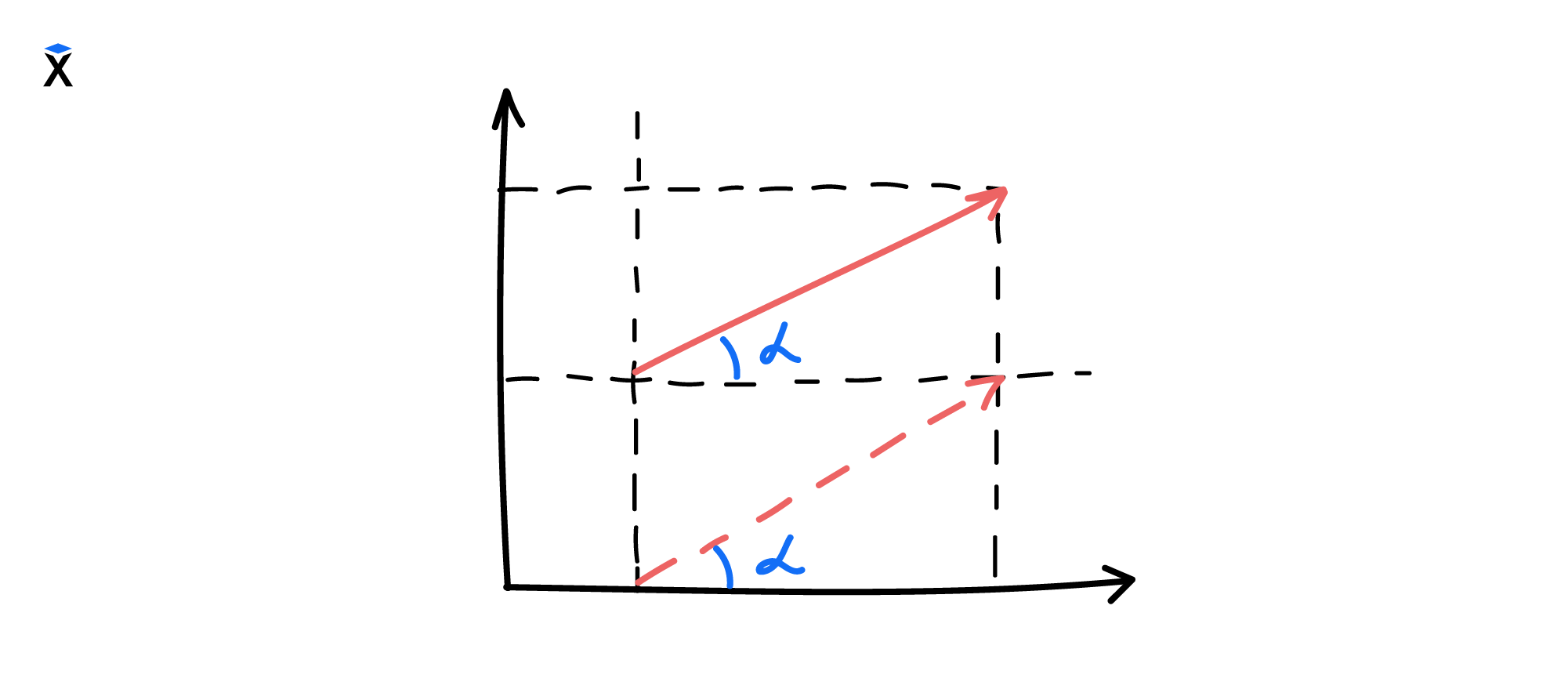
Обратите внимание, что в этом примере векторы не начинаются из начала координат (0,0). В этом нет ничего необычного, потому что вектор может начинаться из любой точки.

Есть несколько способов математического представления векторов, но нам интересно представлять их в виде набора элементов. Попробуем сделать это на примере такого графика:

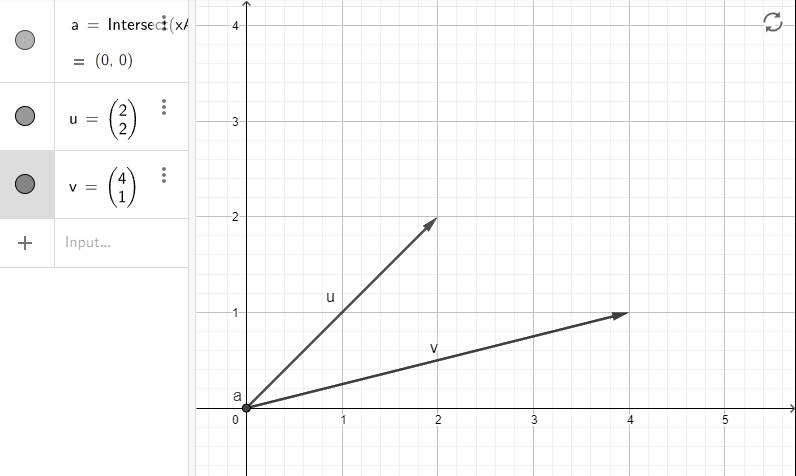
Попробуем математически описать график выше:

• Вектор v⃗u можно представить как (2,2)
• Вектор v⃗v можно представить как (4,1)

Довольно просто представить векторы в двухмерном и трехмерном пространстве, но концепция векторов этим не ограничивается. Именно это делает векторы настолько полезными — например, в машинном обучении.

Возьмем для примера два вектора:

• v⃗c = (2,1,0) в трехмерном пространстве
• v⃗d = (2,1,3,4) в четырехмерном пространстве

Мы не можем показать на графике четырехмерное пространство. Но это не мешает нам проводить операции с векторами в четырехмерном пространстве — все благодаря математическому способу представления векторов. На практике это означает, что можем вшить в вектор столько угодно характеристик.

Именно поэтому векторы находят множество применений в машинном обучении — от построения рекомендательных движков для поисковиков до числового представления слов для обработки естественного языка.

Мы выяснили, что вектор — это набор характеристик. Но вдруг нам нужно добавить характеристику, изменить ее, сравнить один объект с другим? В этом нам помогут математические операции. Начнем с базовых: сложения и вычитания.

Сложение векторов графическим способом

Возьмем те же два вектора v⃗u и v⃗v. Выполним над ними векторное сложение:

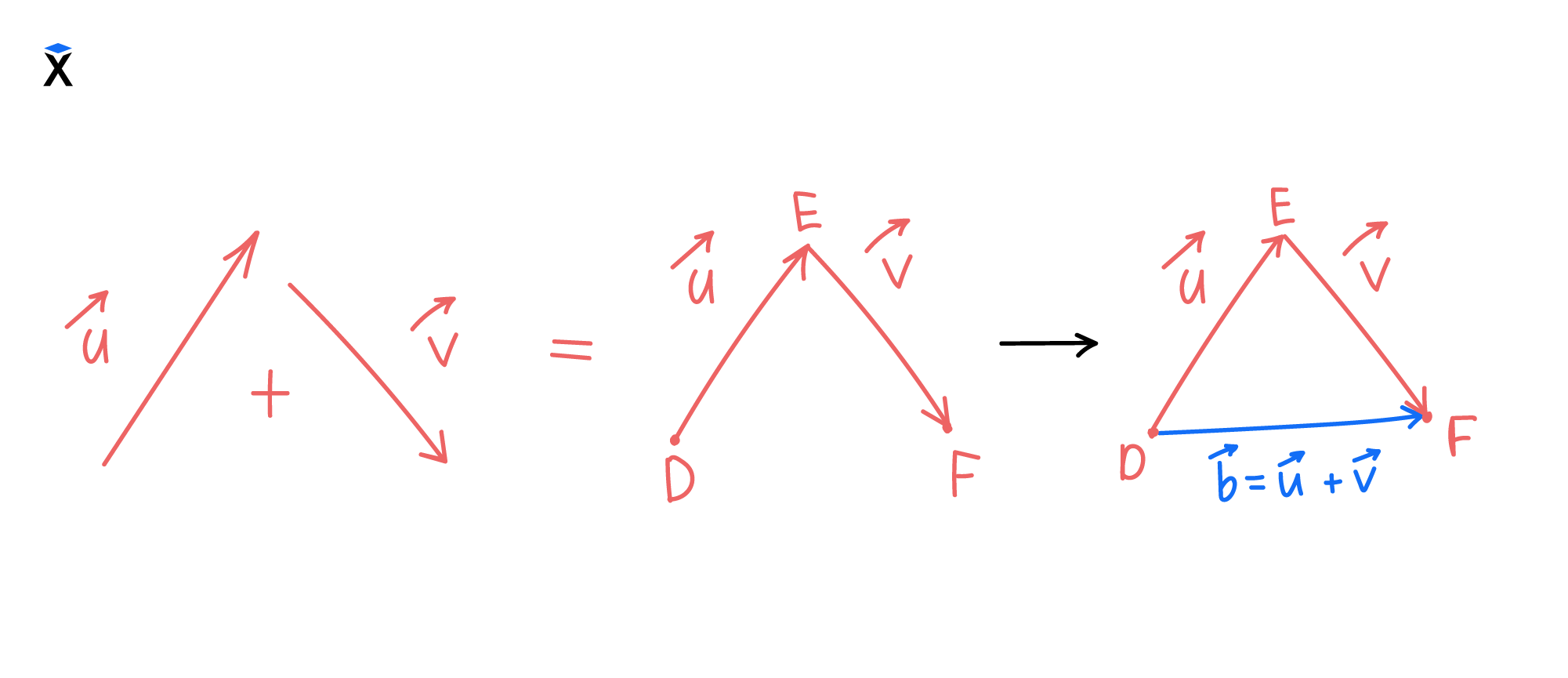
Чтобы графически сложить два вектора v⃗u и v⃗v, мы переместили вектор v⃗v. Мы расположили его так, чтобы его хвост начинался в голове вектора v⃗u (линии DE и EF).

Сумма двух векторов v⃗u и v⃗v — это вектор v⃗b. Он начинается в хвосте v⃗u и заканчивается в голове v⃗v (линия DF).

Чтобы еще лучше понять эту тему, рассмотрим пример из реального мира. Представьте, что вы едете в магазин за продуктами. По дороге вы остановились на заправке. Так эта ситуация будет выглядеть на графике с векторами:

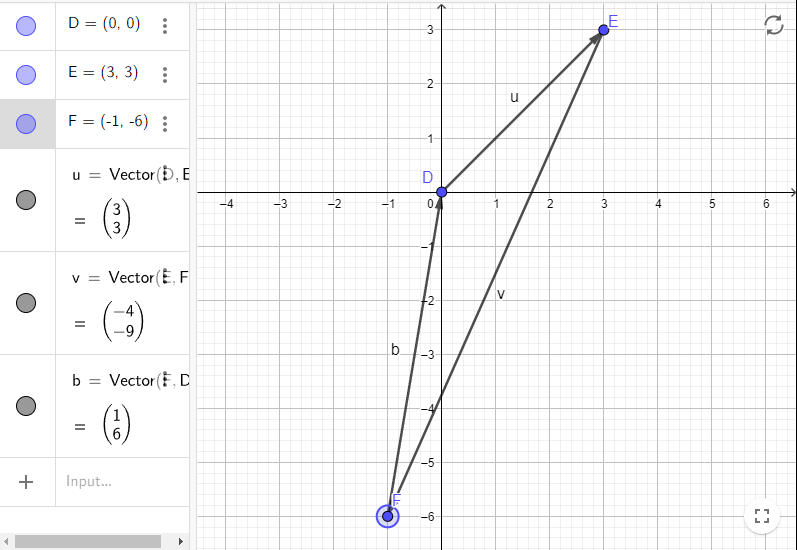
Рассмотрим этот график подробнее. Мы видим три точки:

• D — дом
• E — заправка
• F — магазин

Еще на графике есть два известных вектора:

• v⃗u — расстояние от дома до заправки
• v⃗v — расстояние от заправки до магазина

Нам нужно узнать расстояние от дома до магазина. Для этого мы проводим вектор v⃗b из хвоста v⃗u в голову v⃗v. Таким образом, мы складываем векторы и получаем расстояние между домом и магазином:

v⃗u + v⃗v = v⃗b

Как мы видим на графике, вектор v⃗b можно представить как (1; 6).

Существуют и другие методы вычисления векторного сложения графически — например, метод параллелограмма. Их вы можете изучить самостоятельно.

Сложение векторов математическим способом

Мы можем строить графики каждый раз, когда хотим сложить два вектора, но это работает только с простыми примерами. Если речь идет о четырехмерном пространстве и векторах более высокой размерности, больше подойдет другой способ — математический.

Вернемся к примеру выше:

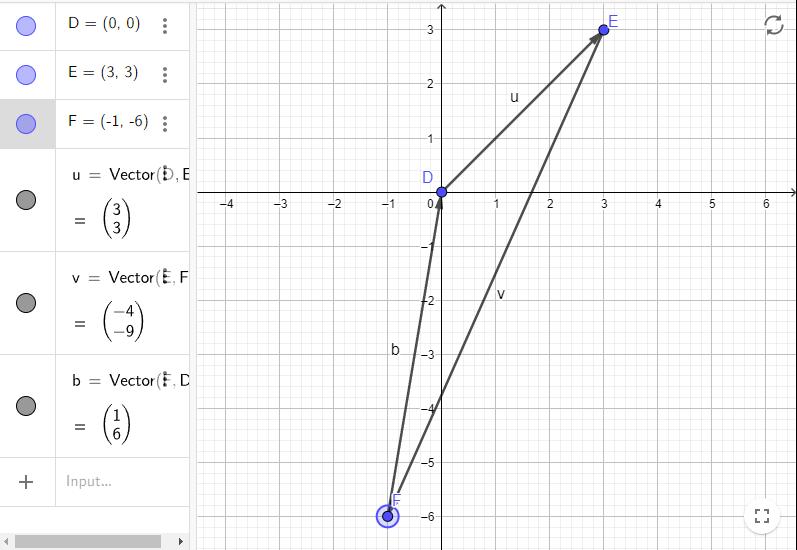
Каждый вектор на этом графике — это набор чисел. Поэтому мы попробуем сложить соответствующие числа каждого вектора. Сначала запишем векторы из примера выше математическим способом:

v⃗u = (3,3)
v⃗v = (-4,-9)

Теперь складываем значения векторов:

• Первое значение из v⃗u с первым значением из v⃗v
• Второе значение из v⃗u со вторым значением из v⃗v

Так мы получаем:

v⃗b = (3 - 4, 3 - 9) = (-1,-6)

Этот ответ совпадает с решением, которые мы уже получили графическим способом. По модулю ответы совпадают, разница только в знаках:

• На графике мы видим вектор со значением (1,6)
• Математически мы получили результат сложения (-1,-6)

Таким образом, сложение векторов можно выполнять простым сложением соответствующих элементов каждого вектора. Как вы уже могли догадаться, складывать можно только векторы с одинаковыми размерами.

Вычитание векторов

Вычитание векторов можно рассматривать как частный случай сложения:

v⃗u - v⃗v = v⃗u + (-v⃗v)

Так выглядит решение графическим способом:

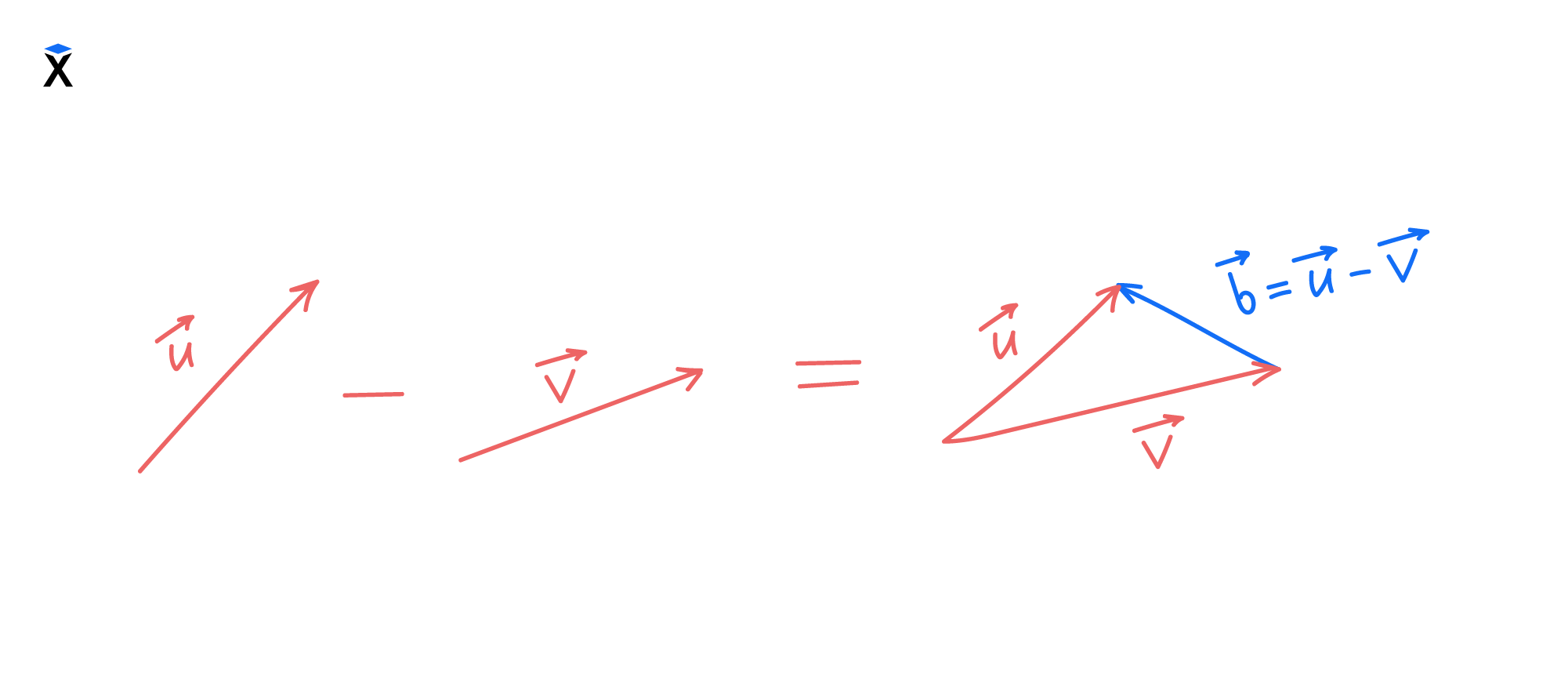
Теперь сделаем это математически, вычитая отдельные компоненты в двух векторах:

v⃗b = v⃗u -v⃗v = (2,2) - (4,1) = (2 - 4, 2 - 1) = (-2,1)

Умножение вектора на скалярное число

Вкратце рассмотрим скалярное умножение — еще одно полезное свойство векторов.

Скаляром называется просто число — это величина, не имеющая направления. Любое целое число является скаляром. Например, рост человека, его год рождения, цена на продукты — все это скалярные величины.

Давайте посмотрим, что произойдет, если мы умножим вектор на скалярную величину. Возьмем такой вектор:

v⃗u = (2,2)

Представим, что нам нужно умножить v⃗u на число 3. Возьмем отдельные числа вектора v⃗u (2,2) и умножим их на 3. Посмотрим, как это будет выглядеть:

3 * v⃗u = (3 * 2, 3 * 2) = (6, 6)

Построим векторы на графике и посмотрим:

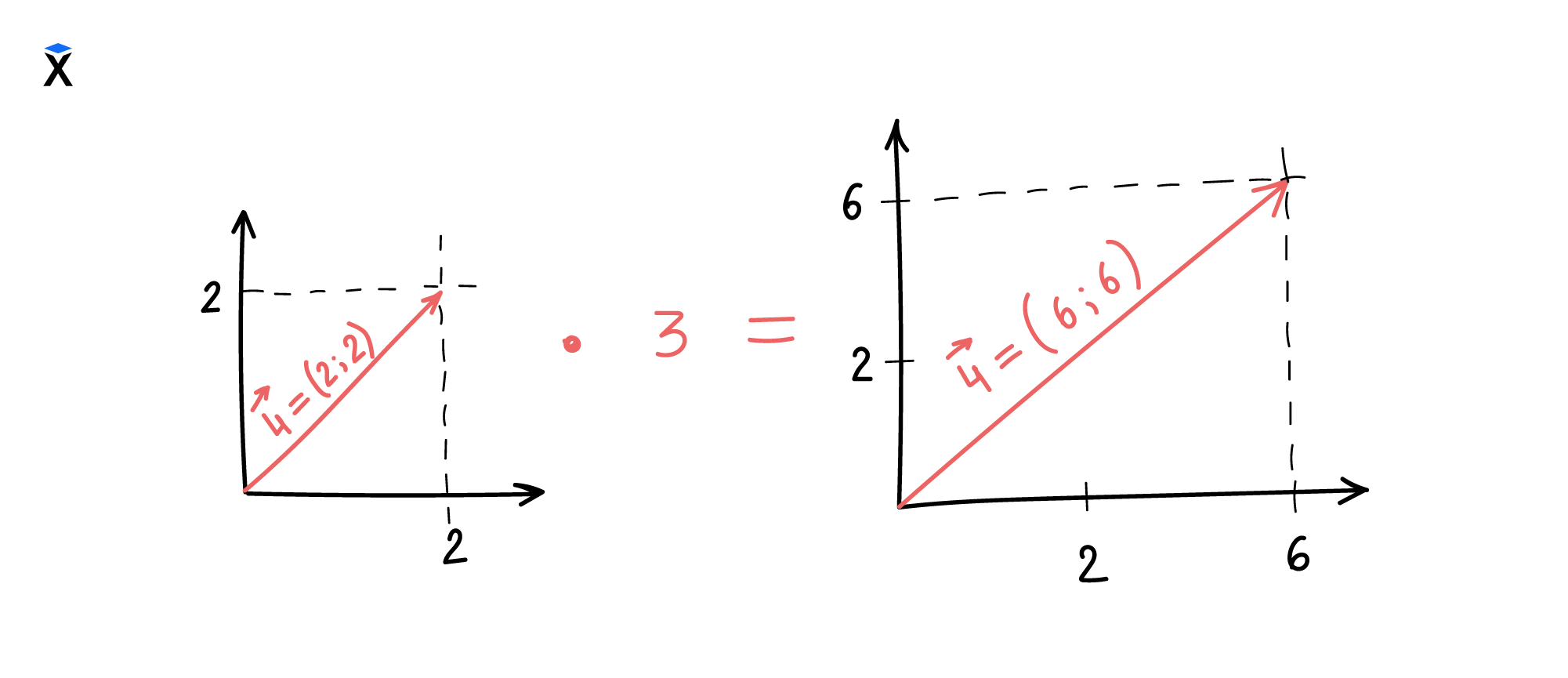
Как видно на графике, при умножении вектора v⃗u на положительное скалярное значение мы получили новый вектор v⃗d. Он имеет то же самое направление, но его величина увеличилась в три раза.

Теперь возьмем другой вектор — v⃗v = (4,1):

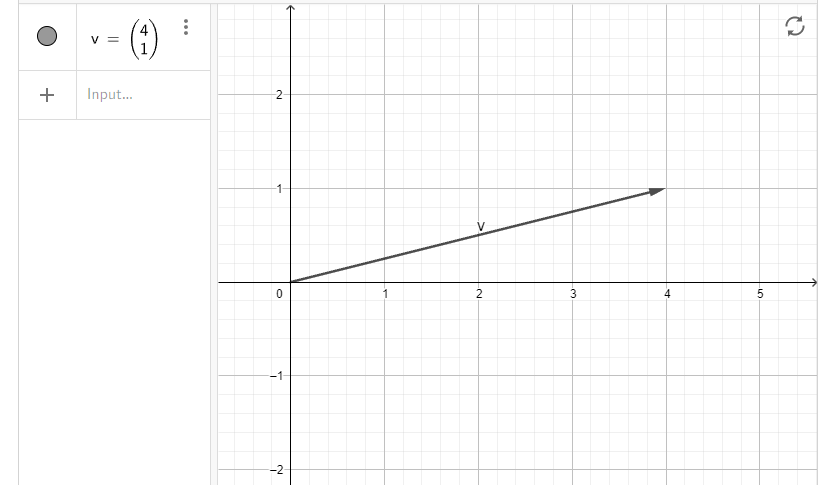
Попробуем умножить его на отрицательное число -1:

-1 * v⃗v = (-1 * 4, -1 * 1) = (-4, -1)

Построим график и посмотрим, как это выглядит:

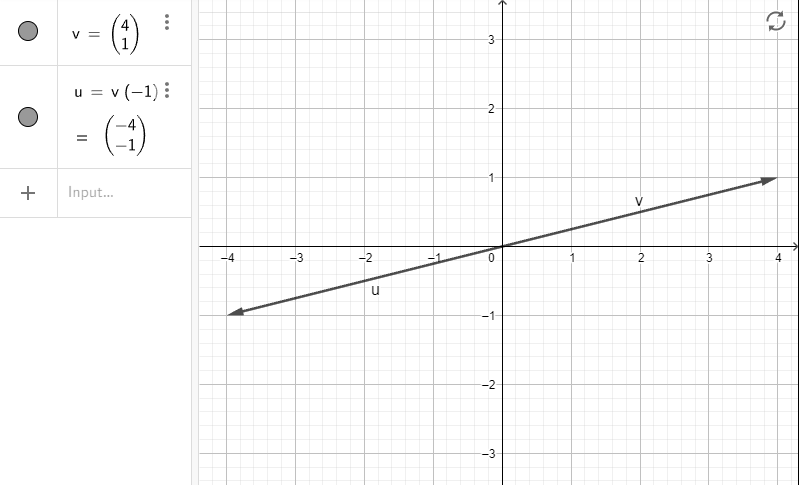
По графику мы видим, что умножение вектора v⃗v на -1 приводит к вектору v⃗e с той же величиной, но противоположного направления. Его можно представить двумя способами:

• v⃗e = -v⃗v
• v⃗e + v⃗v = 0

В этом примере вектор равен нулю, поэтому это нулевой вектор.

Выводы

В этом уроке мы обсудили, чем отличаются скаляры от векторов. Теперь вы знаете, что такое вектор, зачем он нужен и как его обозначать. Еще мы научились проводить базовые операции:

• Сложение и вычитание векторов
• Умножение вектора на скалярное число

В этом уроке мы рассмотрели только самые простые примеры, но на самом деле компоненты вектора можно определить как угодно. Вектор даже может состоять из функций, у компонентов которых тоже будут свои характеристики. Получается матрешка, внутри которой можно хранить огромное количество информации.