Теория: Таблица производных

В этом уроке мы продолжим изучать производные — одно из базовых понятий математики и фундаментальный инструмент для решения многих задач в науке и технике. Вы узнаете больше о типах функций и научитесь работать с таблицей производных, с помощью которой можно решать задачи быстрее и проще.

Определение производной

Производная функции — это показатель ее скорости изменения в точке. Формально производная функции определяется так:

Функция — это предел отношения приращения функции к приращению ее аргумента, когда последнее стремится к нулю. При этом важно помнить, что производная функции не всегда существует в каждой точке. Она может не существовать на границах определения функции или в точках, где функция имеет разрывы

Типы функций и их производные

Существуют различные типы функций, для которых можно найти производную:

• Константная. К этому типу функция, значение которой не зависит от аргумента. Например, $f(x)$ считается константной функцией, если ее значение не зависит от аргумента $x$. Производная такой функции всегда равна нулю
• Линейная. Это функция с постоянными коэффициентами $k$ и $b$, которая имеет вид $f(x) = kx + b$. Производная такой функции равна $f'(x) = k$
• Степенная. Это функция с целым числом $n$, которая имеет вид $f(x) = x^n$. Ее производная равна $f'(x) = nx^{n-1}$
• Экспоненциальная. Это функция с постоянным числом $a$, которое при этом больше нуля. Она имеет вид $f(x) = a^x$. Производная равна $f'(x) = a^x * \ln \a$. Другими словами, чтобы найти производную, нужно умножить константу на функцию
• Логарифмическая. Это функция $f(x) = \ln \x$. Ее производная равна $f'(x) = \frac{1}{x}$

Чтобы формулы лучше запомнились, соберем их в таблицу:

|====

| Тип функции | Функция | Производная | Примечание

| Константная | $f(x)=k$ | $f'(x) =0$ | $k$ — постоянный коэффициент

| Линейная | $f(x) = kx + b$ | $f'(x) = k$ | $k$ и $b$ — постоянные коэффициенты

| Степенная | $f(x) = x^n$ | $f'(x) = nx^{n-1}$ | $n$ — целое число

| Экспоненциальная | $f(x) = a^x$ | $f'(x) = a^x * \ln \a$ | $a$ — постоянное число больше нуля

| Логарифмическая | $f(x) = \ln \x$ | $f'(x) = \frac{1}{x}$ | |====

Тригонометрические функции

Тригонометрические функции — это функции, которые определяются через соотношения между сторонами прямоугольного треугольника:

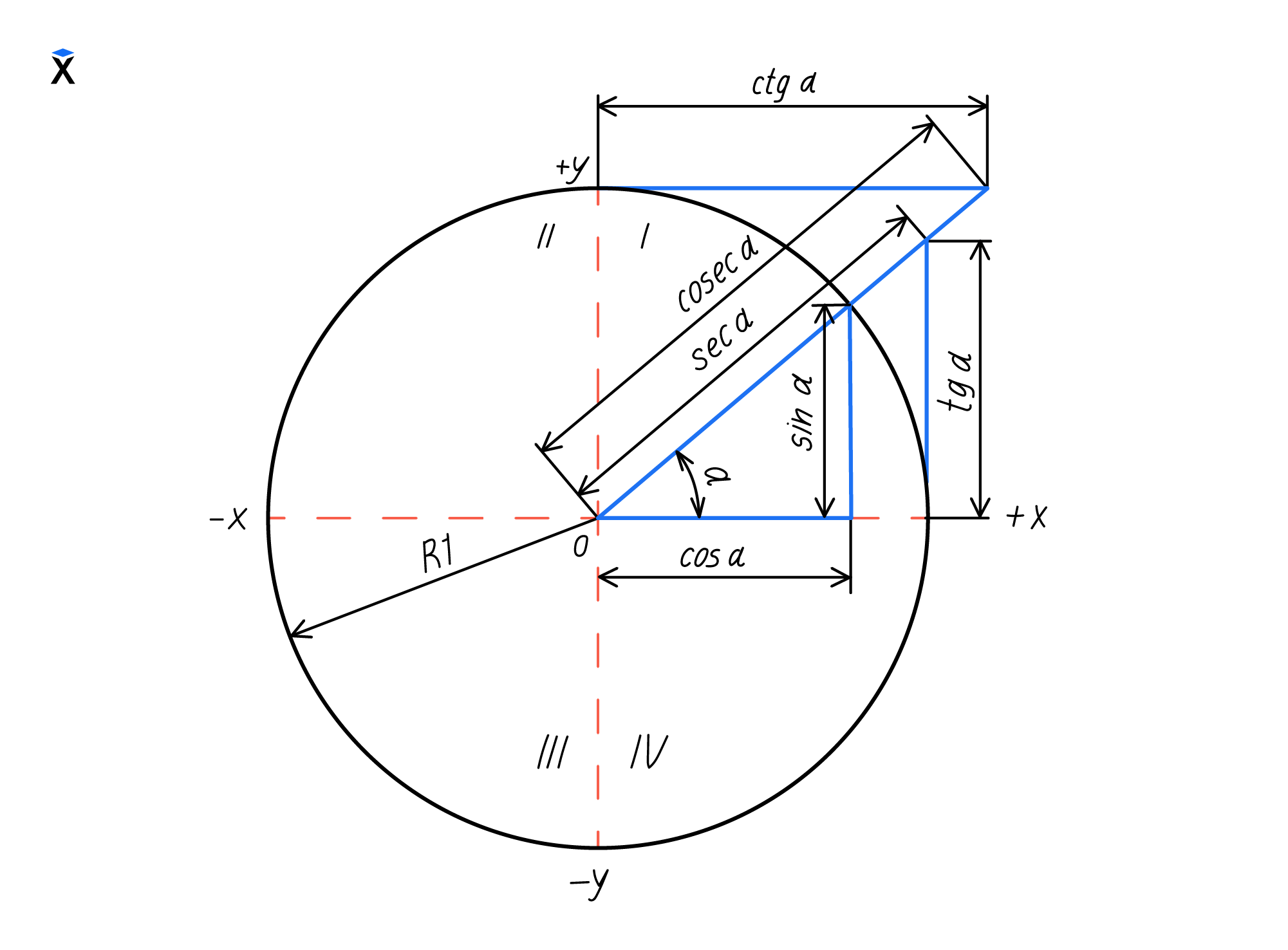
Рассмотрим самые распространенные тригонометрические функции:

|====

| Функция | Производная | Описание

| $f(x) = \frac{d}{dx}\sin x$ | $f'(x) = \cos x$ | Производная синуса равна косинусу

| $f(x) = \frac{d}{dx}\cos x$ | $f'(x) = -\sin x$ | Производная косинуса равна минус синусу

| $f(x) = \frac{d}{dx}\tan x$ | $f'(x) = \sec^2 x$ | Производная тангенса равна квадрату секанса

| $f(x) = \frac{d}{dx}\cot x$ | $f'(x) = -\csc^2 x$ | Производная котангенса равна минус квадрату косеканса

|====

Обратные тригонометрические функции

Обратные тригонометрические функции — это функции, которые позволяют находить углы, соответствующие заданным значениям тригонометрических функций. Снова составим таблицу с самыми распространенными обратными тригонометрическими функциями:

|====

| Название | Функция | Производная

| Арксинус | $f(x) = \arcsin x$ | $f'(x) = \frac{1}{\sqrt{1-x^2}}$

| Арккосинус | $f(x) = \arccos x$ | $f'(x) = -\frac{1}{\sqrt{1-x^2}}$

| Арктангенс | $f(x) = \arctan x$ | $f'(x) = \frac{1}{1+x^2}$

| Арккотангенс | $f(x) =arc\cot x$ | $f'(x) = -\frac{1}{1+x^2}$ |====

Таблица производных

В таблице ниже мы приводим производные основных функций, а также некоторых комбинаций функций. В этой таблице:

• $a$ — постоянное число
• $n$ — целое число
• $f(x)$ и $g(x)$ — функцииs
• $x$ — независимая переменная

Рассмотрим сами формулы.

Производные основных функций

|====

| Функция $f(x)$ | Производная $f'(x)$

| $k$ | $0$

| $x$ | $1$

| $x^n$ | $n * x^{n-1}$

| $e^x$ | $e^x$

| $a^x$ | $a^x * \ln a$

| $\ln x$ | $\frac{1}{x}$

|====

Производные комбинаций функций

Производные тригонометрических функций

|====

| Функция $f(x)$ | Производная $f'(x)$

| $\sin x$ | $\cos x$

| $\cos x$ | $-\sin x$

| $\tan x$ | $\sec^2 x$

| $\cot x$ | $-\csc^2 x$

| $\arcsin x$ | $\frac{1}{\sqrt{1-x^2}}$

| $\arccos x$ | $-\frac{1}{\sqrt{1-x^2}}$

| $\arctan x$ | $\frac{1}{1+x^2}$

|====

Некоторые производные можно вывести из других при помощи правил дифференцирования. Например, производную функции $\log_a x$ можно вывести из производной функции $\ln \x$, используя замену переменных.

Как использовать таблицу производных

Попробуем воспользоваться таблицей производных. Для этого нужно сделать три шага:

• Определяем тип функции, для которой требуется найти производную. Например, это может быть степенная, тригонометрическая или логарифмическая функция
• Из таблицы находим формулу для производной функции данного типа
• Подставляем значения переменных в формулу и вычисляем производную

Для примера представим, что нам нужно найти производную функции $f(x) = \cos x$. Проговорим порядок действий:

• Определяем тип — тригонометрическая функция, потому что речь идет о косинусе
• Ищем в таблице производных формулу для производной косинуса: $\frac{d}{dx}\cos x = -\sin x$
• Подставляем $x$ в формулу и получаем производную: $f'(x) = -\sin x$

Виды производных

Есть несколько видов производных, которые могут быть полезны для решения различных задач:

• Первая производная — показывает скорость изменения значения функции в каждой точке
• Вторая производная — показывает, как изменяется скорость изменения значения функции в каждой точке
• Частные производные — используются в многомерном анализе и показывают, как функция изменяется в зависимости от изменения каждого из ее аргументов

Как работать с производными на практике

Знание о типах функций и знакомство с таблицей производных не научит работать с функциями. Навык придет со временем и регулярной практикой.

Чтобы лучше понять тему урока, рассмотрим несколько примеров.

Пример 1

Возьмем первую задачу — найти производную в точке $x = 1$ от функции $f(x) = 2x^3 + 5x^2 - 3x + 2$.

Для вычисления производной функции, мы должны найти производную каждого члена функции, а затем сложить их вместе. Каждый член функции — это многочлен.

Попробуем вычислить производную многочлена. Сначала мы умножаем каждый член многочлена на его степень, а затем уменьшаем степень уменьшается на единицу. Применяя это правило к каждому члену функции, получаем:

• Производная первого члена $6x^2$
• Производная второго члена $10x$
• Производная третьего члена $3$
• Производная четвертого члена $0$ (производная константы равна нулю)

Затем мы просто складываем все производные членов функции вместе, чтобы получить итоговую производную:

$f'(x) = 6x^2 + 10x - 3$

Таким образом, производная функции $f(x) = 2x^3 + 5x^2 - 3x + 2$ равна:

$f'(x) = 6x^2 + 10x - 3$.

Далее мы находим производную для $x=1$:

$f'(1) = 61^2 + 101 - 3 = 13$

Пример 2

Во второй задаче попробуем найти производную функции $f(x) = \sin^2 x + \cos^2 x$.

Сначала мы используем тригонометрическое тождество $\sin^2 x + \cos^2 x = 1$, чтобы упростить функцию $f(x)$:

$f(x) = \sin^2 x + \cos^2 x = 1$

Теперь мы можем найти производную этой функции, используя производные элементарных функций и правила дифференцирования сложной функции. Для этого мы берем производную каждого слагаемого по отдельности и складываем:

$f'(x) = (\sin^2 x)' + (\cos^2 x)' = 2\sin x \cos x - 2\cos x \sin x = 0$

Здесь мы использовали производные элементарных тригонометрических функций и правило дифференцирования произведения функций. Как мы видим, производная функции $f(x)$ равна нулю.

Так мы выяснили, что производная функции $f(x) = \sin^2 x + \cos^2 x$ равна нулю. Это означает, что функция постоянна — то есть она не изменить свое значение, если мы поменяем аргумент.

Если упростить, то решение задачи выглядит так:

$f'(x) = 2\sin x * \cos x - 2\cos x * \sin x = 0$

Пример 3

В качестве еще одной задачи найдем производную функции $f(x) = e^{3x} * \ln \x$.

Для начала найдем производную функции $f(x) = e^{3x} * \ln \x$. Применим правило производной произведения:

$f'(x) = (e^{3x} * \ln \x)' = (e^{3x})' * \ln \x + e^{3x} * (\ln \x)'$

И правило производной логарифма:

$= 3e^{3x} * \ln \x + e^{3x} * \frac{1}{x}$

В итоге мы получаем:

$f'(x) = 3e^{3x} * \ln \x + e^{3x} * \frac{1}{x}$

Выводы

В этом уроке мы познакомились с таблицей производных, которая поможет быстрее работать с функциями на практике.

Теперь вы знаете, как с помощью таблицы быстро найти производную для большинства функций. Для этого нужно определить тип функции и подставить значения переменных в соответствующую формулу для производной из таблицы.

Кроме того, таблица производных может быть полезной для решения задач физики и других наук. Например, производная функции показывает скорость изменения положения тела в пространстве или скорость изменения силы, действующей на материальную точку.