Теория: Производная в математике

Производные — это одно из фундаментальных понятий математического анализа. Они помогают работать с векторными функциями и показывают, как изменяется функция в каждой точке графика.

Знание производных полезно не только математикам, но и программистам в области машинного обучения, аналитикам данных, физикам, экономистам, социологам и всем специалистам, которые изучают изменение параметров во времени.

Что такое производная

Производная — это показатель изменения функции в каждой точке графика. Значение производной в каждой точке равно скорости изменения функции в этой точке. Другими словами, производная показывает, как меняется значение функции в каждой точке графика.

В формулах производная обозначается вот таким образом:

• Сама функция — $f(x)$
• Ее производная — $f'(x)$

Рассмотрим еще несколько примеров:

Производная может показывать возрастание и убывание:

• Если производная положительна, то функция возрастает в данной точке
• Если производная отрицательна, то функция убывает в данной точке
• Если производная равна нулю, то функция в этой точке имеет экстремум — максимум или минимум

Еще производные бывают разных порядков. Они используются для разных задач:

• Производная первого порядка показывает, с какой скоростью меняется функция в каждой точке графика
• Производная второго порядка показывает, с какой скоростью функция меняется не в точках, а в целом. С помощью такой функции можно определять выпуклость или вогнутость кривой в конкретной точке
• Производные более высоких порядков помогают определить форму кривой

Как находить производные

Есть несколько методов нахождения производных функций. Рассмотрим некоторые из них.

Дифференцирование по формулам

С помощью этого метода можно найти производную элементарной функции — то есть функции, которая выражена в виде конечной комбинации элементарных функций (степеней, тригонометрических функций, экспоненты, логарифма и так далее).

Производную элементарной функции можно найти с помощью таких формул:

• (x^n)' = nx^(n-1)
• (sin x)' = cos x
• (cos x)' = -sin x
• (tan x)' = sec^2 x
• (e^x)' = e^x
• (ln x)' = 1 / x

Дифференцирование сложной функции

С помощью этого метода можно найти производную сложной функции — то есть функции, состоящей из нескольких функций, связанных друг с другом.

Формула для нахождения производной сложной функции выглядит так:

(f(g(x)))' = f'(g(x)) * g'(x), где f и g — это две разные функции

Дифференцирование по определению

Этим методом можно пользоваться при работе с любой функцией. Чтобы найти производную по этому методу, нужно применить формулу:

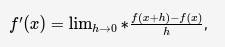
где h — это очень маленькое число

Как находить производные разными методами

Описанные выше способы можно сочетать между собой. Другими словами, в большинстве случаев одну и ту же производную можно найти двумя разными путями.

Дифференцирование по формулам и определению

Для примера представим, что нам нужно найти производную функции f(x) = x^2 + 2x.

Это можно сделать двумя путями. Для начала рассмотрим более простой путь — дифференцирование по формулам:

f'(x) = (x^2)' + (2x)' = 2x + 2 = 2(x+1)

Так же можно применить дифференцирование по определению:

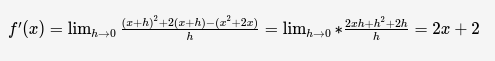
Дифференцирование сложной функции и по определению

Возьмем другой пример и найдем производную функции f(x) = sin x^2.

Здесь тоже есть два способа. Первый — дифференцирование сложной функции:

f'(x) = cos x^2 * (x^2)' = 2x * cos x^2

Второй метод — дифференцирование по определению:

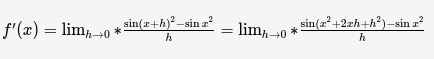
Применяя формулу для разности синусов, получаем:

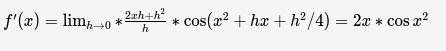
Выводы

В уроке мы познакомились с производной и методами ее нахождения. Это важная задача в математике, которая находит свое применение в различных областях. Далее в курсе мы продолжим изучать производные и принципы работы с ними.