Функции
Теория: Обратные функции
В этом уроке мы узнаем об обратных функциях. Мы разберем, что такое обратная функция и как ее найти.
Такие функции нужны для решения уравнений типа y=f(x). Например, уравнение cos(x) =1/3 можно решить только таким образом.
Что такое обратная функция
Для начала скажем, что обратной называют функцию, которая может превратиться в другую функцию. Проще говоря, если любая функция f переводит x в y, то обратная f переведет y в x.
Если функция обозначается f или F, то обратная функция обозначается f^(-1) или F^(-1). Здесь не следует путать -1 с экспонентой или взаимно обратным показателем.
Формальное определение будет звучать так:
Если f и g — обратные функции, то f(x) = y тогда и только тогда, когда g(y) = x
Обратная функция часто используется в математике — например, в тригонометрии. С ее помощью можно найти меру угла, для которого функция синуса дала значение. Так это выглядит:
sin^(-1)(1) = sin^(-1)(sin 90) = 90 градусов
Следовательно, sin 90 градусов равен 1
Как определить обратную функцию
Обычная функция принимает значения, выполняет определенные операции над этими значениями и выдает результат.
Обратная функция согласуется с результирующей, выполняет операции и возвращается к исходной функции. Обратная функция возвращает исходное значение, для которого функция дала выход.
Если рассматривать функции, то f и g считаются обратными:
f(g(x)) = g(f(x)) = x
Функция, состоящая из своих обратных, возвращает исходное значение. Так это выглядит на практике:
f(x) = 2x + 5 = y
В таком случае g(y) = (y-5)/2 = x является обратной функцией f(x).
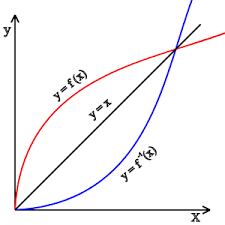
Как строить график обратной функции
График обратной функции отражает две вещи:
- Сама функция
- Обратная функция, проведенная через линию
y = x
Эта линия на графике проходит через начало координат и имеет наклон 1. Она может быть представлена как:
y = f^(-1)(x)
Выражение выше равносильно такому выражению:
x = f(y)
Это соотношение немного похоже на y = f(x), которое определяет график f. Но обратите внимание на разницу — части x и y поменялись местами. Поэтому если нам нужно построить график f^(-1), то мы должны поменять местами оси x и y.
Когда мы создаем обратную функцию от исходной, меняется и область на графике. Область исходной функции становится областью обратной функции, а область заданной функции становится областью обратной функции.
График обратной функции получается так: нужно взять исходный график и заменить его координаты (x, y) на (y, x) относительно прямой y = x.
Переход от функции к обратной функции выглядит так:
f^(-1)(f o f^(-1)) (x) = (f^(-1) o f) (x) = x
Чтобы функция f считалась обратной функцией, каждый элемент в диапазоне y в Y должен быть отображен из некоторого элемента x в X в доменное множество. Такое отношение называется отношением один-один или отношением запрета.
Также обратная функция f^(-1) данной функции имеет область y в Y, связанную с отдельным элементом x в X в кодоменном множестве. Такое отношение по отношению к данной функции f является онто-функцией или сюръекцией.
А еще существуют биективные функции — так называют обратные функции, которые являются инъюнктивными и сюръективными.
Что такое инверсия функций
Если в результате композиции двух функций f(x) и g(x) получается тождественная функция f(g(x))= x, то говорят, что эти две функции являются инверсиями друг друга.
Если применение функции x к входу дает n выход y, то применение другой функции g к y должно вернуть значение x. Следовательно, обратная функция обращает функцию. Область данной функции становится областью обратной функции, а область данной функции становится областью обратной функции.
В общем, обратная функция — это отражение функции начала координат относительно прямой y = x. Ее можно получить, заменив (x, y) на (y, x).
Если даны графики двух функций, можно определить, являются ли они обратными друг другу. Если графики обеих функций симметричны относительно прямой y = x, то мы говорим, что эти две функции являются обратными друг другу. Это объясняется тем, что если (x, y) лежит на функции, то (y, x) лежит на ее обратной функции:
Обратная функция — это любая функция, которая никогда не принимает одно и то же значение дважды. Другими словами, для каждого значения x существует только одно значение y. Это означает, что каждый элемент кодомена является образом не более чем одного элемента его области.
Кроме того, обратная функция проходит тесты на вертикальную линию и горизонтальную линию:
Никакая горизонтальная линия не пересекает ее график более одного раза. Таким образом, никакие два элемента в домене не соответствуют одному и тому же элементу в диапазоне
Как найти обратную функцию
Разберемся, как находить обратную функцию. Для этого мы возьмем такой пример:
f(x) = ax + b
Пройдем весь процесс по шагам.
Шаг 1. Возьмем заданную функцию f(x) = ax + b и заменим в ней f(x) на y. Так мы получим такое выражение:
y = ax + b
Шаг 2. Далее возьмем функцию y = ax + b. В ней мы заменим x на y, а y — на x. Получится такое выражение:
x = ay + b
Шаг 3. Далее попробуем решить выражение x = ay + b для y. На этом шаге мы получим:
y = (x - b/a)
Шаг 4. В конце заменяем y на f^(-1)(x). В итоге получаем такой результат:
f^(-1)(x) = (x - b)/a
