Теория: Связный список

В этом уроке мы начнем изучать структуры данных и связанные с ними алгоритмы. Чтобы разобраться во всех деталях, мы рассмотрим два примера из реальной жизни — склад и библиотеку.

На складе кладовщик записывает все пришедшие товары в специальный журнал. Рабочий день кладовщика состоит из приема и выдачи товаров. Очень важно записывать прием и выдачу как можно быстрее, поэтому кладовщик просто пишет все операции друг за другом, подряд.

Из-за специфики работы склада кладовщик составляет базу данных, в которой:

• Сложно найти товар на складе
• Просто сделать новую запись в журнале

Ситуация в библиотеке совсем другая. Основная работа библиотекаря — поиск книг по фамилии автора, по названию книги или по тематике. Для быстрого поиска книг библиотекари используют картотеку. Для каждой книги заводятся несколько карточек и размещаются в разных ящиках. В одном они упорядочены по фамилии автора, в другом — по названию. Благодаря порядку карточки ищутся очень быстро.

Так в библиотеке составляется база данных с совсем другими свойствами:

• Просто найти книгу в библиотеке
• Сложно сделать новую запись в картотеке

И на складе, и в библиотеке нам приходится записывать и искать похожую информацию, однако скорость записи и поиска получается разная:

Как видите, мы не можем выбрать один универсальный способ записи, который подойдет для всех случаев. Для склада больше подходит Журнал, а для библиотеки — Картотека.

В обоих примерах своя структура данных — то есть способ хранения данных в памяти компьютера. Для каждой структуры существует набор основных операций — добавление, поиск, удаление. Из-за особенностей структуры, добавление и поиск могут быть быстрыми или медленными.

Программисты изучают основные структуры данных и запоминают скорость основных операций. Это помогает им выбирать самые подходящие структуры для решения задач пользователя. В этом уроке мы познакомимся со связным списком и сравним его с массивом.

Как устроен массив

Чтобы освоиться с понятием структуры данных и ее операциями, давайте исследуем структуру, которая нам хорошо известна — массив.

В JavaScript все данные относятся к примитивным или ссылочных типам. Числа и булевы значения хранятся непосредственно в переменных:

let a = 1
let b = false

Массивы и объекты — это ссылочные типы, которые хранятся в памяти отдельно. Область хранения называется кучей, и в начале работы программы она пуста:

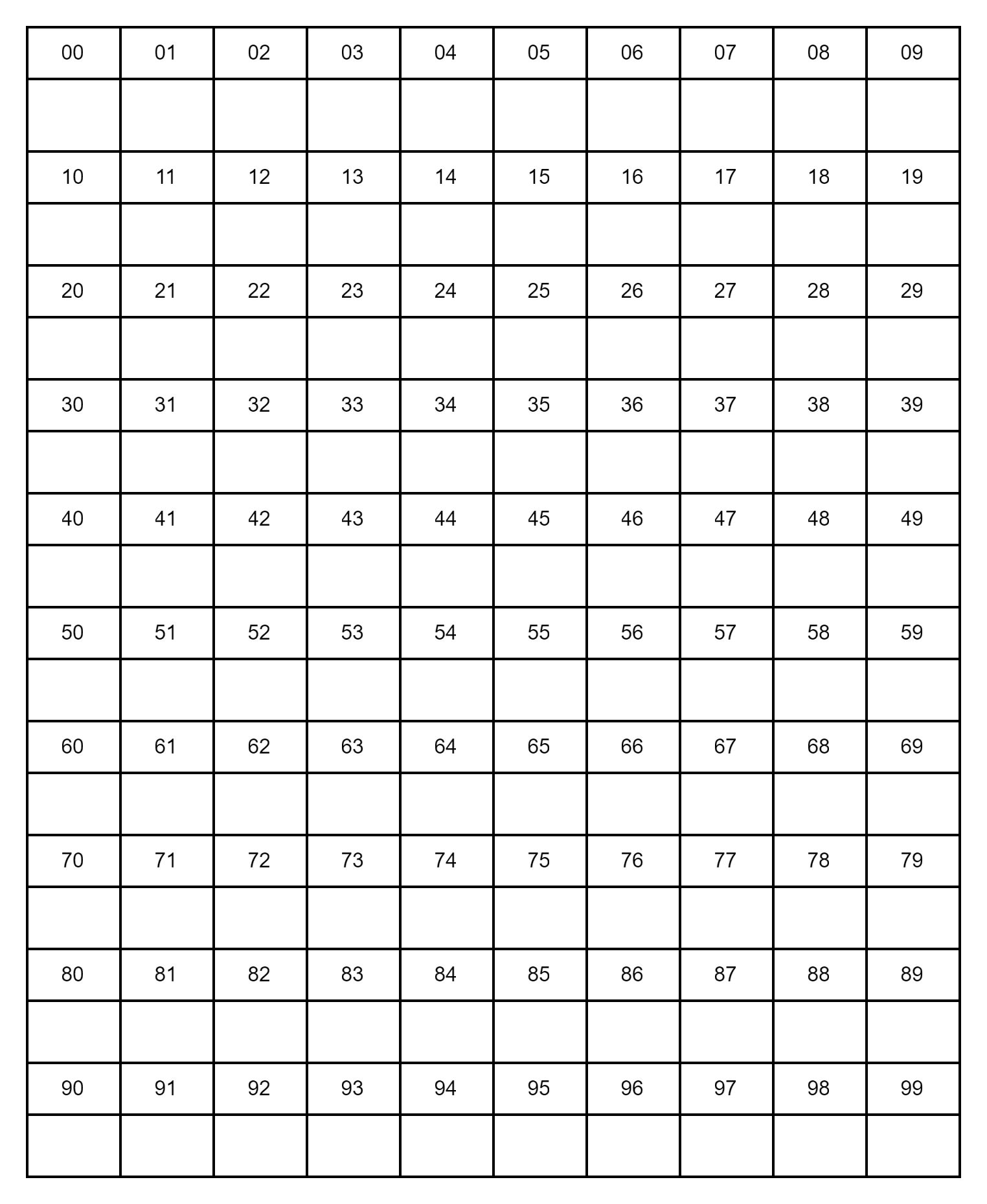
Название «куча» когда-то было сленговым, но прижилось и сейчас используется как официальный термин. Каждая ячейка в куче — это обычная переменная, которая может хранить одно значение. У каждой ячейки есть адрес — ее порядковый номер. Когда мы создаем новый массив, интерпретатор JavaScript размещает его в свободном месте кучи и записывает в переменную адрес массива:

let items = [5, 8, 12, 3]

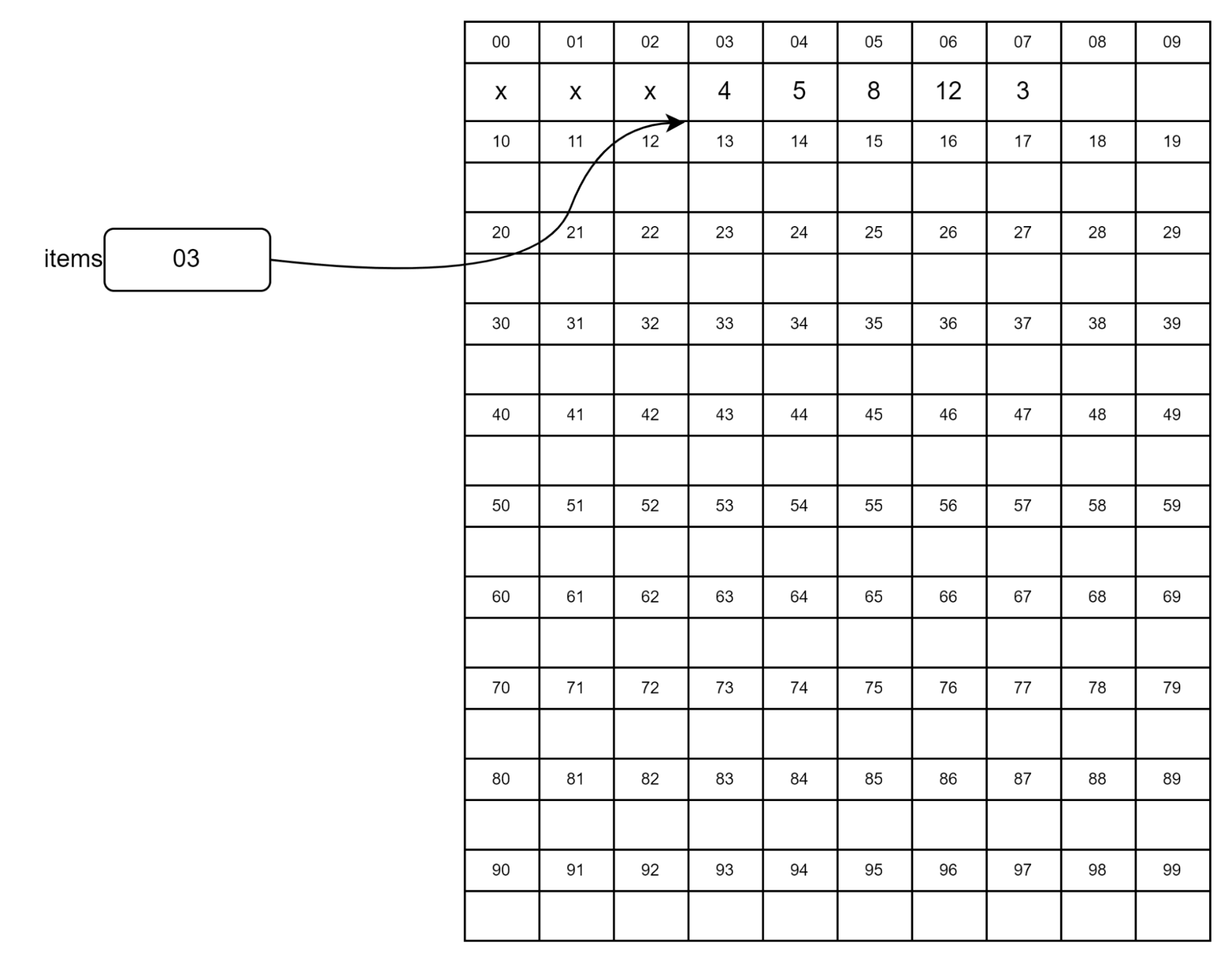
На рисунке вы видите, как хранится массив в памяти. В ячейках с номерами 00, 01 и 02 уже есть какие-то данные — они «заняты», поэтому массив начинается с ячейки 03.

В самой первой ячейке массива хранится его длина или количество элементов, то есть 4. Затем последовательно хранятся сами значения 5, 8, 12 и 3.

Поскольку элементы массива хранятся последовательно, процессор легко определяет адрес элемента по его порядковому номеру в массиве:

console.log(items[2]) // => 12

Массив начинается с адреса 03, где хранится длина массива. Нулевой элемент массива items[0] имеет адрес 04, а второй элемент items[2] — адрес 04 + 2, то есть 06. В этой ячейке находится число 12.

Подобные рассуждения могут запутать, поскольку в ячейках хранятся числа, а адреса ячеек — тоже числа. Если чувствуете, что потеряли нить рассуждений, вернитесь немного назад и повторите.

Порядковый номер элемента в массиве обычно называют индексом — это название пришло из математики.

Определение длины массива и обращение к элементу по индексу — две простые операции, которые мы постоянно используем при работе с массивами. Возьмем для примера функцию, которая вычисляет сумму элементов массива:

const sum = (items) => {
  let result = 0
  for (let i = 0; i < items.length; i++) {
    result = result + items[i]
  }

  return result
}

sum([1, 2, 3, 4]) // 10

Иногда мы хотим расширить массив и добавить к нему несколько элементов. В JavaScript для этого используют метод push():

items.push(7)
items.push(20)

В простом случае, если сразу за массивом есть свободное место, новые элементы попадут туда:

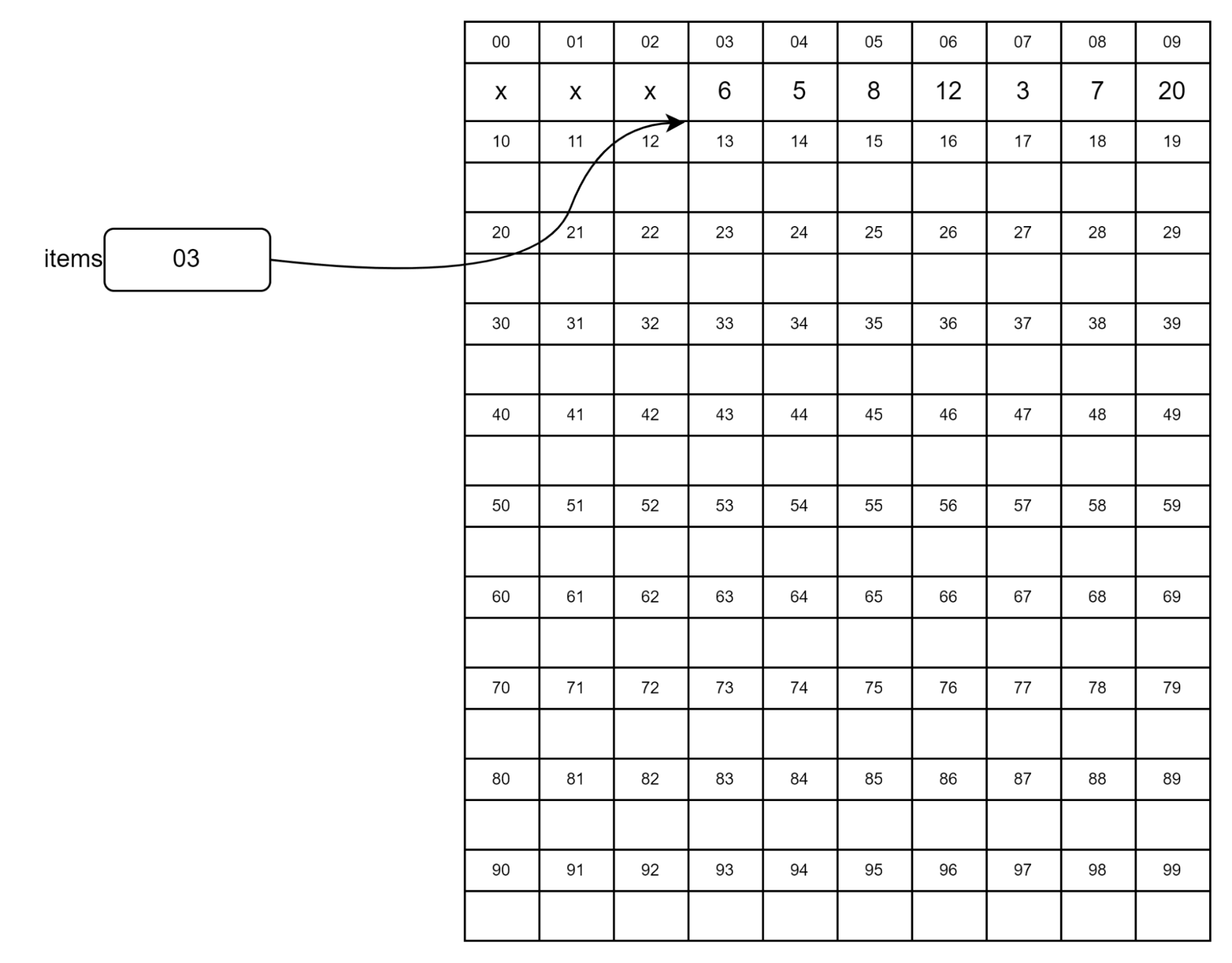
Мы видим, что длина массива теперь равна шести, и в его конце появились числа 7 и 20. А теперь представим, что программист создал после массива еще несколько объектов и свободной памяти сразу за массивом нет:

let items = [5, 8, 12, 3]
let point = { x: -5, y: 7 }
items.push(7)
items.push(20)

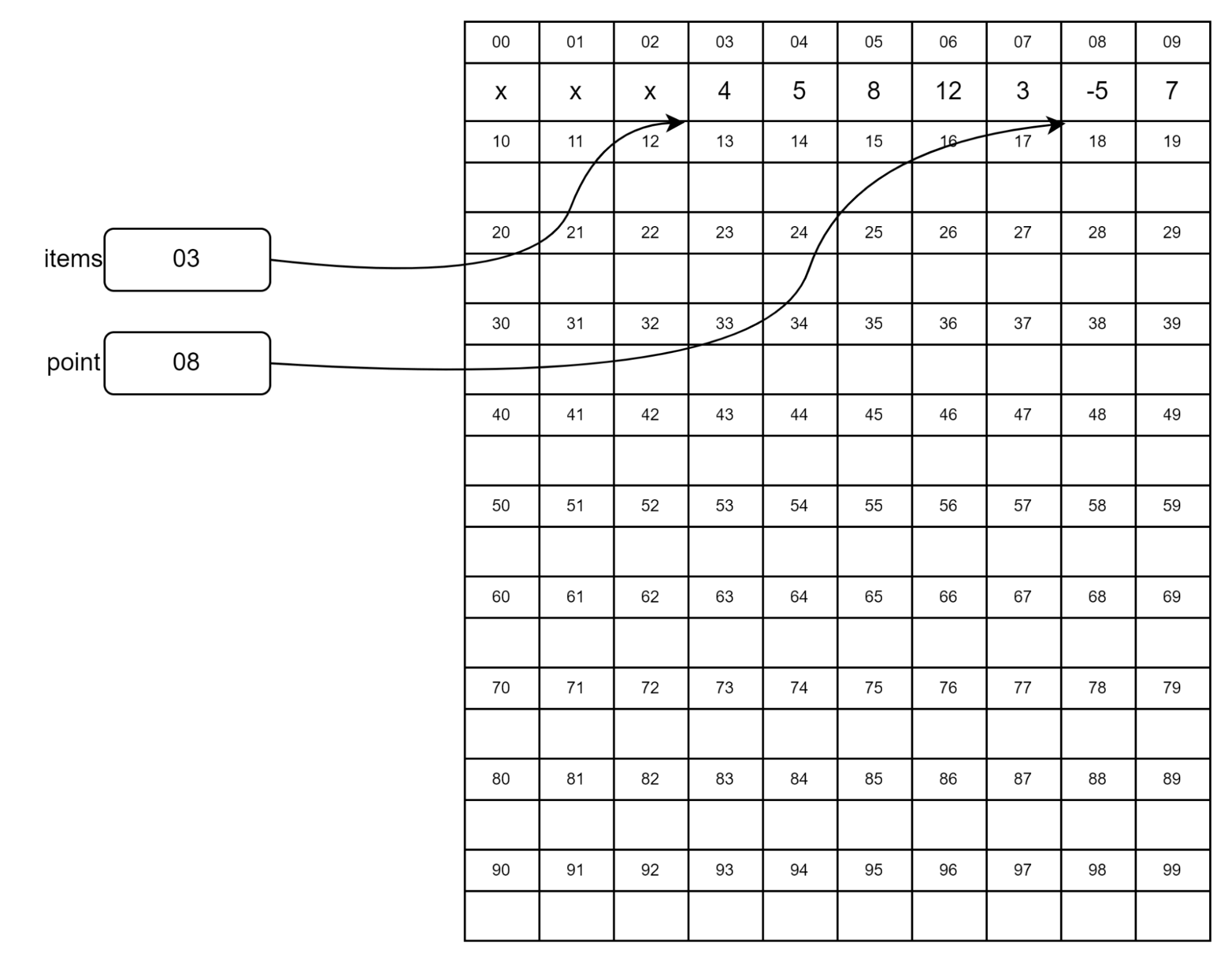
На рисунке сразу за массивом items в куче находится объект point. Кажется, что в этом случае мы не можем расширить массив, ведь элементы должны располагаться в памяти подряд. На самом деле при вызове метода push() интерпретатор копирует весь массив в свободную область памяти и добавляет к ней несколько элементов. Исходная область памяти помечается как свободная:

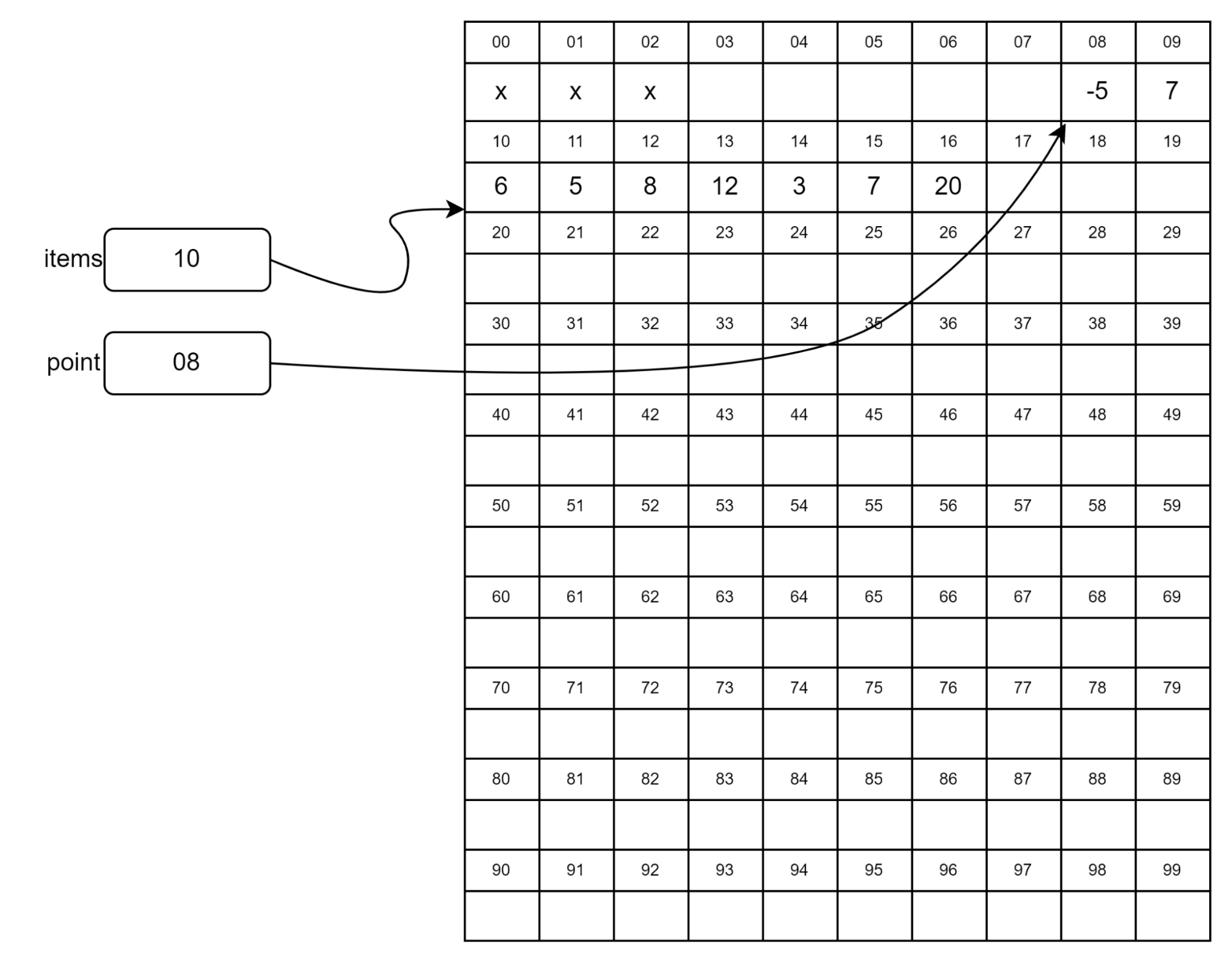
Расширение массива может привести к копированию большого объема данных и замедлению программы. Есть несколько способов борьбы с таким поведением, но копирование все равно случается. Как быть, если нам предстоит часто добавлять и удалять элементы? Можно применить связный список.

Связный список

Это структура, которая решает проблему производительности, если нам приходится часто добавлять и удалять данные. Данные в связном списке хранятся не подряд, а вразброс.

Каждое значение хранится в отдельном объекте, который называется узлом. Помимо значения, объект хранит ссылку на следующий узел списка. В самом последнем узле вместо ссылки на следующий элемент хранится значение null.

Опишем класс, содержащий значение (value) и ссылку на следующий узел (next):

class LinkedListNode {
  constructor(value, next) {
    this.value = value
    this.next = next
  }
}

Список из элементов 5, 8, 12 и 3 может быть создан так:

const head = new LinkedListNode(5,
  new LinkedListNode(8,
    new LinkedListNode(12,
      new LinkedListNode(3, null),
    ),
  ),
)

Оператор new не только создает объект, но и выделяет для него место в памяти. Самый первый элемент односвязного списка часто называют головой (head), поэтому и переменную со ссылкой на голову мы назвали head.

В поле next самого последнего узла находится null — значит, узлов больше нет. В отличие от массива, узлы списка не размещаются в памяти подряд:

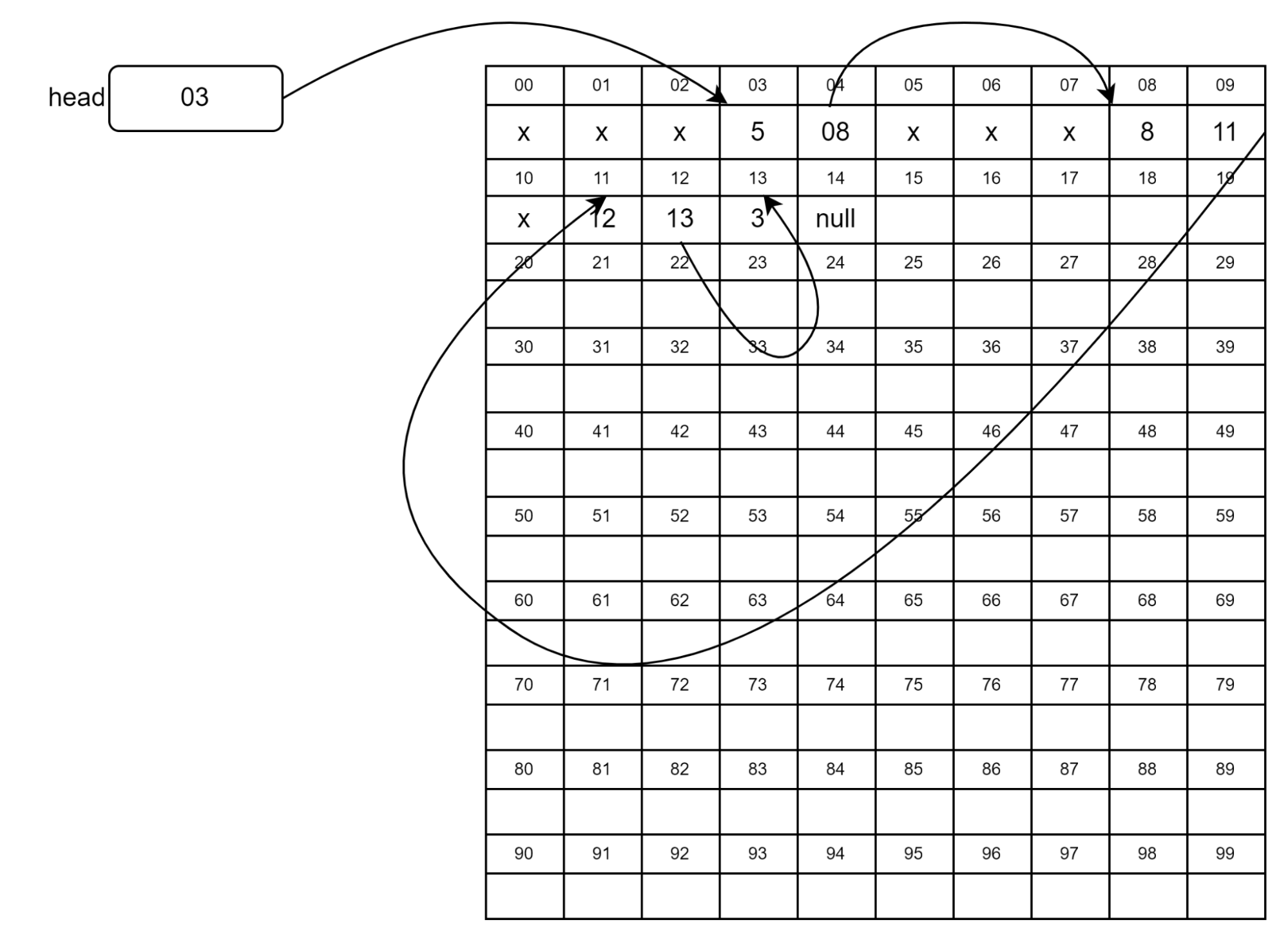
На рисунке узлы списка занимают две ячейки. В первой хранится значение, а во второй — адрес следующего узла или null. Иногда узлы могут располагаться рядом (на рисунке это 12 и 3), но в общем случае это не так.

Вся работа со списком производится через ссылку на его первый элемент, так что переменная head — единственное, что нам нужно для реализации алгоритмов.

Поскольку мы пишем на языке JavaScript, который поддерживает объектно-ориентированное программирование, мы объединим поле head и все наши функции в один класс. Он будет называться LinkedList, что в переводе с английского означает связный список. При создании нового списка в поле head хранится значение null, что означает, что список пустой:

class LinkedList {
  head = null
}

Вставка элемента в начало списка

В простейшем случае, мы вставляем элемент в пустой список. В самом начале значение поля head равно null:

После вставки head указывает на единственный элемент списка:

Мы не рисуем кучу целиком, потому что в реальной программе трудно предугадать, по какому адресу разместится то или иное значение. Конкретные адреса могут сбить с толку.

Поэтому мы просто отмечаем факт, что для нового узла списка в куче были выделены две ячейки, и head указывает на этот узел. Адрес первого узла мы запишем, как addr(1), это позволит нам отличать адреса друг от друга.

После вставки второго узла в начало списка, картина примет такой вид:

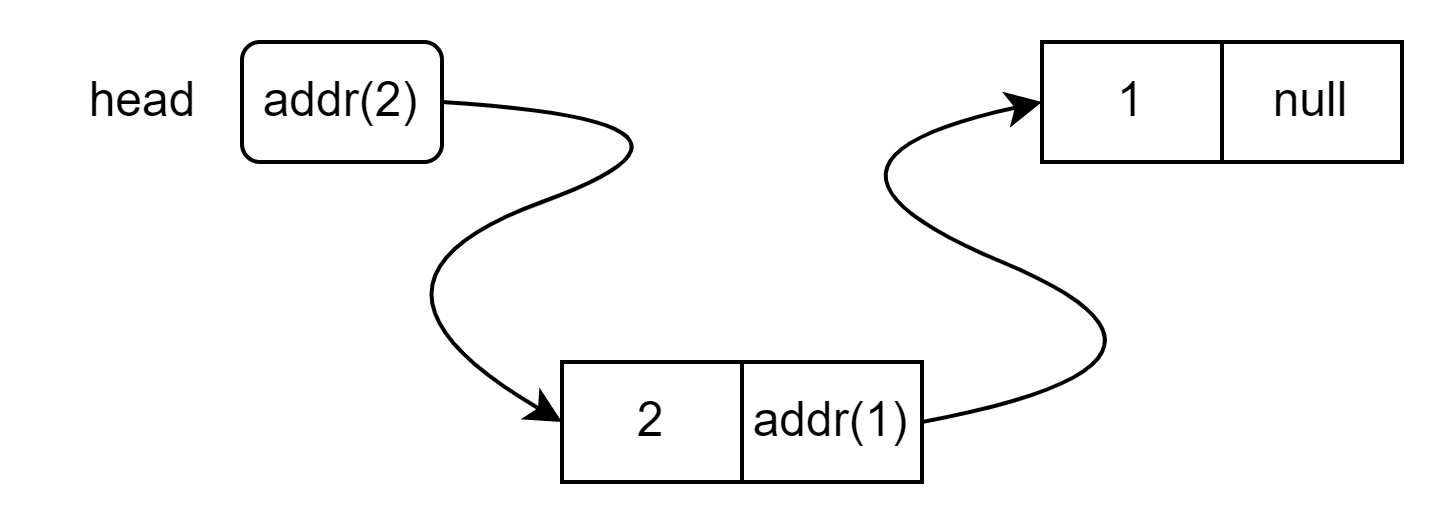
Теперь addr(1), который находился в head, переместился в узел 2, а в head попал адрес второго узла addr(2).

В обоих случаях (вставка в пустой и непустой список), сначала мы создаем узел, куда, в качестве указателя на следующий элемент, записываем текущее значение head.

Взглянем на код:

class LinkedList {
  head = null

  add(value) {
    this.head = new LinkedListNode(value, this.head)
  }
}

Метод add принимает параметр value (значение). Он создает новый узел, помещает туда значение и вставляет узел в начало списка.

Метод состоит из единственной строки:

this.head = new LinkedListNode(value, this.head)

Здесь мы совместили две операции, которые можно было бы записать в две строки:

let node = new LinkedListNode(value, this.head)
this.head = node

Если первый вариант кода кажется вам сложным, вы можете остановиться на втором. Обычно программисты, по мере чтения кода, привыкают к часто встречающимся конструкциям. Знакомые конструкции уже не кажутся сложными.

Насколько быстро работает метод add? Создание объекта может занимать большое время, но у нас простой конструктор с двумя присваиваниями, поэтому работать он будет быстро.

Время добавления узла в начало всегда одно и то же и не зависит от размера списка, поэтому в данном случае речь идет об алгоритмической сложности O(1).

Вставка элемента в середину или конец списка

Вставка в середину или конец — сложная операция. В отличие от массива, мы не можем сразу получить второй или пятый узел списка. Мы должны перебрать все узлы с начала, чтобы понять, куда вставить новое значение:

insert(index, value) {
  if (this.head === null) {
    this.head = new LinkedListNode(value, null);
  } else if (index === 0) {
    this.add(value);
  } else {
    let current = this.head;
    while (current.next !== null && index > 1) {
      current = current.next;
      index = index - 1;
    }

    current.next = new LinkedListNode(value, current.next);
  }
}

Вызов insert(index, value) означает, что узел со значением value будет вставлен в середину списка в позицию index. Если index равен 0, то значение вставится перед первым элементом — так же, как при вызове add:

if (index === 0) {
  add(value)
}

Если список пустой, index не может быть больше нуля, потому что мы можем вставить значение только в начало списка. Как должна поступать в этом случае функция решает ее автор. Мы можем генерировать ошибку или попытаться выполнить какое-то разумное действие.

Пойдем вторым путем — если список пустой, при больших значениях index будем вставлять элемент в самое начало:

if (this.head === null) {
  this.head = new LinkedListNode(value, null)
}

А в случае, если index оказывается за концом списка, будем вставлять элемент в самый конец. Для этого будем проверять два условия: либо мы нашли элемент с номером index, и он не в конце, либо мы достигли последнего элемента:

while (current.next !== null && index > 1) {
  current = current.next
  index = index - 1
}

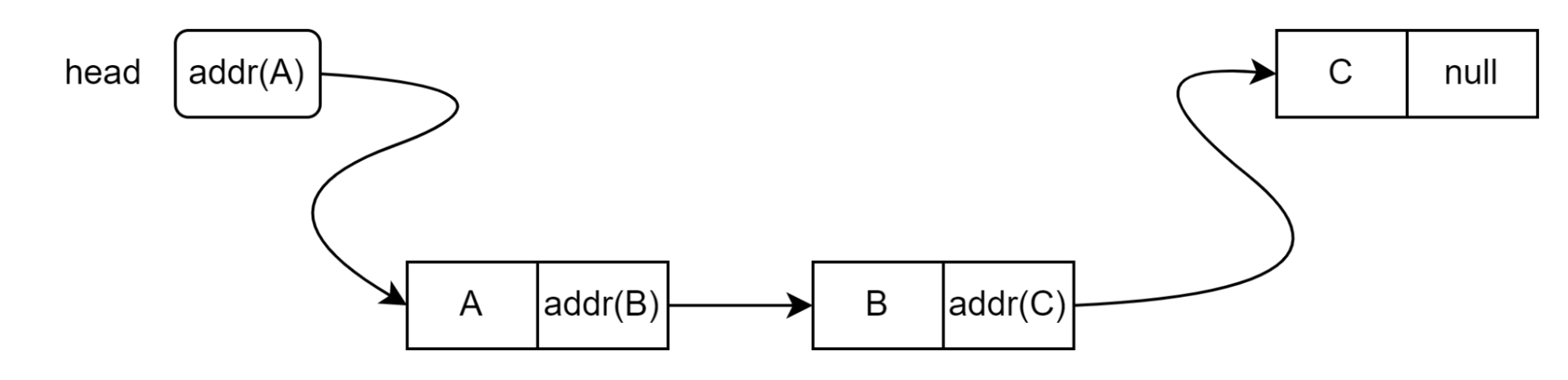
Нарисуем, что должно происходить при вставке. Пусть в начале у нас есть список из элементов A и C. Мы хотим вставить элемент B после A, но перед C:

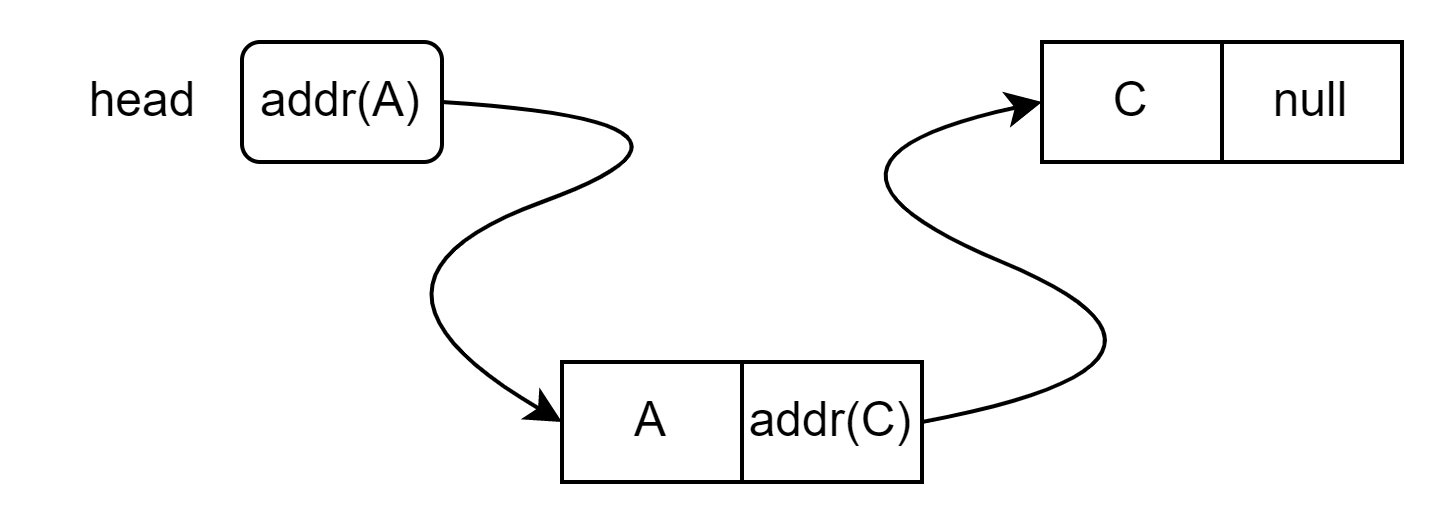
Когда цикл заканчивается, переменная current указывается на узел A:

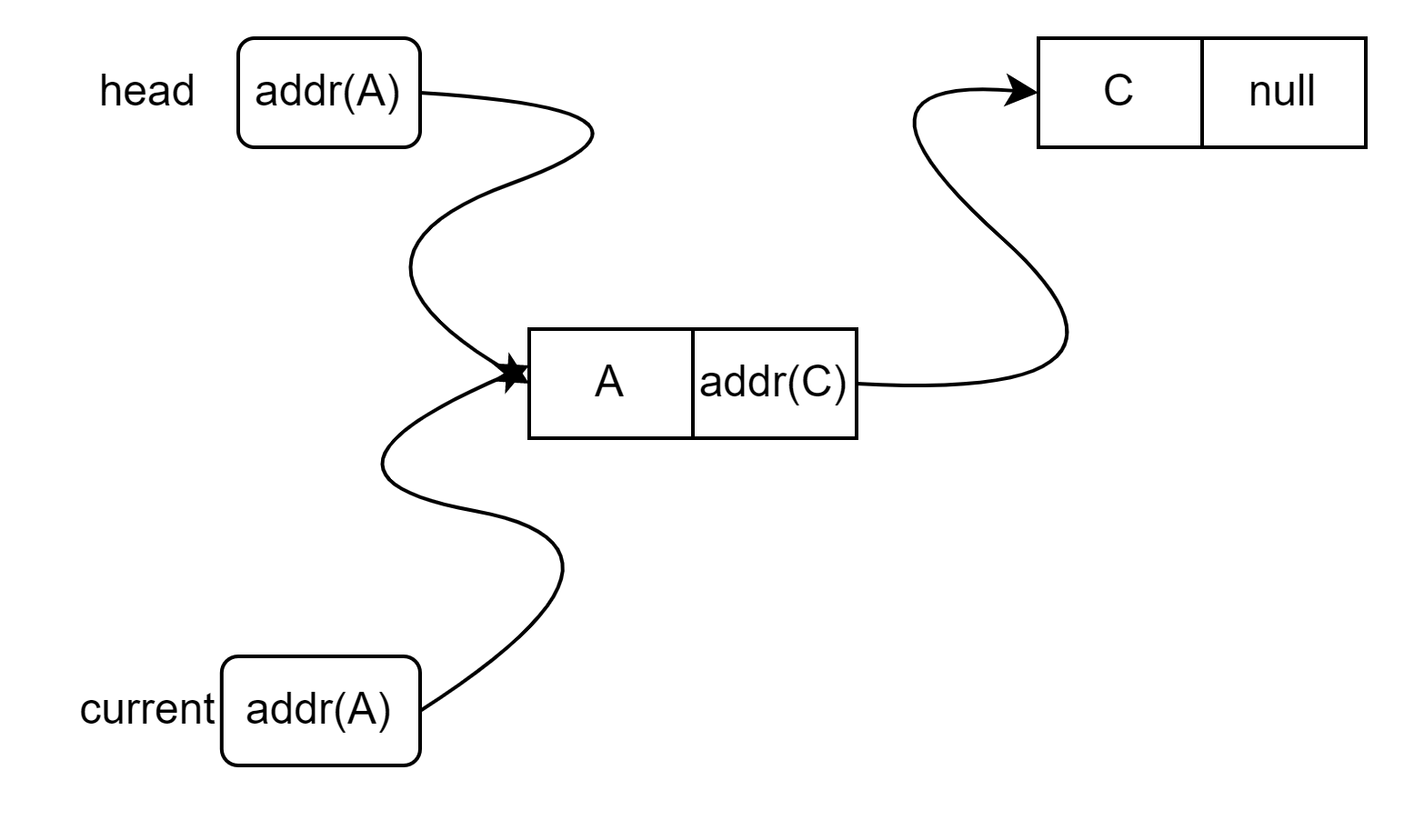
После вставки мы получим такую картину:

Перед вставкой в current.next хранится ссылка на C, но теперь она должна переехать в узел B, а в current.next мы запишем ссылку на новый узел B:

current.next = new LinkedListNode(value, current.next)

Поиск элемента

При работе с массивом важное значение имеет индекс элементов. При работе со списком индекс практически не используется, хотя формально мы можем найти третий или семнадцатый узел списка.

Если при поиске элемента в массиве, функции часто возвращают индекс элемента, то для списка — логическое значение true или false.

Вместо ответа на вопрос «если такой элемент в массиве есть, где он находится», функция поиска в списке отвечает на вопрос «есть ли такой элемент в списке»:

contains(value) {
  let current = this.head;
  while (current !== null) {
    if (current.value === value) {
      return true;
    }

    current = current.next;
  }

  return false;
}

Здесь у нас простой цикл. Мы пробегаем по всем узлам, пока не натыкаемся на null. Если мы встретили null и не нашли значения, значит, в списке его нет — в конце цикла мы возвращаем false.

Если значение находится в одном из узлов, мы прерываем цикл и сразу возвращаем true:

if (current.value === value) {
  return true
}

В конце цикла важно переходить к следующему узлу, иначе цикл станет бесконечным:

current = current.next

Определение длины списка

В отличие от массива, длина списка нам неизвестна, ее нужно вычислить. Мы заводим счетчик и пробегаем по всем узлам списка, увеличивая его на каждой итерации. Длина пустого списка считается равной нулю.

В целом, код получается простой:

length() {
  let result = 0;
  let current = this.head;

  while (current !== null) {
    result = result + 1;
    current = current.next;
  }

  return result;
}

Переменная result — это наш счетчик. Переменная current на каждой итерации указывает на текущий узел списка. Когда она становится равной null, список пройден до конца. Перейдя к следующему узлу, мы увеличиваем счетчик, поэтому в конце цикла его значение равно количеству узлов.

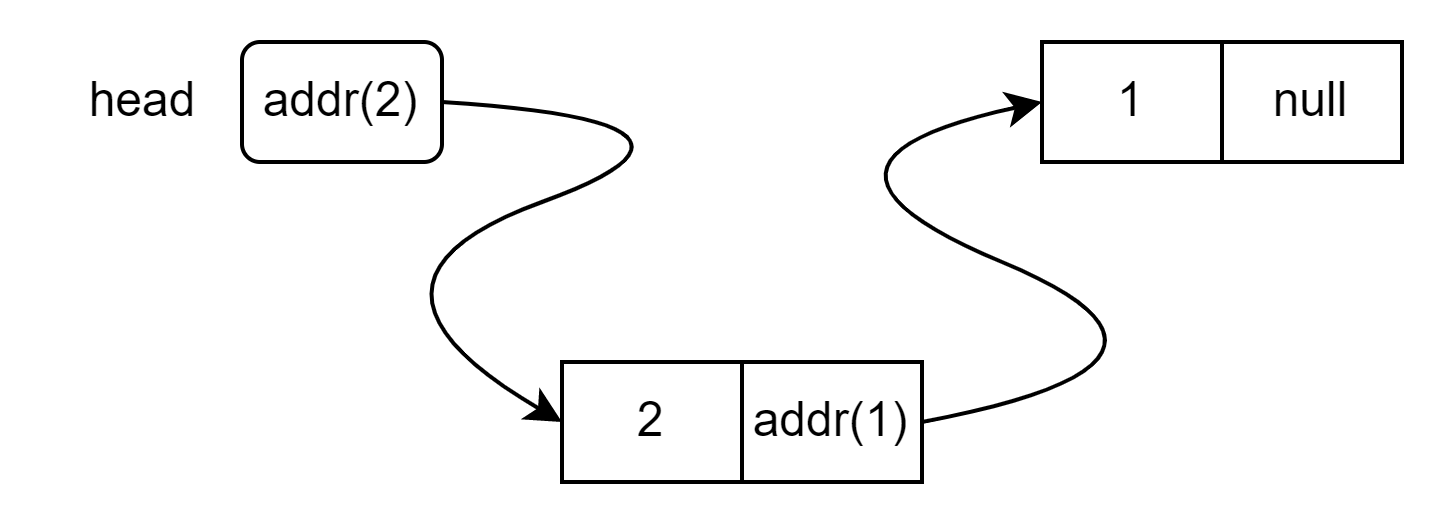
Удаление элемента из начала списка

Удаление элемента из начала списка такое же простое, как и вставка. Мы будем возвращать значение из удаленного узла в качестве результата.

Если список пустой, мы не будем ничего удалять, и в качестве результата вернем undefined:

remove() {
  if (this.head === null) {
    return undefined;
  }

  const value = this.head.value;
  this.head = this.head.next;

  return value;
}

При удалении в this.head попадает ссылка на следующий узел из первого узла. Когда в списке остается один узел, там находится null. После удаления последнего узла this.head становится равным null, что для нас означает пустой список.

Нам не приходится как-то по-особому описывать этот случай в коде — наш код работает для списков любой длины.

Рисунки помогут разобраться, как удаляются узлы из списка:

Удаление элемента из середины или конца списка

Теперь, когда мы умеем вставлять элементы в начало и середину списка, и удалять их из начала списка, удаление узлов из середины не должно представлять для нас проблемы.

Мы просто скомбинируем написанный нами ранее код:

removeAt(index) {
  if (this.head === null) {
    return undefined;
  } else if (index === 0 || this.head.next === null) {
    return this.remove();
  } else {
    let current = this.head;
    while (current.next.next !== null && index > 1) {
      current = current.next;
      index = index - 1;
    }

    const value = current.next.value;
    current.next = current.next.next;

    return value;
  }
}

Единственное нововведение по сравнению с предыдущим кодом заключается в том, что при удалении узла из середины, нам нужно просматривать список на два элемента вперед. Если мы хотим удалить последний узел в списке, нам придется вносить изменения в предпоследний — менять там значение ссылки next.

Поэтому нам приходится, как особый случай, обрабатывать список из одного элемента. Впрочем, эту проверку мы можем совместить с проверкой на удаление из начала:

if (index === 0 || this.head.next === null) {
  return remove()
}

Меняется и условие в цикле. Если раньше мы проверяли, что current.next не равен null, то теперь мы проверяем current.next.next. Иными словами, вместо ответа на вопрос «есть ли следующий узел в списке», мы отвечаем на вопрос «есть ли узел за следующим узлом».

В остальном код остается прежним.

Сравнение массива и связного списка

Осталось разобраться, в каких случаях использовать массив, а в каких связный список. Об этом нам расскажет таблица, где мы сравним производительность операций:

Поиск и в массиве и в списке не очень быстрый, всего O(n).

Образно, массив похож на ежедневник, а связный список — на дневник. В ежедневнике нам важно быстро найти дату, а в дневнике — следующую пустую страницу. Если мы захотим найти все записи на заданную тему, нам придется перечитывать что дневник, что ежедневник.

Выводы

В этом уроке мы изучили односвязный список. Повторим важные тезисы из урока:

• Структура данных — это способ хранения данных в памяти компьютера. Одни и те же операции могут быть быстрыми для одних структур и медленными для других
• Сложные структуры данных — объекты и массивы — хранятся в куче.
• Массив не очень хорош, если нам приходится добавлять или удалять элементы. Связный список хорош, если необходимо добавлять новые данные в начало
• Определение длины и поиск элемента по индексу быстрее в массиве. Массив и связный список похожи на ежедневник и дневник