Сначала графы использовались только в математике — с их помощью решались задачи, связанные с картами. Со временем графы пришли и в программирование, потому что они подходят для решения широкого круга задач:
-
Составление расписаний
-
Заполнение грузовых контейнеров
-
Работа с компьютерной графикой
-
Поиск дешевых авиабилетов
-
Построение маршрутов на реальных картах и в компьютерных играх
Все эти непохожие задачи решаются одним и тем же способом — с помощью алгоритмов на графах.
В этом курсе мы изучим с самыми важными алгоритмами на графах, а пока познакомимся с самым главным термином этого курса.
Что такое графы
Графы — это важное, но случайное изобретение. Математик Леонард Эйлер придумал их, когда решал задачу о кенигсбергских мостах.
По условию этой задачи в городе Кенигсберге было семь мостов. Его жители пытались составить маршрут, который позволил бы обойти все мосты, не проходя ни по одному мосту дважды. Схематически карта города выглядит так:
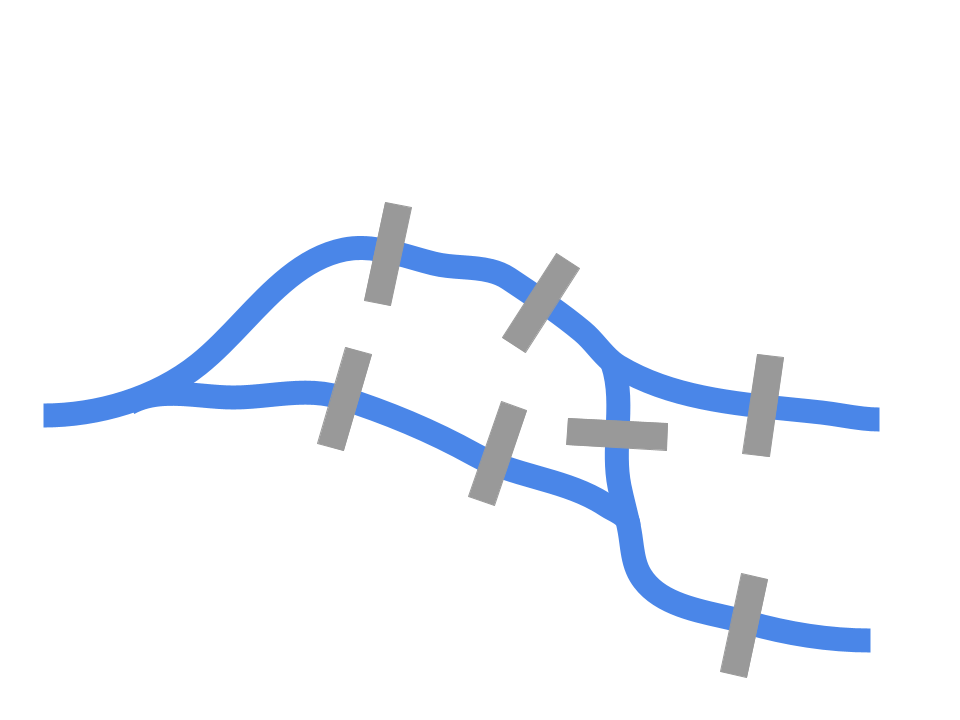
Эйлер поставил на карте четыре точки и соединил их дугами:
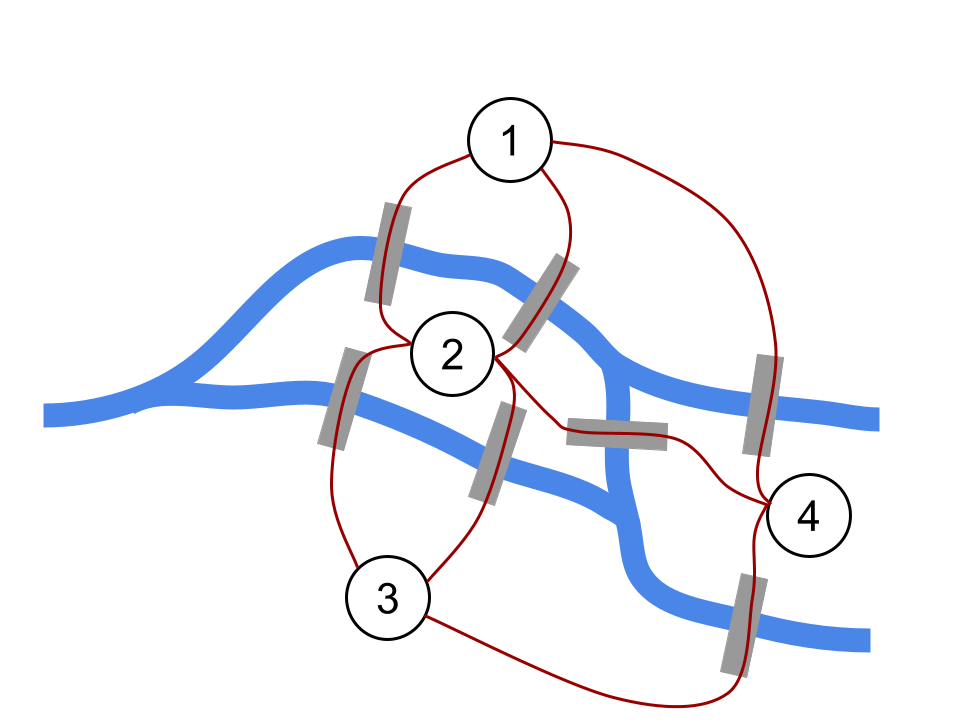
Карту города можно убрать совсем и увидеть рисунок, с которым работал Эйлер:
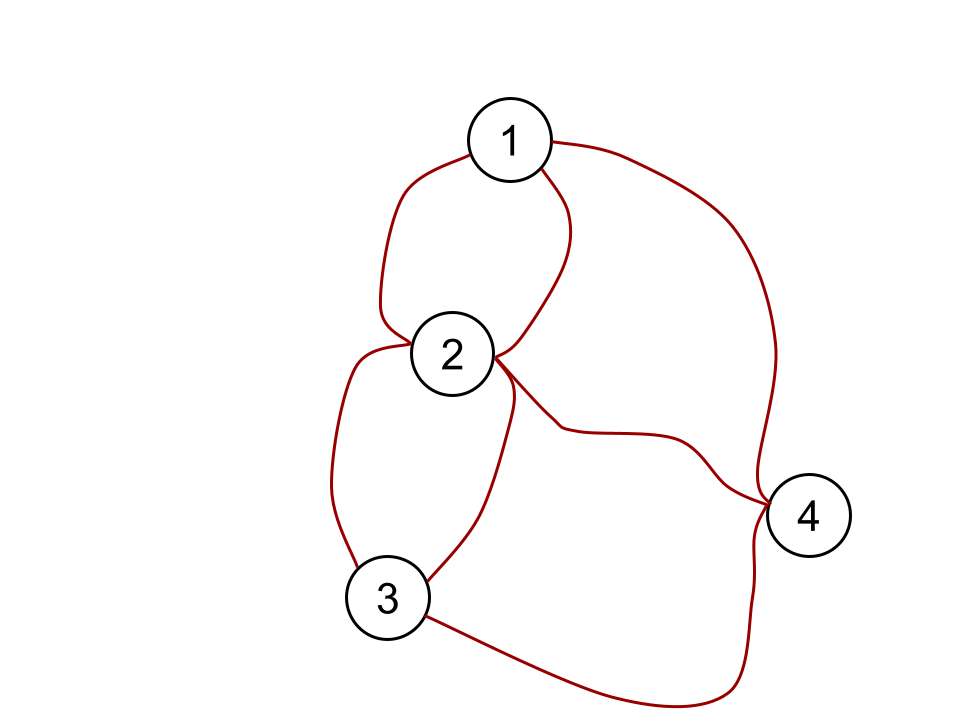
Значительно упростив представление задачи, Эйлер доказал, что нужного маршрута не существует. Более того, он вывел общее правило, которое помогает определить, можно ли построить подобный маршрут на произвольной карте.
Так Эйлер изобрел метод, который позволяет сводить сложные задачи к наглядным рисункам. Фигуры, подобные рисунку Эйлера, стали называть графами. Точки называются вершинами графа, а соединяющие их дуги — ребрами.
Название «граф» происходит от греческого слова графо — «писать» или «рисовать». Слова «картография» и «фотография» произошли из этого же корня.
Разглядывая рисунок, Эйлер понял такую закономерность:
-
Если из вершины выходит четное количество ребер, то ее можно «пройти», побывав на каждом ребре ровно один раз
-
Если же ребер нечетное число, то между собой можно связать только две нечетных вершины
На графе эта закономерность выглядит так:
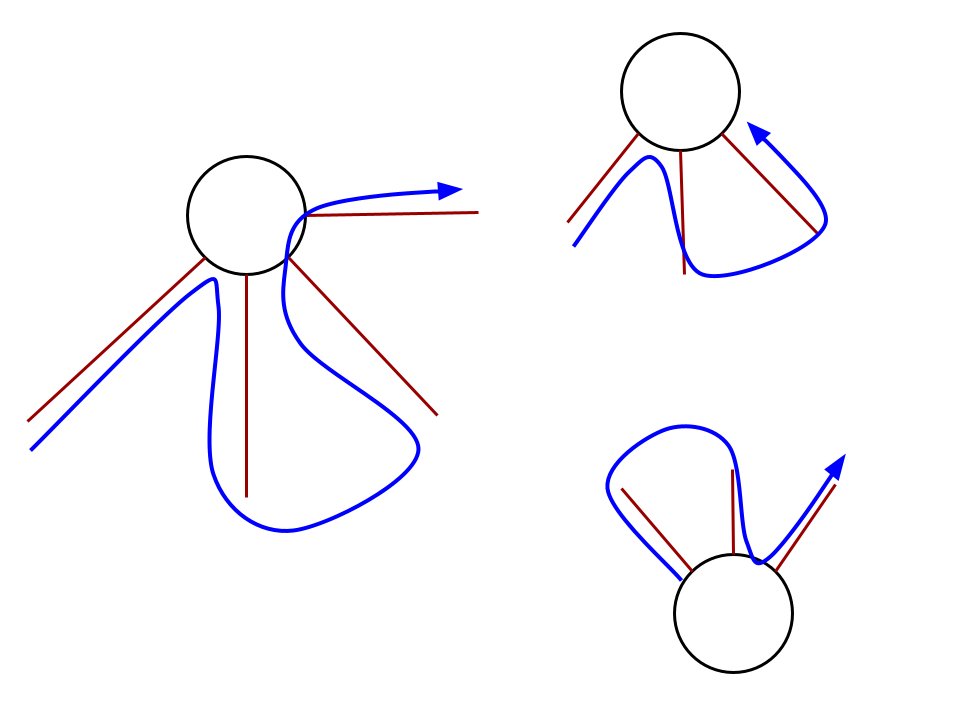
Так Эйлер сформулировал правило:
Можно посетить все вершины графа, пройдя по каждому ребру ровно один раз, но только в том случае, если у графа только две нечетные вершины или вообще нет нечетных вершин
По этому правилу получается, что кенигсбергские мосты обойти нельзя, потому что они образуют граф с четырьмя нечетными вершинами. Эйлер не просто решил конкретную головоломку, но и сформулировал общую теорему, которую можно приложить к самым разным задачам.
Другие задачи на графах
Одна из распространенных задач с графами — это выдача купюр.
Обычно банкоматы стараются выдать сумму наименьшим числом банкнот. Если вы попросили 5000 рублей, банкомат выдаст 5000 рублей одной купюрой. Если такой купюры нет, то банкомат выдаст 2000, 2000 и 1000 рублей. Существует быстрый алгоритм, который всегда оптимально решает эту задачу.
То же самое работает и в логистике. Например, при перевозке контейнеров их заполняют ящиками стандартных размеров. Ящики нужно разместить как можно плотнее, чтобы обойтись минимальным числом контейнеров. Графы позволяют решить и эту задачу.
Еще один пример — текстовые редакторы. Они не только опознают слова с ошибками, но и предлагают варианты замены. Очень непросто найти в словаре несколько слов, похожих на ошибочное, но графы могут разобраться и с этим.
В целом, задачи на графах встречаются в самых разных областях. Но есть одна проблема — их не всегда легко опознать.
Поэтому в этом курсе мы затронем задачи, которые на первый взгляд вообще не имеют отношения к графам.
Например, к таким задачам относятся:
-
Задача коммивояжера
-
Задача о рюкзаке
Они заметно отличаются по формулировке, но при этом решаются с помощью одних и тех же алгоритмов.
Точность и производительность
Кстати, графы — та область программирования, где часто применяются приближенные решения вместо точных. Иногда эти алгоритмы с приближенными решениями называются эвристическими.
Дело в том, что точные алгоритмы на графах работают настолько медленно, что их нельзя применять на практике даже для очень небольших наборов данных.
В теории алгоритмов есть классы сложности, с которым мы познакомимся в конце курса.
Мы узнаем, что такое задачи класса NP и почему они считаются сложным. Также мы познакомимся с несколькими приближенными алгоритмами и решим с их помощью несколько разных задач.
Выводы
Повторим ключевые выводы курса:
-
Задачи на графах часто решаются графически — в таких случаях очевидно, что задачу надо решать через графы
-
Иногда с первого взгляда не понятно, что задача решается с помощью графов. В этом курсе мы научимся распознавать такие задачи
-
Точные алгоритмы на графах работают очень медленно
-
Чтобы быстро решать задачи на графах, программисты прибегают к эвристическим алгоритмам
-
В курсе мы разберем несколько эвристических алгоритмов
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
