Теория: Дополнение

Прежде чем мы определим, что такое дополнение множества, вспомним определения универсального множества и подмножества — эти термины будут часто использоваться в этом уроке. Универсальное множество — это множество всех элементов, которые рассматриваются в конкретной задаче или ситуации.

Допустим, нам нужно найти все целые числа, которые удовлетворяют неравенству -3 < x < 2. Нам дано универсальное множество целых чисел:

{..., -3, -2, -1, 0, 1, 2, 3, ...}

Целые числа, которые удовлетворяют неравенству:

{-2, -1, 0, 1} — это подмножество универсального множества

Допустим, у нас есть множество A — подмножество некоторого универсального множества U. Дополнение A — это все остальные элементы из U, которые не вошли в A.

В нашем примере выше, дополнение для {-2, -1, 0, 1} — это множество, содержащее все целые числа, которые не удовлетворяют неравенству: {..., -3, 2, 3, ...}.

Мы можем проиллюстрировать это определение на другом примере. Если нашим универсальным множеством являются города России, то возможным подмножеством является множество городов миллионников: A={Москва, Санкт-Петербург, Новосибирск, Екатеринбург, Казань, Нижний Новгород, Челябинск, Самара, Уфа, Ростов-на-Дону, Омск, Волгоград, Воронеж, Краснодар, Красноярск, Пермь}.

Тогда дополнением A будет множество, содержащее все остальные города, которые не являются миллионниками.

Существуют различные способы обозначения дополнения множества с помощью нотации. Например, можно использовать знак простого числа. Иногда используется надстрочная строчная буква c. Над именем исходного множества может стоять черточка или символ подчеркивания. Мы будем использовать '.

В этом уроке мы подробно рассмотрим дополнение множества, его определение и свойства.

Что такое дополнение множества?

Простыми словами, дополнение множества A — это разность между универсальным множеством и множеством A.

Это тождество можно записать так:

A' = {x  ∈  U : x  ∉  A}

В дополнение входят те элементы x из множества U, которые не входят в A.

Условные обозначения

Дополнение любого множества представляется как A', B', C' и т.д. Другими словами, если задано универсальное множество (U) и подмножество универсального множества (A), то разность универсального множества (U) и подмножества универсального множества (A) является дополнением подмножества, то есть A' = U - A.

Рассмотрим на таком примере:

• Дано U, в которое входят все простые числа до 25
• Множество A = {2, 3, 5}

Найдем дополнение:

• Шаг 1: Проверка универсального множества и множества, для которого нужно найти дополнение: U = {2, 3, 5, 7, 11, 13, 17, 19, 23}, A = {2, 3, 5}
• Шаг 2: Вычитание: (U - A)
• Шаг 3: Здесь U - A = A'
  • = {2, 3, 5, 7, 11, 13, 17, 19, 23} - {2, 3, 5}
  • = {7, 11, 13, 17, 19, 23}

Диаграмма

Для лучшего понимания посмотрите на приведенную ниже диаграмму Венна, которая ясно показывает дополнение множества A, то есть A':

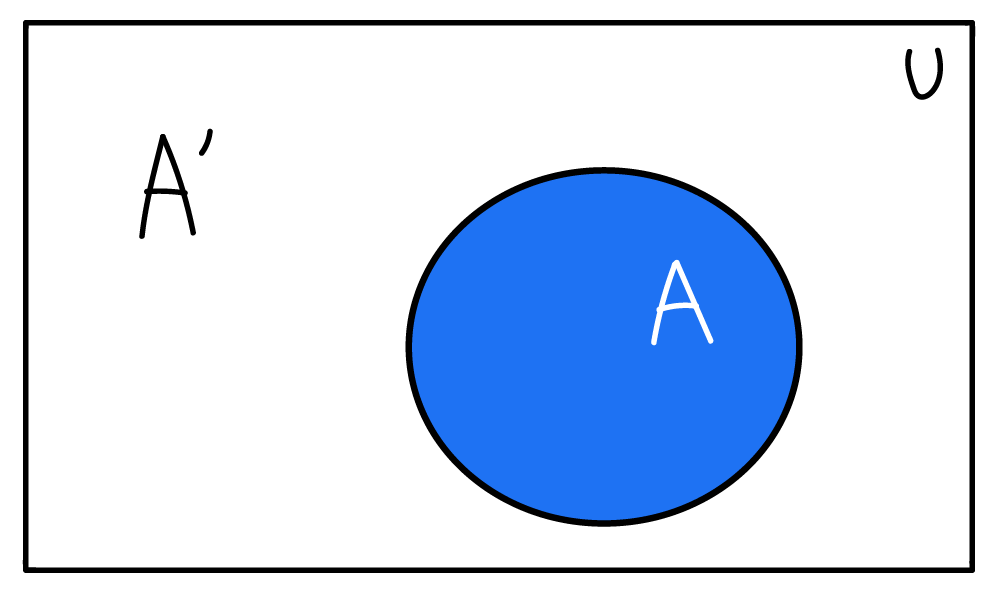
Здесь A' не является частью множества A, и множество A также не является частью A'. A и A' являются подмножествами U.

Свойства дополнения множества

Ниже перечислены свойства дополнения множества, которые включают в себя:

• Законы дополнения
• Закон двойного дополнения
• Закон пустого множества
• Закон универсального множества

Законы дополнения

• Если A является подмножеством универсального множества, то A' также является подмножеством универсального множества. Поэтому объединение A и A' является универсальным множеством, представленным как A ∪ A' = U
• Пересечение множеств A и A' дает пустое множество "∅", представленное как A ∩ A' = ∅

Рассмотрим на таком примере:

• Если U = {1 , 2 , 3 , 4 , 5 } и A = {4 , 5} и B = {1, 2}
• A' = {1 , 2 , 3 } и B' = {3, 4, 5}
• A ∪ A' = U = { 1 , 2 , 3 , 4 , 5}
• Кроме того, A ∩ A' = ∅

Закон двойного дополнения

• Дополнением дополненного множества является исходное множество (A')' = A
• Дополнение множества A', где само A' является дополнением A, двойное дополнение A, таким образом, является самим A

В предыдущем примере U = {1 , 2 , 3 , 4 , 5} и A = {4 , 5}, тогда A' = {1 , 2 , 3 }. Дополнение A' = (A')' = {4, 5}, что равно множеству A.

Закон для пустого множества и универсального множества

• Дополнением универсального множества является пустое множество или нулевое множество (∅), а дополнением пустого множества — универсальное множество
• Поскольку универсальное множество содержит все элементы, а пустое множество не содержит никаких элементов, следовательно, их дополнения прямо противоположны друг другу, что представляется как ∅' = U И U' = ∅

В примере выше, множество U = {1, 2, 3, 4, 5} содержит все элементы множества A, а множество B как универсальное множество содержит все элементы, поэтому U' = ∅ (пустое множество) и ∅' = {1, 2, 3, 4, 5}.

Выводы

• Дополнением универсального множества является пустое множество или нулевое множество
• Множество пересечения содержит элементы, которые являются общими для обоих множеств
• Объединение двух множеств — это множество, содержащее все элементы, которые находятся в A или B или в обоих