До текущего момента мы работали только со списками. Но как мы помним свойство замыкания множества относительно операции позволяет строить из пар иерархические структуры, т.е. те структуры, части которых сами являются составными структурами. Самый яркий представитель иерархических структур - это деревья.
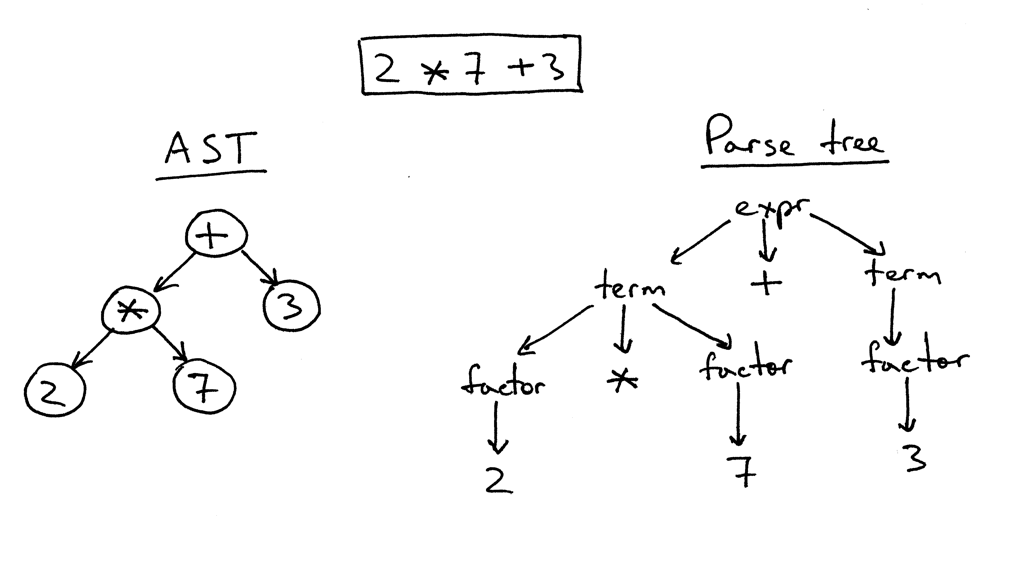
Деревья бывают очень разные. Вообще это название произошло от обычных деревьев, потому что на него можно смотреть, как на иерархическую структуру. На стволе расположены ветки, на ветках могут быть тоже ветки, на которых, в свою очередь, есть ещё ветки, на которых есть листья. Деревьев существует очень много видов как в реальной жизни, так и в программировании, в Computer Science их много десятков, если не сотен.
При этом все они обладают общими свойствами и имеют соответствующий словарь терминов. Давайте с ними познакомимся. Деревья в программировании так или иначе встречаются всем, любым программистам, на любом языке, в любой области.
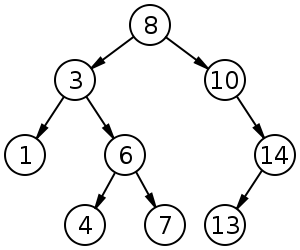
- Узел — это любой элемент дерева. Иногда говорят вершина, нода.
- Корневой узел — самый верхний узел дерева (на картинке это узел под номером 8).
- Лист — это узел, не имеющий дочерних элементов. Листья расположены в самой глубине дерева.
Особенности
- Рекурсивное определение
- Естественный способ обработки - рекурсия
Какие особенности присущи таким структурам?
Определение дерева является рекурсивным. Потому что постепенно идёт рекурсивный спуск в глубину, и любой элемент может оказаться тоже деревом или поддеревом, которые в свою очередь тоже могут содержать деревья или поддеревья. Как можно догадаться, естественный способ обработки таких элементов — это рекурсия.
Вот пример с использованием языка Haskell, в котором дерево можно определить как тип данных, используя по сути математическое определение.
data Tree a = EmptyTree | Node a (Tree a) (Tree a)
Дерево - это либо пустое дерево (EmptyTree), либо нода, которая содержит в себе элемент (Node a), который содержит два поддерева (Tree a).
Это определение бинарного дерева, но общий принцип понятен. Фактически одна такая строчка определяет бинарное дерево любой сложности, т.е. все они будут подходить под это определение.
<html>
<body>
<h1>Сообщество</h1>
<p>Общение между пользователями Хекслета</p>
<div class='hexlet-community'>
<div class='text-xs-center'>
<div class='fa fa-spinner'></div>
</div>
</div>
</body>
</html>
Давайте вернемся к нашему HTML. В одном из первых уроков мы сказали, что на самом деле это древовидная структура, хотя мы работали с ним как со списком. Корнем является тег html. При этом вкладывать можно не всё во всё, есть определённые правила, по которым это делается. Но в любом случае это древовидная структура, которая позволяет нам строить иерархию любой глубины, что обычно и происходит. Поэтому в общем случае с HTML и работают как с деревом, а не просто списком.
Вспомним, что с помощью пар можно представлять деревья совершенно по-разному. В общем-то, благодаря замыканию мы можем построить любые типы деревьев.
Давайте посмотрим конкретную задачу, решаемую в контексте работы с деревьями. Фактически мы расширим ту функциональность, которую использовали для работы со списками. Для того, чтобы построить дерево, нам достаточно тех же самых списков, а в общем случае — пар.
Количество листьев
import { head, tail, l } from 'hexlet-pairs-data';
const tree = l(l(1, 2), l(3, l(4, 5)), 6);
const countElements = (tree) => {
if (!isList(tree)) {
return 1;
}
if (isEmpty(tree)) {
return 0;
}
return countElements(head(tree)) + countElements(tail(tree));
};
countElements(tree); // 6
В примере выше мы создаём дерево, по факту просто используя списки внутри списков, что достаточно очевидно. Можно представить, как дерево визуально будет выглядеть. У нас есть список, в котором есть вложенный список, дальше ещё один список, вложенный в другой список и какой-то элемент, т.е. листья есть на разных уровнях нашего дерева. Давайте попробуем подсчитать количество элементов. Здесь используется обычный рекурсивный процесс, в котором в конечном итоге происходит следующее.
Мы получаем head(tree) и tail(tree), "голову" и "хвост" списка. При этом в отличие от работы со списками в предыдущих уроках, "голова" тоже может оказаться поддеревом, поэтому функцию countElements мы рекурсивно применяем и к "голове" и к "хвосту". Нам нет разницы, работаем мы с левой или с правой частью, ведь расшириться вглубь может любая из них.
Данный вид рекурсии называется уже не линейной, а древовидной, так как каждый countElements внутри вызывает две функции countElements, что её раздваивает. Если посмотреть все вызовы этой функции, можно увидеть, что они "расползаются" по дереву.
В примере выше есть две проверки. Если это не список, т.е. мы дошли до листового узла, мы возвращаем единицу. Если список пустой, т.е. мы обработали весь текущий уровень, то возвращаем 0. И в конце данная функция возвращает количество листьев в дереве.
Обход в глубину
Рассмотрим еще один пример, в котором не требуется накапливать результат. Предположим, что у нас есть список списков любой вложенности, который содержит числа. Все что нужно сделать — узнать, есть ли среди этих чисел хотя бы один ноль. Пример входных данных для подобной функции выглядит так: l(1, l(5, 0), 10, l(l(8), 3)).
Прежде чем разбирать код, опишем алгоритм, по которому работает функция hasZero:
- Рекурсивно обходим список:
- Если список закончился, а
0не найден, то возвращаемfalse(guard expression). - Если текущий элемент — не список, то проверяем, равен ли он нулю.
- Если равен нулю, то возвращаем
true.
- Если равен нулю, то возвращаем
- Если текущий элемент — список, то запускаем
hasZeroрекурсивно, передав туда текущий элемент.- Если результат этого вызова
true, то возвращаемtrue.
- Если результат этого вызова
- Если не сработали предыдущие терминальные условия, проверяем следующий элемент списка.
- Если список закончился, а
Такой обход дерева называется обход в глубину. Сначала мы опускаемся до самого дна самой левой ветки, затем ветки чуть правее и так далее пока не дойдем до конца.
import { l, cons, head, tail, isEmpty, isList, toString } from '@hexlet/pairs-data';
const hasZero = (list) => {
if (isEmpty(list)) {
return false;
}
const current = head(list);
const rest = tail(list);
if (!isList(current)) {
if (current === 0) {
return true;
}
} else if (hasZero(current)) {
return true;
}
return hasZero(rest);
};
console.log(hasZero(l(1, 3, l(5, l(9), 3), 10))); // => false
console.log(hasZero(l(1, l(l(5, 100), 0), 10))); // => true
https://repl.it/@hexlet/js-sequences-hierarchy-has-zero
Агрегация
Более интересный и сложный пример связан с агрегацией: посчитать количество чего-либо в дереве или собрать список узлов, соответствующий какому-либо критерию. Общий механизм обхода в этих случаях останется абсолютно тем же, но к нему добавится аккумулятор, который нужно прокидывать до самой глубины. По сути, вся задача сводится к реализации рекурсивного reduce. Ниже код функции searchZeros, которая, в отличие от предыдущей реализации, возвращает число нулей в дереве:
import { l, cons, head, tail, isEmpty, isList, toString } from '@hexlet/pairs-data';
const searchZeros = (tree) => {
const iter = (list, acc) => {
if (isEmpty(list)) {
return acc;
}
const current = head(list);
const rest = tail(list);
if (!isList(current)) {
const newAcc = current === 0 ? acc + 1 : acc;
return iter(rest, newAcc);
} else {
return iter(rest, iter(current, acc));
}
};
return iter(tree, 0);
};
console.log(searchZeros(l(1, 3, l(5, l(9), 3), 10))); // => 0
console.log(searchZeros(l(0, l(l(0, 100), 0), 10))); // => 3
https://repl.it/@hexlet/js-sequences-search-zeros
Главное в этом коде находится тут: return iter(rest, iter(current, acc));. Если current список, то прежде чем продолжать проверять список, по которому идет алгоритм, нужно выполнить поиск в найденном поддереве и так далее до самого дна. Соответственно, сначала отработает код iter(current, acc), который вернет acc для поддерева, сложенный с текущим значением аккумулятора. В итоге, на выходе получится новый аккумулятор, который передается дальше.
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
