Обход дерева — Python: Деревья

• Обход в глубину
• Изменение данных

Пошаговый перебор элементов дерева по связям между узлами-родителями и узлами-потомками называется обходом дерева.

Подразумевается, что в процессе обхода каждый узел затрагивается только один раз. По большому счету, все так же, как и при обходе любой коллекции с помощью цикла или рекурсии. Только в случае деревьев способов обхода больше, чем просто «слева направо» и «справа налево».

В этом уроке мы изучим один порядок обхода — обход в глубину, потому что он естественным образом получается при рекурсивном обходе. Об остальных способах можно прочитать в Википедии, либо в рекомендованных Хекслетом книгах.

Обход в глубину

Это один из методов обхода дерева. Стратегия этого поиска состоит в том, чтобы идти вглубь одного поддерева настолько, насколько это возможно.

Этот алгоритм естественным образом ложится на рекурсивное решение и получается сам собой:

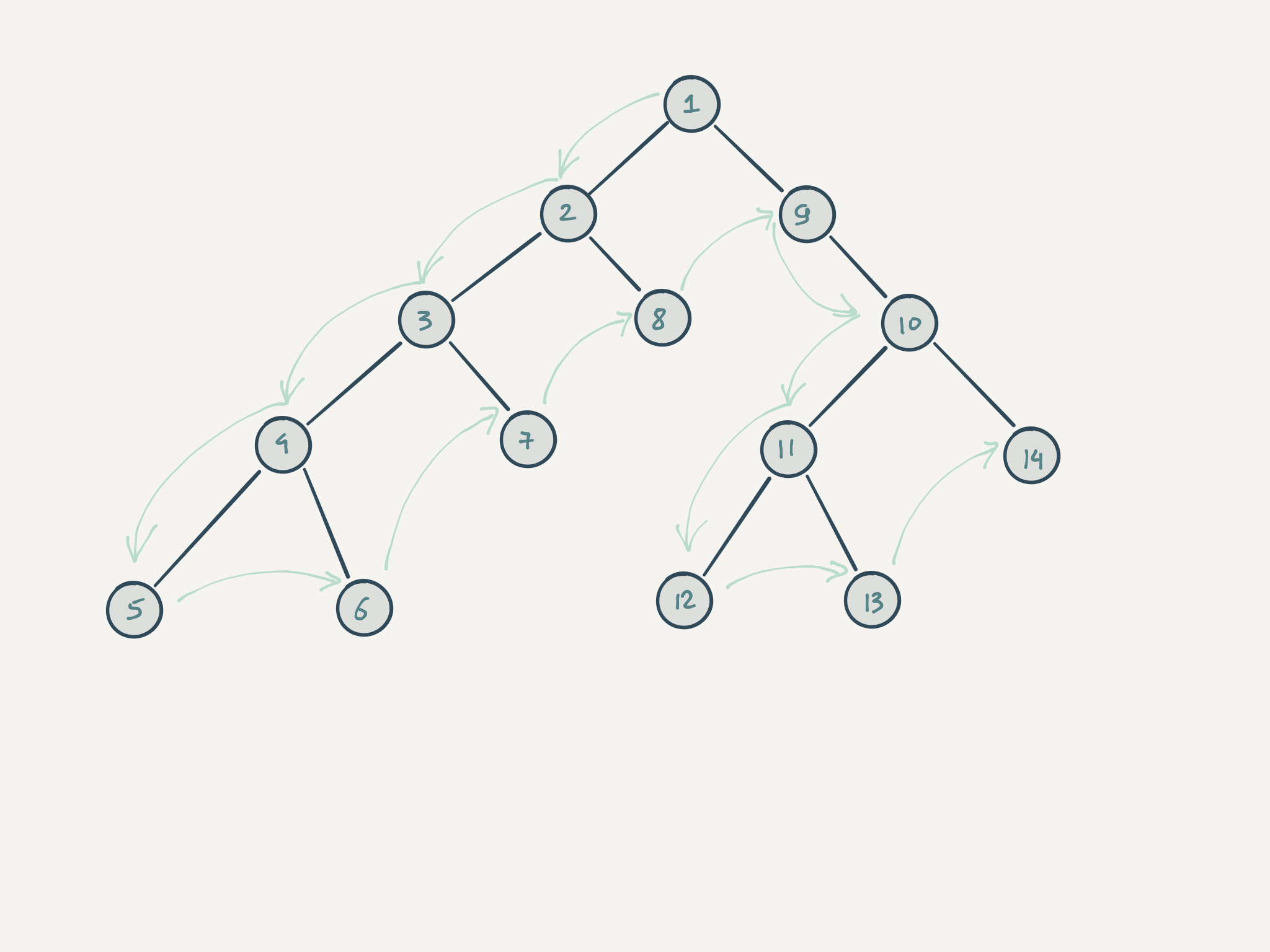
Рассмотрим данный алгоритм на примере следующего дерева:

#     * A
#   / | \
# B * C * D
#  /|   |\
# E F   G J

Каждая нелистовая вершина обозначена звездочкой. Рассмотрим обход этого дерева по шагам:

1. Обход начинается с корневого узла. Проверяем, есть ли потомки у вершины A. Если есть, то запускаем обход рекурсивно для каждого потомка независимо

2. Внутри первого рекурсивного вызова оказывается следующее поддерево:

   # B *
   #  /|
   # E F
   

3. Далее повторяем логику первого шага и проваливаемся на уровень ниже. Внутри оказывается листовой элемент E. Функция убеждается, что у узла нет потомков, выполняет необходимую работу и возвращает результат наверх

4. Снова оказываемся в знакомой ситуации:

   # B *
   #  /|
   # E F
   

   В этом месте рекурсивный вызов запускался на каждом потомке. Первого потомка мы уже посетили, поэтому второй рекурсивный вызов заходит в узел F и выполняет там свою работу. Затем происходит возврат выше, и все повторяется, пока не дойдет до корня:

   from hexlet import fs
   
   tree = fs.mkdir('/', [
       fs.mkdir('etc', [
           fs.mkfile('bashrc'),
           fs.mkfile('consul.cfg'),
       ]),
       fs.mkfile('hexletrc'),
       fs.mkdir('bin', [
           fs.mkfile('ls'),
           fs.mkfile('cat'),
       ]),
   ])
   
   def dfs(node):
       # Распечатываем имя узла
       print(fs.get_name(node))
       # Если это файл, то возвращаем управление
       if fs.is_file(node):
           return
   
       # Получаем потомков
       children = fs.get_children(node)
   
       # Применяем функцию dfs ко всем элементам-потомкам
       # Множество рекурсивных вызовов в рамках одного вызова функции
       # называется древовидной рекурсией
       list(map(dfs, children))
   
   dfs(tree)
   # => /
   # => etc
   # => bashrc
   # => consul.cfg
   # => hexletrc
   # => bin
   # => ls
   # => cat
   

   https://repl.it/@hexlet/python-trees-traversal-dfs

В примере выше печать на экран — это лишь демонстрация. В реальности нас интересует либо изменение дерева, либо агрегация данных по нему. Агрегацию данных рассмотрим позже, а сейчас разберем изменение.

Изменение данных

Допустим, мы хотим реализовать функцию, которая меняет владельца для всего дерева, то есть всех директорий и файлов.

Для этого нам придется соединить две вещи:

• Рекурсию, разобранную выше
• Код обновления узлов из прошлого урока

Так это выглядит в коде:

import copy
from hexlet import fs


def change_owner(node, owner):
    name = fs.get_name(node)
    new_meta = copy.deepcopy(fs.get_meta(node))
    new_meta['owner'] = owner
    if fs.is_file(node):
        # Возвращаем обновленный файл
        return fs.mkfile(name, new_meta)
    children = fs.get_children(node)
    # Ключевая строчка
    # Вызываем рекурсивное обновление каждого потомка
    new_children = list(map(lambda child: change_owner(child, owner), children))
    new_tree = fs.mkdir(name, new_children, new_meta)
    # Возвращаем обновленную директорию
    return new_tree

# Эту функцию можно обобщить до map — отображения, работающего с деревьями

https://repl.it/@hexlet/python-trees-traversal-change-owner

Ключевое отличие от первого примера — вместо печати на экран формируются новые узлы и возвращаются наружу. В конце концов, из них собирается новое дерево.

Все, что мы будем делать дальше по ходу курса, неизменно базируется на этом алгоритме. Попробуйте открыть редактор на своем компьютере и самостоятельно реализовать эту функцию без подглядывания. Так вы убедитесь в том, что поняли эту тему.

---

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты