Python: Абстракция с помощью данных
Теория: Уровневое проектирование
В этом уроке мы рассмотрим еще одну систему — рациональные числа и операции над ними, а также научимся видеть барьеры абстракции и выделять слои.
Рациональное число
Рациональным называют число, которое может быть представлено в виде дроби a/b, где а — это числитель дроби, b — знаменатель дроби. Причем b не должно быть нулем, так как делить на нуль нельзя.
Рациональные числа в Python не поддерживаются, поэтому абстракцию для них создадим самостоятельно. Нам понадобятся конструктор и селекторы:
С помощью трех функций мы определили рациональное число. Конструктор собирает его из частей, селекторы позволяют извлечь каждую часть. Чем при этом является num с точки зрения языка — не важно. Это может быть функция, список или словарь. Во внутренней реализации можно использовать даже строки:
Мы научились представлять рациональные числа, но эта абстракция малоприменима. Она становится полезна, когда появляется возможность оперировать ей.
Для рациональных чисел базовыми операциями можно считать арифметические, например, сложение, вычитание или умножение. Умножение рациональных чисел — самая простая операция. Для ее выполнения нужно перемножить числители и знаменатели:
Если предположить, что реальная структура рационального числа выглядит так: {"numer": 2, "denom": 3}, то решение может быть таким:
С точки зрения вызывающего кода абстракция сохранена. На вход в multiply_rational подаются рациональные числа, на выходе — рациональное число. Но внутри абстракции нет, так как обращение с рациональными числами строится на основе знания их устройства.
Чтобы изменить внутреннюю реализацию рациональных чисел, придется переписать все операции, которые работают с рациональными числами напрямую — то есть без селекторов или конструктора. Данный код нарушает принцип одного уровня абстракции — single layer abstraction.
Уровневое проектирование
При разработке сложных систем используется подход — уровневое проектирование. В его случае системе придается структура с помощью последовательных уровней. Каждый из уровней строится путем комбинации частей, которые на данном уровне рассматриваются как элементарные. Части, которые строятся на каждом уровне, работают как элементарные на следующем:
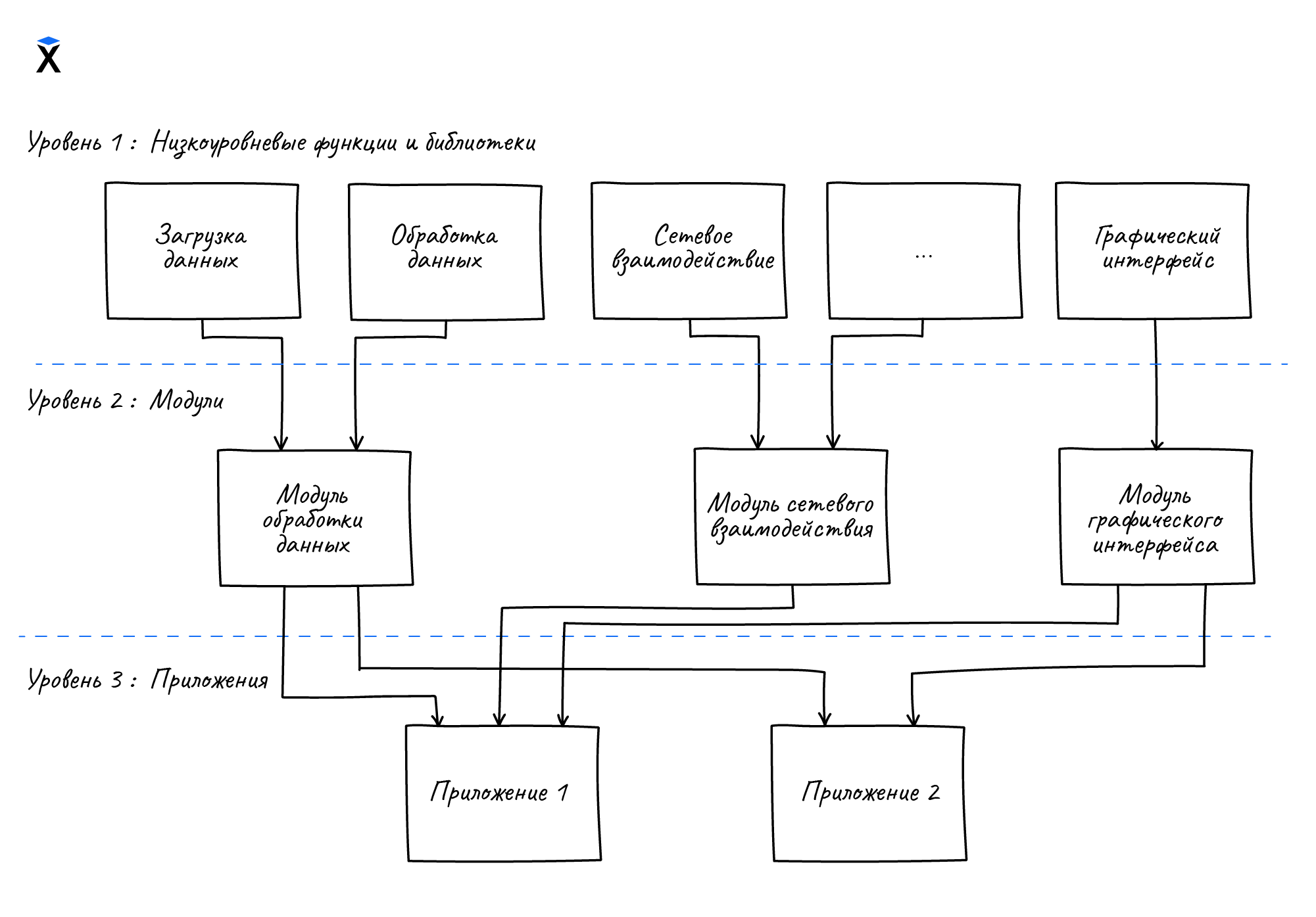
Уровневое проектирование проходит через всю технику построения сложных систем. Например, в разработке программного обеспечения уровневое проектирование может начинаться с создания низкоуровневых функций и библиотек, которые решают конкретные задачи. К таким задачам могут относиться обработка данных, сетевое взаимодействие или графический интерфейс.
Затем эти функции и библиотеки объединяются для создания модулей, которые предоставляют более высокоуровневые возможности. Модули можно использовать, чтобы построить полноценные приложения, которые включают большое количество функциональных возможностей и обеспечивают решение более крупных задач.
Посмотрим на пример кода:
Здесь базовым уровнем являются типы, которые встроены в сам язык: числа и словарь. На их основе сформирован уровень для представления рациональных чисел: make_rational, get_denom, get_numer. Затем — уровень, на котором реализованы арифметические операции над рациональными числами: сложение, вычитание, умножение и так далее.
Речь идет про реализацию самих уровней. Например, операция сложения полностью опирается на конструктор и селекторы, но ничего не знает и не может знать про внутреннее устройство самих рациональных чисел. С другой стороны, это не значит, что в одном месте не могут появиться функции из разных уровней. Это нормально во многих случаях. Например:
Выводы
В этом уроке мы рассмотрели еще одну систему — рациональные числа и операции над ними. Так как в Python рациональные числа не поддерживаются, нам предстояло самостоятельно создать для них абстракцию.
Также мы разобрались, как видеть барьеры абстракции и выделять слои. Мы узнали, что такое уровневое проектирование. Оно применяется при разработке сложных систем и проходит через всю технику их построения.

