Оценка Big O — PHP: Массивы

Когда мы говорим об алгоритмах, нельзя не упомянуть их сложность. Она обозначается как Big O и указывает, насколько эффективен тот или иной алгоритм.

Как вы помните, есть много алгоритмов сортировок. Они выполняют одну и ту же задачу, но при этом у них разная сложность — то есть количество выполняемых операций алгоритмом для достижения своей цели. Разные способы сортировки требуют очень разного количества проходов по массиву. Конкретное количество операций зависит от входных данных — например, для уже отсортированного массива количество операций будет минимальным (но они все равно будут, потому что алгоритм должен убедиться в том, что массив отсортирован).

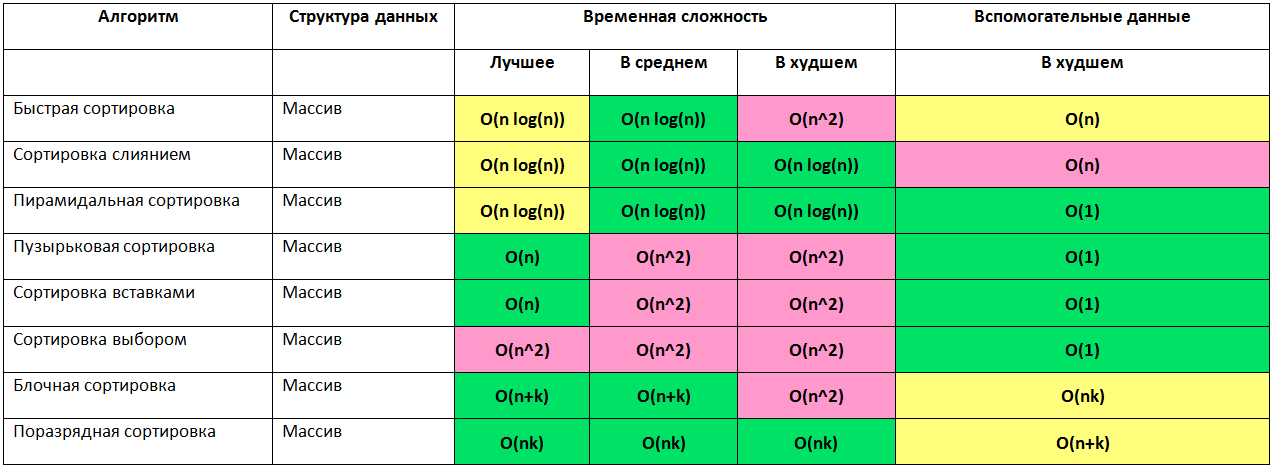
Big O показывает, насколько увеличится количество операций при увеличении объема данных. Рассмотрим пару примеров:

Что такое «худший случай»? Количество операций будет разным даже при работе с массивами одного размера — все зависит от состояния начального массива.

Проведем аналогию с кубиком Рубика. Чтобы его собрать, нужно провести какое-то количество действий. Их число зависит от положения, в котором находятся его грани перед сборкой. В некоторых случаях действий понадобится мало, в других — много. Худшим случаем называется ситуация, при которой нам понадобится максимальное количество действий.

Алгоритмическая сложность всегда оценивается по худшему случаю для выбранного алгоритма.

Для еще одного примера вспомним вложенные циклы и поиск пересечений в неотсортированных массивах.

Для каждого элемента из одного массива мы проверяем каждый элемент другого массива. При этом мы используем либо цикл, либо функцию in_array() со сложностью — в худшем случае мы просмотрим весь массив.

Если размеры обоих массивов одинаковы и равны , то поиск пересечений имеет квадратичную сложность .

Одни алгоритмы эффективные, другие — не очень. Скорость работы неэффективных алгоритмов заметно падает даже при небольшом количестве элементов. Эффективные алгоритмы работают быстрее, и при этом они нередко потребляют больше памяти или запускаются параллельно. Часто в программировании эффективность — это компромисс. Выигрывая в одном месте, мы проиграем где-то в другом.

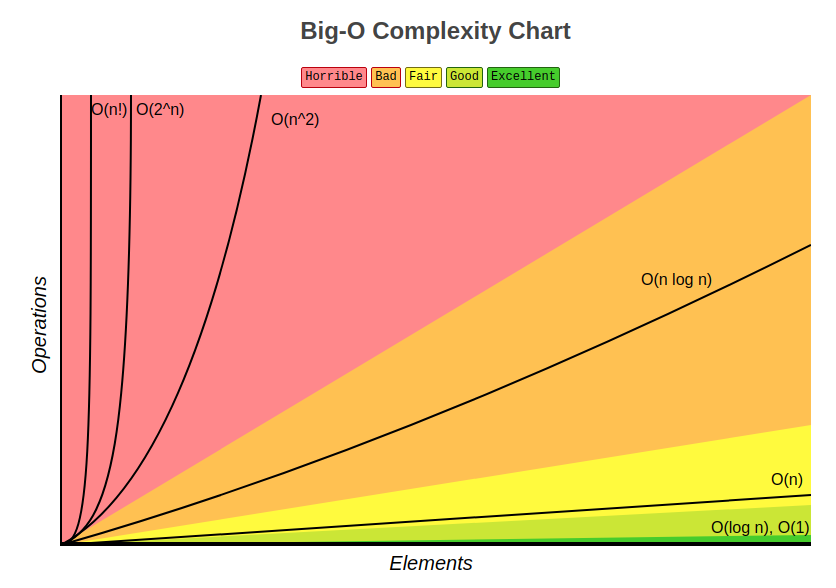
Во многом, Big O — это теоретическая оценка, на практике все может быть по-другому. Реальное время выполнения зависит от множества факторов, в том числе архитектуры процессора, операционной системы, языка программирования и типа доступа к памяти.

Вопрос эффективности кода довольно опасен. Например, в университетах программирование обычно изучают, начиная с алгоритмов. Из-за этого студентам может казаться, что эффективность — это главное, ведь код должен работать быстро. Такой подход приносит больше вреда, чем пользы. Дело в том, что эффективный код всегда сложнее неэффективного. Этот сложный код больше подвержен ошибкам, его труднее писать и модифицировать.

На практике настоящая эффективность нужна только в редких случаях. Обычно тормозит не код, а запросы к базе данных, сеть или что-то другое. Если конкретный участок кода выполняется медленно, это не всегда критично. Вполне возможно, что этот код работает с небольшим объемом памяти, вызывается все один раз и ни на что не влияет. К реальному замедлению может приводить совершенно другой фрагмент кода, который вызывается тысячи раз.

Перед тем, как пытаться что-то оптимизировать, обязательно прочитайте небольшую онлайн-книгу, которая хорошо объясняет суть всех оптимизаций.