Математики по опыту знают, что все нужно подвергать строгой проверке, даже самые очевидные аргументы и утверждения. Интуиция и невнимательность часто могут сбить с пути и привести к неверным выводам, например:
- Сидящий человек встал со стула
- Если человек встал, значит его можно считать стоящим
- Следовательно, сидящий человек стоит
По логике все верно, но разве можно сидеть и стоять одновременно?
Подобные ошибки иногда ускользают даже от самого бдительного глаза. Они называются математическими уловками или софизмами. С их помощью можно прийти к выводам, которые противоречат математическим законам и здравому смыслу.
Можно найти убедительное доказательство, что:
- Все люди на планете одного возраста
- Числа 5700 и 57 равны
В этом уроке мы поговорим о софизмах подробнее и научимся отыскивать ошибки в них.
Что такое софизмы
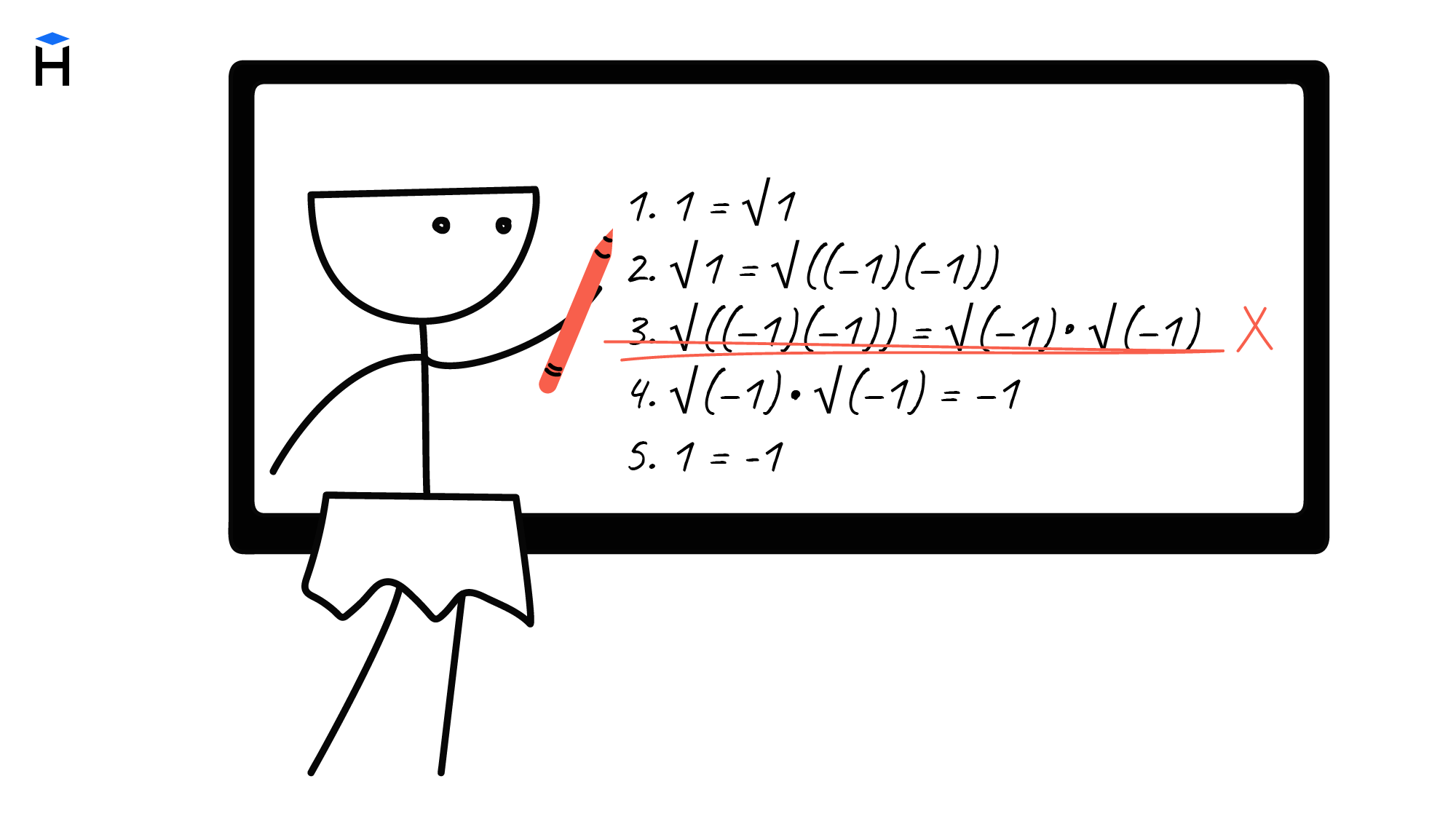
Софизмы — это неверный результат, который мы получаем в результате внешне правильных, но умозрительных рассуждений. Посмотрим, как софизмы работают на практике. Попробуем доказать, что 1 = -1:
1 = sqrt(1)sqrt(1) = sqrt(((-1)(-1)))sqrt((-1)(-1)) = sqrt(-1)*sqrt(-1)sqrt(-1)*sqrt(-1) = -11 = -1
С первого взгляда все правильно. Где же ошибка? Она кроется на третьем шаге:
sqrt((-1)(-1)) = sqrt(-1)*sqrt(-1)
В математике есть правило, по которому sqrt(ab) = sqrt(a)*sqrt(b). Но данное правило не работает, если a и b отрицательны — в нашем примере как раз такой случай. Таким образом, из-за одного ошибочного утверждения все доказательство из пяти шагов становится неверным.
Посмотрим на еще один пример. Здесь мы доказываем, что 1 доллар равен 1 центу:
- 1 доллар = 100 центов
- 100 центов = 10 центов × 10 центов
- 10 центов × 10 центов = 0.1 доллара × 0.1 доллара
- 0.1 доллара × 0.1 доллара = 0.01 доллара
- 0.01 доллара = 1 доллар
Это доказательство неверно, потому что в шагах нарушены правила действий с размерностями. Если мы возводим величину в квадрат, то по правилу размерность тоже нужно возвести в квадрат: 2 cm xx 2 cm = 4 cm^2. В примере выше этого не происходит: мы возводим в квадрат только значение 0.1, но забываем сделать то же самое с размерностью.
Как найти ошибку в софизме
Чтобы обнаружить заблуждение, нужно рассматривать каждый шаг доказательства по отдельности. Давайте рассмотрим еще один пример:
- Пусть
x = 1 - Домножим обе части на
x:x^2 = x - Вычтем 1 из обеих частей:
x^2 - 1 = x - 1 - Разделим обе части на x-1:
frac((x^2 - 1))(x - 1) = 1 - Разложим левую часть по формуле:
frac(((x - 1)(x + 1)))(x - 1) = 1 - Упростим:
x + 1 = 1 - Вычтем 1 из обеих частей:
x = 0 - Подставим значение
x = 1:1 = 0
Ошибка здесь неочевидна с первого взгляда:
- В шаге 2 умножаем обе стороны уравнения на
x - В шаге 4 происходит деление на
x - 1 - В шаге 7 мы обнаружили, что шаг 2 привел уравнение к виду
x = 0 - Возвращаемся к шагу 4 и видим ошибку:
x - 1 = 0, хотя на ноль делить нельзя
Делаем вывод: именно четвертый шаг приводит к тому, что решение x = 0 остается единственным вариантом.
Аналогичным методом можно доказать, что любое число равно любому другому числу. Например:
- Определим значение переменной:
x = 57000 - Вычтем:
x - 57000 = 0 - Домножим на x + 200:
(x - 57000)(x + 200) = 0 - Разделим на x - 57000:
x + 200 = 0 - Получаем результат:
x = -200
В этом уроке мы разобрались, как искать ошибки в софизмах — нужно пошагово разбирать решение и проходить всю последовательность шагов.
Навык работы с софизмами и их исправления очень важен для всех, кто работает с логикой, математикой и программированием. Он позволяет минимизировать ошибки и повышает качество финального решения.
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
