Нотации — Введение в математическую логику

• Пропозиции
• Операторы
  • Конъюнкция
  • Дизъюнкция
  • Отрицание
  • Импликация
• Комбинации
  • Предикаты
    • Квантификаторы

Как в любом другом языке, в математике есть свои правила, союзы и слова-связки. В алгебре логики они называются нотациями — то есть операциями над высказываниями и выражениями.

В этом уроке мы начнем изучать нотации, рассмотрим основные логические символы и разберемся, как их использовать.

Пропозиции

Пропозиция — это утверждение, которое можно четко определить как истинное или ложное.

Если пропозиция истинна, то ее значение равно true (T). Например:

• Если сложить 1 и 2, то получится 3
• 10 больше, чем 9
• Если число положительное, то его квадрат тоже будет положительным

Если пропозиция ложна, то ее значение равно false (F). Например:

• 11 больше, чем 12
• Любое число является простым числом
• Радиус Земли равен радиусу футбольного мяча

Операторы

В естественном языке мы умеем объединять несколько предложений в одно. Возьмем такой пример:

Высказывание 1: У Ромы есть зеленая рубашка
Высказывание 2: У Васи есть зелёная рубашка

Объединим высказывания через союз «И»:

У Ромы есть зеленая рубашка и у Васи есть зеленая рубашка

А теперь попробуем объединить через союз «ИЛИ»:

У Ромы зелёная рубашка или у Васи есть зелёная рубашка

Для объединения мы используем логические связки — операторы. Всего их четыре:

• Конъюнкция
• Дизъюнкция
• Отрицание
• Импликация

Далее поговорим о них подробнее.

Конъюнкция

Конъюнкция — это оператор, который работает как союз «и» и обозначается через ∧. Вся конъюнкция истинна, только если оба высказывания истинны:

• a: Apple продает смартфоны — true
• b: Apple продает ноутбуки — true
• a ∧ b: Apple продает смартфоны и ноутбуки — true

Бывают случаи, когда одно из высказываний ложное. Тогда вся конъюнкция становится ложной:

• a: Apple продает смартфоны — true
• b: Apple продает яблоки — false
• a ∧ b: Apple продает смартфоны и яблоки — false

Дизъюнкция

Дизъюнкция — это оператор, который работает как союз «или» и обозначается через ∨. Вся дизъюнкция истинна, если истинно одно из высказываний или оба:

• a: Apple продает смартфоны — true
• b: Apple продает яблоки — false
• a ∨ b: Apple продает смартфоны или яблоки — true

Компания Apple действительно продает смартфоны, то есть высказывание a верное. Если в дизъюнкции есть хотя бы одно верное высказывание — вся остальная дизъюнкция тоже верна.

Рассмотрим еще один пример. Здесь вся дизъюнкция ложная, потому что оба высказывания ложные:

• a: Apple продает груши — false
• b: Apple продает яблоки — false
• a ∨ b: Apple продает груши или яблоки — false

Отрицание

Отрицание — это оператор, который работает как частица «не» и обозначается через ¬. Например:

• a: У квадрата четыре стороны — true
• ¬a: У квадрата НЕ четыре стороны — false

Бывают случаи, когда нужно добавить отрицание к отрицанию:

• a: У квадрата НЕ четыре стороны — false
• ¬a: У квадрата НЕ НЕ четыре стороны — true
• (То же самое, что «у квадрата четыре стороны»)

Импликация

Импликация — это оператор, который обозначает условное высказывание. Она работает как конструкция «если..., то...» и обозначается через →.

Вот несколько примеров условных высказываний:

• Если пойдет дождь, я останусь дома
• Если ты получишь диплом, то сможешь найти работу
• Если машина уехала, значит, Вася уехал

Может возникнуть путаница: когда импликацию следует считать истинной, а когда — ложной?

Чтобы решить этот вопрос, рассмотрим пример. Предположим, что Вася будет играть в теннис с Ромой. Рома делает заявление:

Если ты выиграешь, я куплю тебе мороженое

Если Вася выиграет, то он получит мороженое. Но если Вася проиграет, Рома ничего не должен — обещаний на этот случай он не давал.

В конце матча возможны четыре варианта развития событий:

• (1) Вася побеждает — получает мороженое
• (2) Вася побеждает — не получает мороженое
• (3) Вася проигрывает — получает мороженое
• (4) Вася проигрывает — не получает мороженое

Заявление Ромы прямо исключает вариант (2). Еще Рома не упомянул (3) или (4) — если Вася проиграет, Рома может поступить как угодно.

По сути, Рома сказал, что события (1), (3) и (4) могут произойти, а (2) не произойдет. Рома будет пойман на лжи, только если произойдет исход (2). В остальных трех случаях он скажет правду.

Чтобы записать высказывание Ромы символически, определим более простые высказывания:

• a: ты выиграл
• b: я куплю тебе мороженое

Используем логический символ импликации →. Направим его от a к b, чтобы сформировать составное высказывание:

a → b: Если ты выиграешь, то я куплю тебе мороженое

Эта импликация ложна только в одном случае:

• Когда a истинно, а b ложно — то есть Вася выиграл, но не получил мороженое

При всех других исходах утверждение истинно.

Обозначим эту ситуацию через логические уравнения для импликации:

• (1) Вася побеждает и получает мороженое — T → T = T
• (2) Вася побеждает и не получает мороженое — T → F = F
• (3) Вася проигрывает и получает мороженое — F → T = T
• (4) Вася проигрывает и не получает мороженое — F → F = T

Комбинации

Допустим, у нас есть два высказывания, оба могут быть истинными или ложными:

• Если оба высказывания истинны, то мы получим комбинацию true true: верно и первое, и второе. Будем обозначать такие случаи T T
• Если верно только первое высказывание, то получаем комбинацию true false: первое верно, второе неверно. Обозначаем как T F

Таким образом, в этом примере возможны четыре комбинации, каждая представлена одним из логических операторов:

• T T — Конъюнкция
• T F — Дизъюнкция
• F T — Отрицание
• F F — Импликация

Объединим эти высказывания и составим новую пропозицию. Она тоже может быть истинной или ложной, поэтому мы получим (2⁴⁾ возможных комбинаций из T и F.

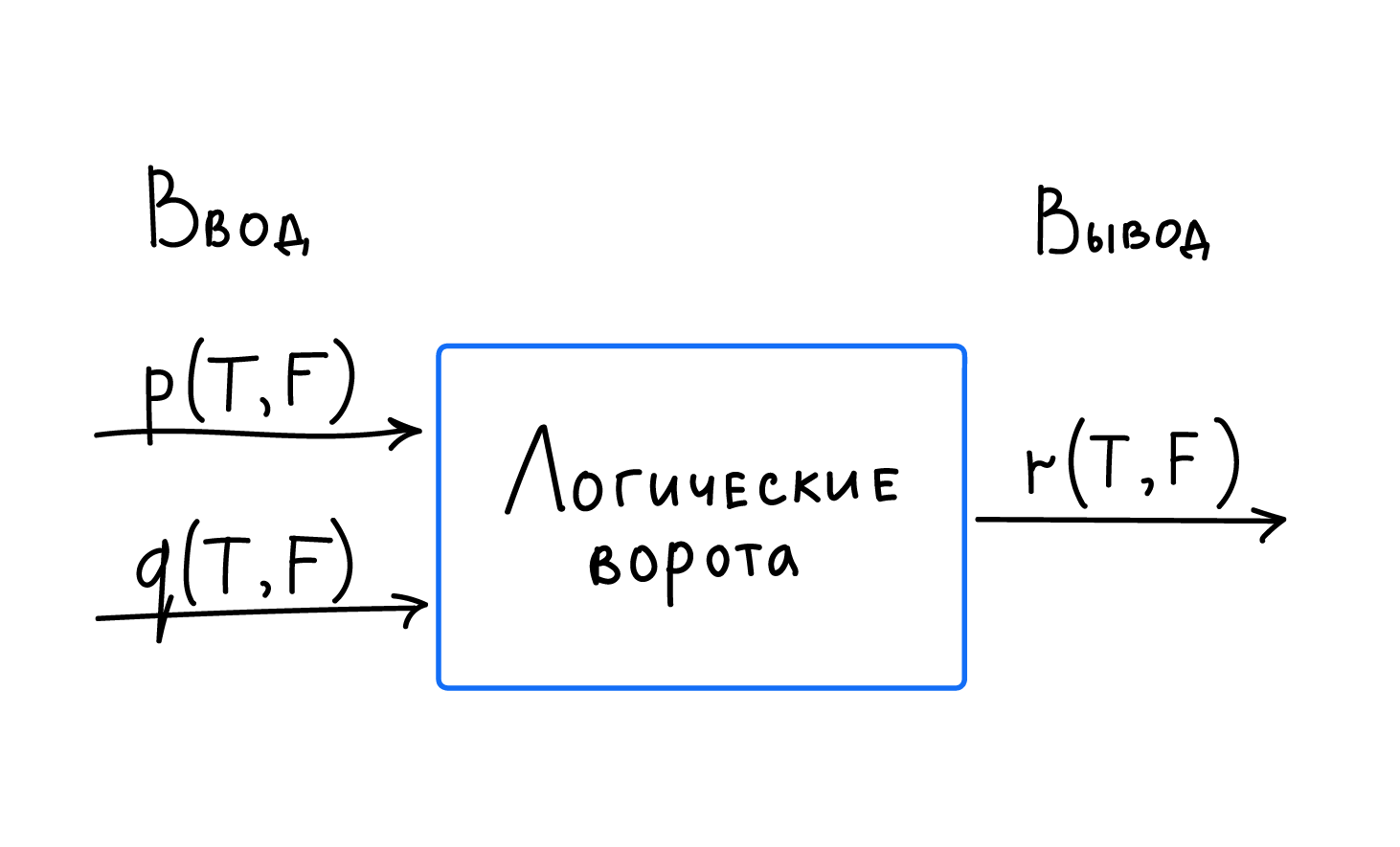
На схеме ниже видно, как новая пропозиция составляется из двух высказываний:

Предикаты

Выше мы рассматривали только пропозиции — утверждения, которые могут быть либо истинными, либо ложными. Теперь попробуем расширить простую пропозициональную логику и введем новое понятие.

Предикат — это логическое утверждение, в котором содержатся переменные. Предикаты обозначаются заглавной буквой, а переменные перечисляются как аргументы. Например, предикат P с переменной x обозначается так: P(x).

Как определить, предикат истинный или ложный? Это зависит от значения его переменных. Рассмотрим на примерах:

• Задаем предикат: P(x): x — это дерево
• Определяем значение переменной: x = береза
• Получаем истинное высказывание: P(береза): береза — это дерево
• Определяем еще одно значение переменной: x = ромашка
• Получаем ложное высказывание: P(ромашка): ромашка — это дерево

И еще один пример:

• Задаем предикат: P(x): x — это дерево или цветок
• Определяем значение переменной: x = береза
• Получаем истинное высказывание: P(береза): береза — дерево или цветок
• Определяем еще одно значение переменной: x = ромашка
• Получаем истинное высказывание: P(ромашка): ромашка — это дерево или цветок
• Определяем еще одно значение переменной: x = смартфон
• Получаем ложное высказывание: P(смартфон): смартфон — это дерево или цветок

Предикаты принимают два значения — истина или ложь. Поэтому к ним применимы все операторы алгебры логики, которые мы рассмотрели выше. Используя операторы, можно формировать более сложные предикаты.

Квантификаторы

Существует еще одна операция с предикатами — квантификация. Квантификация помогает определить степень достоверности предиката — то есть диапазон значений переменных, для которых предикат должен выполняться. В логике предикатов есть два типа квантификаторов.

Универсальный квантификатор (∀) похож на слово «каждый» и передает такое значение:

«Предикат P(x) истинен для каждого значения переменной определенной области»

Экзистенциальный квантификатор (∃) похож на слово «существует» и передает такое значение:

«Существует такое значение переменной, при котором P(x) истинно»

Предикаты, логические операторы и квантификаторы — это мощные инструменты, которые помогают описывать математические объекты и моделировать реальный мир. В этом уроке мы раскрыли не всю полноту использования операторов. Более подробно рассмотрим их далее в курсе.

Операторы и связки еще будут встречаться в курсе. Чтобы их не забыть, обращайтесь к таблице:

---

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты