Деревья — Теория графов

• Деревья
• Листья и индукция
• Альтернативные определения деревьев
• Леса
• Выводы

В этом уроке мы изучим еще один вид графов — древовидные. Именно этот вид графов активно используется в программировании — он связан с алгоритмами сортировки и поиска.

Деревья

Деревья — это связные графы без циклов. Их часто применяют в математике и информатике. Вот так они выглядят:

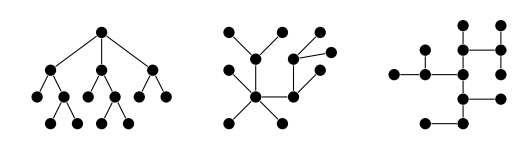
Как видно из примера, у деревьев определенная древовидная ветвистость, откуда они и получили свое название.

Благодаря связности и отсутствию циклов у деревьев есть ряд свойств:

• В любом дереве есть ровно один путь из каждой вершины в каждую другую. Например, если есть два пути к вершине, то их можно объединить, чтобы получить цикл
• У деревьев наименьшее количество ребер, которое только может быть у графа. При этом они остаются связными. Каждое ребро дерева — режущее, значит, не лежит в цикле
• У деревьев наибольшее число ребер, которое может быть у графа без циклов. Добавление любого ребра к дереву создает ровно один цикл. Например, если добавить ребро между вершинами u и v, то получится цикл, включающий ребро uv и путь. Он гарантированно существует между u и v

Листья и индукция

С древовидными графами работает механизм индукции — это значит, что по каждому дереву с n вершинами можно перемещаться с шагом n-1 ребро.

Для этого нам понадобится лист в дереве — вершина, которая находится на концах каждого дерева.

Разберем следующую теорему: у каждого дерева с хотя бы двумя вершинами есть хотя бы два листа. Докажем это утверждение.

Рассмотрим любой путь максимальной длины в дереве. Поскольку у дерева две вершины и оно связное, этот путь должен существовать. У обеих конечных точек этого пути степень 1 в дереве. Их единственные соседи — вершины, которые располагаются перед ними на пути.

Обсудим, почему это работает именно так:

• У конечных точек не может быть других соседей на пути, поскольку это создало бы цикл, что невозможно в дереве
• У конечных точек не может быть других соседей вне пути, поскольку тогда мы могли бы использовать такого соседа для расширения пути. Только это невозможно, так как у пути уже максимальная длина

Воспользуемся индукцией, чтобы доказать, что каждое дерево с n вершинами имеет n - 1 ребро.

Предположим, что все деревья на n вершинах содержат n - 1 ребро. Пусть T — дерево на n + 1 вершинах. У T есть лист v. У графа T - v n вершин. При этом он является деревом, потому что удаление вершины не может создать цикл, а удаление листа не может разорвать граф.

По гипотезе индукции T - v имеет n - 1 ребер. Чтобы получить T - v из T было удалено одно ребро, у T должно быть n ребер. Таким образом, результат индукции верен. Такую же технику можно использовать в доказательствах с участием других деревьев.

Альтернативные определения деревьев

Любое из свойств дерева используют, чтобы переформулировать определение дерева.

Для графа T эквивалентны следующие утверждения:

1. T — дерево
2. Каждая пара вершин графа T соединена ровно одним путем
3. T связно, и удаление любого ребра разъединяет его
4. У T нет циклов, и добавление любого ребра создает цикл
5. T — связный граф с n вершинами и n-1 ребрами
6. T — ациклический граф с n вершинами и n-1 ребром

Доказательство любой части этого определения включает аргументы, аналогичные тем, которые мы приводили выше. Существуют и другие способы комбинирования свойств деревьев для получения альтернативных характеристик деревьев.

Леса

Если мы уберем связность из определения дерева, то получим лес — граф, в котором нет циклов. Он состоит из нескольких компонентов — деревьев:

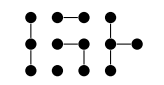
Деревья и леса — двучленные, то есть у них нет циклов.

Выводы

У деревьев много применений, особенно в информатике. В ней основное внимание уделяется деревьям с корнями. В таких деревьях одна вершина обозначается как корень, и от нее дерево растет наружу. При корнях нужно рассматривать вершины как родителей других вершин, как в семейном дереве.

Еще есть бинарные деревья, в которых у каждой вершины не более двух дочерних вершин. Бинарные деревья важны во многих алгоритмах информатики, таких как поиск, сортировка и разбор выражений.