Обычно нам нужно добраться из любой вершины в любую другую и использовать как можно меньше ребер. При этом часто возникает проблема поиска связного подграфа графа, в котором используется как можно меньше ребер. Чтобы избежать этой проблемы, нужно использовать связные деревья.
В этом уроке мы продолжим изучать древовидные графы и разберем деревья разветвления. Вы узнаете, какие методы подсчета применяются в работе с такими деревьями и как подобные графы помогают решать задачи в программировании.
Что такое остовные деревья
Наличие цикла в подграфе означает, что у нас есть лишнее ребро, поэтому нам не нужны никакие циклы. Так мы ищем связный подграф без циклов, который включает в себя все вершины исходного графа. Такой граф называется связным деревом.
Ниже показаны два графа со связными деревьями:
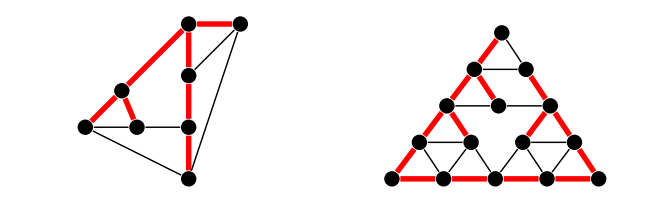
Есть еще отдельный вид деревьев — остовные (spanning trees). Они получаются, если из исходного графа удалить максимальное число ребер, входящих в циклы, но при этом не нарушать связность графа.
Такие деревья активно применяются в информатике — например, так устроена маршрутизация пакетов в компьютерной сети. Допустим, у нас есть несколько компьютеров, объединенных в сеть. Если представить их в виде графа, то компьютеры становятся вершинами, а прямые соединения между двумя компьютерами — ребрами.
Когда один компьютер хочет отправить пакет информации другому, этот пакет передается между компьютерами в сети, пока не попадет в пункт назначения. Этот процесс называется маршрутизацией.
Циклы в этой сети могут привести к тому, что пакет будет вечно перемещаться по сети. Поэтому на каждом из компьютеров выполняется алгоритм, направленный на поиск дерева разветвления — подграфа сети, в котором позволяет добраться от любого компьютера к другому без циклов.
Есть удобный способ найти дерево разветвления в графе. Для этого используют небольшую вариацию алгоритмов DFS/BFS, которые мы рассматривали ранее.
Сначала нам нужно построить дерево. Затем мы видим вершину и добавляем ее в дерево вместе с ребром, связанным с ней, от текущей искомой вершины. Если мы видим вершину снова при поиске от другой вершины, мы не добавляем ребро в этот раз.
Получается, что мы проходим по графу и добавляем ребра, которые не вызывают циклов, пока не достигнем всех вершин. Альтернативный подход — удалить ребра из графа до тех пор, пока не останется циклов, при этом граф всегда должен оставаться связным.
Подсчет прямых деревьев
Чтобы обозначить количества прямых ребер графа , будем использовать обозначение . Также для подсчета нам нужен новый термин — охватывающее дерево неориентированного графа . Так называют подграф графа , который является деревом и содержит все вершины из .
Если — дерево, то = 1, а . Это следует из того, что удаление любого из ребер цикла создает другое охватывающее дерево. Если удалить более чем одно ребро, то дерева не станет.
Если у графа есть вершина разреза, то она разделяет его на две части:
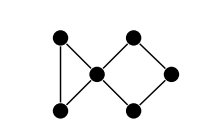
У охватывающих деревьев двух частей нет никакого взаимодействия, кроме как через эту вершину. Поэтому мы можем получить общее число охватывающих деревьев, если перемножим числа охватывающих деревьев по обе стороны от вершины разреза, что дает .
Одна из формул для определения количества охватывающих деревьев называется сокращением ребра. Сжатие — это когда мы сжимаем ребро до одной точки, где ребро удаляется, а две его конечные точки сводятся к одной вершине.
Ниже показаны два примера, где ребро сжимается в новую вершину :
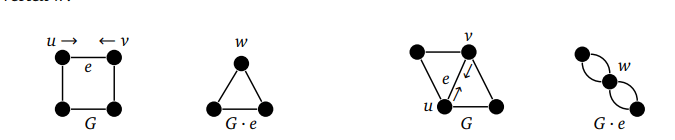
Предположим, что — это граф с ребром . Тогда сокращение в — это операция, создающая новый граф, который обозначается . У такого графа те же вершины и ребра, что и . Но есть одно исключение: и заменяются новой вершиной . Она смежна со всеми соседями и в .
Так получается следующая формула для числа прямых деревьев графа :
Прямые деревья такие же, как и прямые деревья , которые не содержат . считает прямые деревья , которые содержат . Любое такое прямое дерево должно включать новую двойную вершину . Это соответствует включению ребра в оригинал, так как новая двойная вершина стоит на месте и его двух конечных точек.
Например, нам нужно вычислить количество прямых деревьев :
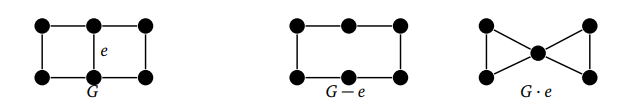
Если убрать из среднее ребро , мы получим . Любые пять ребер графа образуют охватывающее дерево графа , поэтому существует шесть охватывающих деревьев графа . Сжатие среднего ребра из дает нам граф-бабочку, показанный выше.
Любое прячущее дерево должно включать два ребра из левой половины графа и два ребра из правой. Есть три способа включить два ребра слева и три способа включить два ребра справа, поэтому существует девять возможных прямых деревьев. Таким образом, всего в мы имеем .
В общем случае эта формула дерева расплетения может быть применена рекурсивно. То есть, мы разбиваем на и , затем разбиваем каждый из них еще больше, пока не дойдем до графов, чьи прямые деревья мы можем легко сосчитать. Для больших графов это быстро выйдет из-под контроля, потому что количество графов растет экспоненциально.
В этом уроке мы познакомились с остовными деревьями и научились правилам подсчета. Эти знания помогаю понять, как устроены структуры данных и компьютерные сети.
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
