Теория: Взвешенный граф

В этом уроке разберем, что такое взвешенный граф и для чего он полезен. Также познакомимся с алгоритмом Крускала, и рассмотрим, как и почему он работает.

Что такое взвешенный граф

Взвешенный граф — это граф, в котором каждое ребро обозначается числом. Это число — его вес:

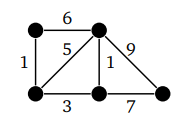
Вес — это стоимость использования данного ребра. Например, приведенный выше граф может представлять дорожную сеть, где вершины — это города, ребра — дороги между ними, а вес — стоимость строительства этих дорог.

Предположим, что мы хотим построить дороги, чтобы добраться из одного города в другой. Нам нужно сделать это как можно дешевле. Так может выглядеть ответ:

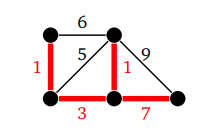
В этом случае нам не нужны циклы, так как мы пытаемся сделать все как можно дешевле. Мы хотим добираться до любой вершины графа, поэтому нам нужно минимальное охватывающее дерево, в котором сумма весов всех ребер в дереве как можно меньше.

Существует несколько алгоритмов, чтобы найти минимальные остовные деревья. В этом уроке мы рассмотрим алгоритм Крускала.

Что такое алгоритм Крускала

Алгоритм Крускала строит охватывающее дерево графа G по одному ребру за раз. На каждом шаге алгоритма мы берем ребро G с таким весом, чтобы добавление этого ребра в строящееся дерево не создавало цикла.

Мы можем разрывать связи между весом ребер как угодно, или добавлять ребра до тех пор, пока это не станет невозможным. В графе с n вершинами нам всегда потребуется добавить ровно n - 1 ребро.

Так это выглядит (грани выделены в порядке их добавления):

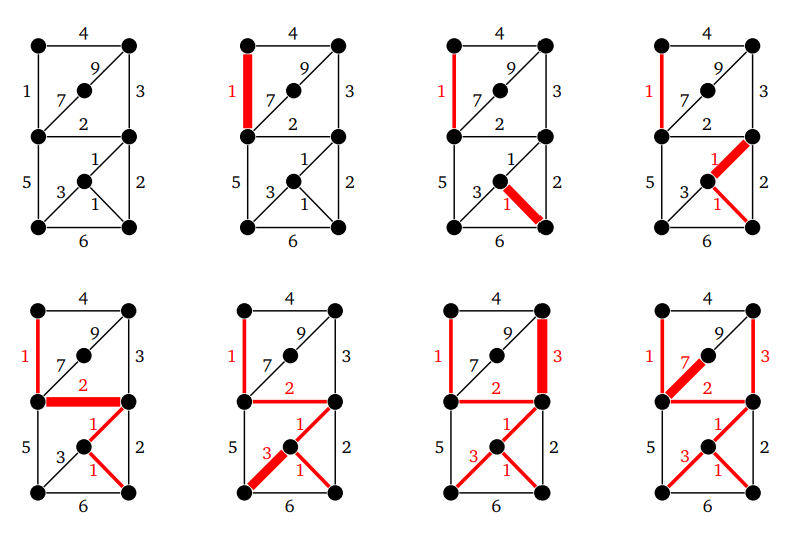
С помощью алгоритма Крускала на каждом шаге выбирается самое дешевое доступное ребро. В этом случае не нужно задумываться о будущих последствиях этого выбора. Эта стратегия всегда дает минимальное остовное дерево.

Почему алгоритм Крускала работает

Разберем несколько причин, почему граф T, который строит алгоритм Крускала, действительно остовное дерево графа:

1. У T нет циклов, поскольку алгоритм Крускала не может их создать
2. T — связной граф, иначе мы могли бы добавить ребро между компонентами T без цикла
3. T — охватывающий граф, который включает каждую вершину. Иначе мы могли бы добавить ребро из T в вершину, которая не входит в T, не вызывая цикла
4. Мы знаем, что у деревьев на n вершинах всегда n-1 ребро, поэтому нам нужно добавить ровно n - 1 ребро

Теперь рассмотрим, почему у дерева Крускала T — минимальный вес. Представим минимальное расходящееся дерево S, которое не равно T. Когда мы проходим через процесс Крускала и добавляем ребра, мы добавляем в T ребро e, которое не является частью S.

Предположим, мы попытаемся добавить e в S. Это создаст цикл по основным свойствам деревьев. Вдоль этого цикла должно быть еще какое-то ребро d, которого нет в T. T — это дерево, и оно не может содержать все ребра этого цикла.

В этом примере показана гипотетическая часть S вместе с d и e:

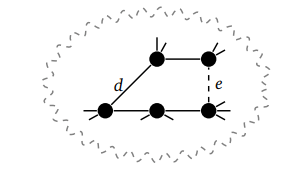
Теперь удалим d из S и заменим его на e — это дерево S - d + e. Если просто менять одно ребро цикла на другое, S - d + e все равно прямое дерево G.

Процесс Крускала добавил ребро e, а не d. Это означает, что вес e меньше или равен весу d. Это делает S - d + e минимальным прямым деревом G, которое согласуется с T на одно ребро больше, чем S.

Мы можем повторять этот процесс, пока не получим минимальное остовное дерево, которое согласуется с T по каждому ребру. Это означает, что T должно быть минимальным остовным деревом.

Выводы

Мы разобрались, что такое взвешенный граф и для чего он полезен. Также познакомились с алгоритмом Крускала, и поняли, почему он работает. Написать код, который реализует алгоритм Крускала, несложно. Самое сложное — проверить, не создает ли добавление ребра цикл. Например, это можно сделать с помощью структуры данных disjoint set.