Теория графов
Теория: Связанность
В этом уроке мы разберемся со связными подграфами, а также узнаем, что произойдет, если связный заменить на двусвязный.
Определения и свойства связности в графах
Связность графа — это существование пути от любой вершины к любой другой. При этом некоторые графы более связны, чем другие. Например, дерево является минимально связным, потому что удаление любой вершины или ребра из дерева приводит к его разъединению. Обратный пример — это полный граф, потому что он очень хорошо связан.
Раз степень связанности может меняться, значит нам нужен способ ее измерить. Обычно смотрят, сколько вершин или ребер нужно удалить, чтобы разъединить граф.
Граф называется k-связным, если для его рассоединения нужно удалить не менее k вершин. Связность неполного графа G обозначается как k(G) — это минимальное число вершин, которые нужно удалить, чтобы граф был разомкнут.
Граф называется k-краевым связным, если для его рассоединения требуется удалить не менее k ребер. В этом случае связность графа G обозначается κак 0 (G) — это минимальное число ребер, которые нужно удалить, чтобы граф был разомкнут.
Связность полного графа K_n — это особый случай. По условию, k(K_n) = n - 1.
Есть разница между связностью k и k-связностью:
- Граф со связностью
3может быть односвязным, двусвязным и трехсвязным - Связность
kговорит о максимальномk, при котором граф —k-связный - У несвязного графа связность равна
0 - Связность графа равна
1, когда у него есть разрезанная вершина или разрезанное ребро - У двусвязного графа нет разрезанной вершины или разрезанного ребра
Вот несколько примеров связности графов:
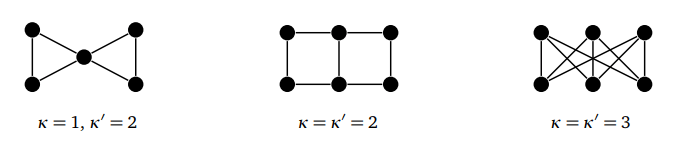
В примере выше delta — это обозначение минимальной степени в графе.
Доказательство теоремы
Докажем следующую теорему:
Для любого простого графа k≤ k * 0 ≤ delta
В этой теореме (k * 0) ≤ delta, потому что граф разомкнется, если удалить ребра, инцидентных вершине минимальной степени.
Покажем, что (k * 0) ≤ k:
- Пусть
E— минимальный набор ребер, удаление которых разбивает граф на две компоненты,SиT - Получается, что
|E| = (k * 0)
Может оказаться, что E состоит из всех ребер между S и T:
- Значит, у
Eесть множество ребер - При этом
|S|-|T|в сумме большеn-1 - При этом
n-1 ≥ k, гдеn— число вершин в графе - В противном случае существуют
s in Sиt in T, которые не смежные
Рассмотрим множество, которое состоит из всех соседей s в T и всех соседей t в S. Если удалить вершины этого множества, то это разъединит граф, так как мы не сможем попасть из s в t. Поэтому у этого множеств размер не менее k.
С другой стороны, ребра между двумя половинами этого множества исходят из E, поэтому его размер не больше κ 0. Значит, мы получаем (k * 0) ≤ k.
Наглядное доказательство этой теоремы:
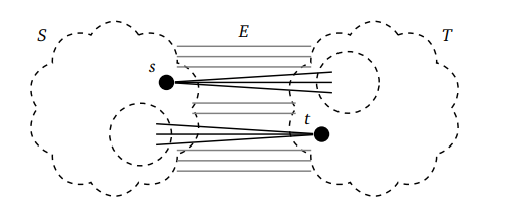
Также подграфы могут быть не просто связными, но и двухсвязными. Посмотрим, что получится из этого.
Блоки
Напомним, что компонента графа — это максимально связный подграф. Если мы заменим «связный» на «двухсвязный», то получим блок — это максимальный двухсвязный подграф графа.
Это подграф, который не содержит разрезанных вершин. Если добавить к нему любые другие вершины, из-за этого появится разрезанная вершина.
Мы можем разбить граф вокруг его разрезанных вершин на блоки:

Это несколько напоминает разбиение графа на компоненты. Только вместо того, чтобы разбивать граф на максимально связные части, мы разбиваем его на максимально двухсвязные части. Это важно, так как многие проблемы с графами можно упростить, если разбить граф на блоки.
Например, хроматическое число графа — это максимальное из хроматических чисел его блоков. В приведенном выше графе хроматическое число равно трем, так как для блока треугольника требуется три цвета, а для остальных — два.
В качестве других примеров можно привести число остовных деревьев в графе, равное произведению числа остовных деревьев в каждом блоке. Еще с блоками связаны планарные графы — такие, которые изобразить на плоскости без пересечений ребер не по вершинам. Планарность можно свести к блокам — граф планарен, когда все его блоки планарны.
Выводы
В этом уроке мы разобрались со связными подграфами, а также узнали, что произойдет, если связный заменить на двусвязный. В таком случае мы получим блок, у которого нет разрезанных вершин, но если добавить новые вершины, то тогда разрезанные появятся.
