Теория графов
Теория: Раскрашивание графа
В этом уроке мы разберем, что такое раскраска графов и как это относится к цифрам на вершинах. Также покажем примеры раскраски графов разных типов, так как в каждом случае этот процесс немного отличается.
Раскраска графов
Когда мы присваиваем вершинам графа метки — это называется раскраской графов.
Цвета — это целые положительные цифры. Графы нужно раскрашивать так, чтобы соседние вершины имели разные цвета. Еще стоит использовать как можно меньше цветов.
Вот несколько примеров раскраски графа:
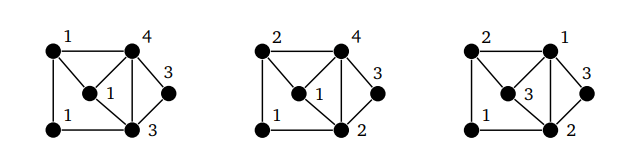
Первый пример на схеме выше не совсем верный, потому что соседним вершинам присваивается один и тот же цвет. Вторая раскраска лучше, так как удовлетворяет правилам, но в ней используется больше цветов, чем нужно. Третья раскраска — правильная. Она удовлетворяет правилам и использует как можно меньше цветов.
В этих графах невозможно использовать меньше трех цветов, так как треугольники содержат три вершины, которые являются соседями.
Хроматическое число графа G, которое обозначается chi(G) — это минимальное количество цветов, необходимое для правильной раскраски графа.
Чтобы обозначить, о каком графе идет речь, мы будем сокращенно обозначать chi(G) как chi. Рассмотрим раскраску графов на просто классе графов — путях.
Раскраска путей
Вот несколько оптимальных вариантов раскраски путей:

В общем случае chi(P_n) = 2 для каждого n ≥ 2.
Рассмотрим другие примеры:
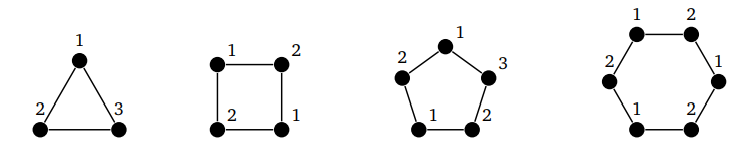
Четные и нечетные циклы ведут себя по-разному. У нечетных всегда хроматическое число три, а у четных — хроматическое число два.
Теперь рассмотрим, как раскрашивают полные графы.
Раскраска полных графов
У нас есть следующие полные графы с уже помеченными вершинами:

Поскольку в полном графе каждая вершина смежна с любой другой вершиной, мы не можем повторить ни одного цвета. Таким образом, chi(Kn ) = n.
Раскраска двудольных графов
Рассмотрим следующие примеры:

На графиках видно, что соседние вершины раскрашены в один цвет. В случае с двудольными графами такое возможно, так как применяется правило партитного множества — независимое множество, между вершинами которого нет ребер. Поэтому мы можем окрасить все его вершины в один цвет.
Для двух партитных множеств нужно два цвета. И это относится к любому двудольному графу, а не только к полному.
Любой граф с хотя бы одним ребром является двудольным, когда он двухцветный. Поскольку деревья двудольные, мы теперь знаем, что все нетривиальные деревья имеют хроматическое число 2.
Объединения и стыковки
Мы пришли к такой формуле:
chi(GcupH) = max(chi(G),chi(H))
Это связано с тем, что между копиями G и H в объединении нет ребер. Поэтому мы можем раскрасить каждый граф отдельно, и не беспокоиться:
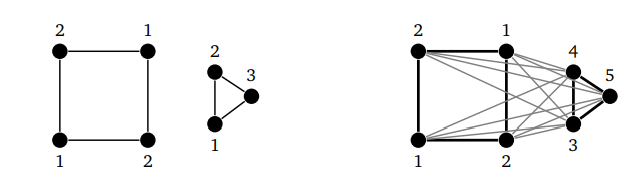
Мы также имеем chi(G vee H) = chi(G) + chi(H) — каждая вершина G смежна с каждой вершиной H. Поэтому ни один цвет, который используется на G, не может быть использован на H и наоборот.
Обратите внимание на второй граф на схеме выше. Чтобы получить правильную раскраску G vee H, мы можем раскрасить G и H отдельно, а затем заменить каждый цвет c из H на c + chi(G).
Декартово произведение
Декартово произведение немного сложнее. Результат chi(G H) = max(chi(G),chi(H)), что совпадает с результатом для объединения.
Рассмотрим пример: C5 C4. Ниже выделена конкретная вершина:
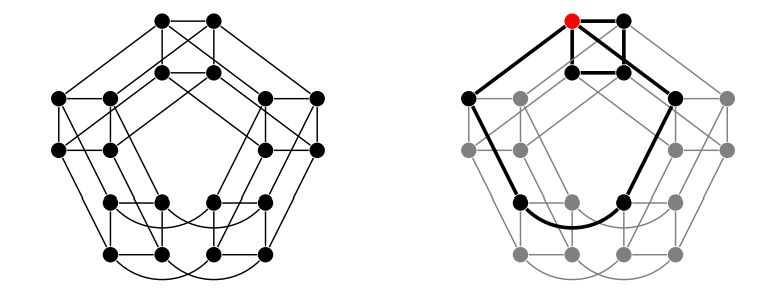
Выделенная вершина — это часть сразу двух графов (C5 и C4). Нам нужно убедиться, что ее раскраска работает в отношении обоих графов. Мы можем представить C5 и C4 как состоящий из пяти копий C4 со связями между копиями, которые определяются связями C5.
Нам нужно раскрасить каждую из пяти копий C4 по-своему и убедиться, что взаимодействия между копиями, которые определяются C5, соблюдены. Начнем с оптимальных раскрасок C4 и C5:

Хитрость в том, чтобы для каждой вершины взять ее цвет в C4, ее цвет в C5 и сложить их. При этом нужно уменьшить результат по модулю 3 и заменить все полученные нули тройками. В итоге раскраски для пяти копий выглядят следующим образом:
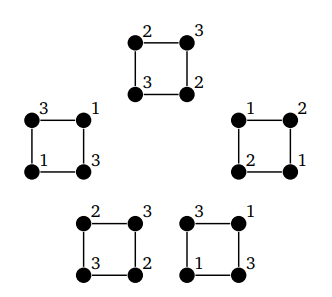
Такой способ гарантирует, что соседние вершины никогда не будут иметь одинаковый цвет. Этот же процесс работает и в общем случае:
- Для графов
GиHпусть будетm = max(chi(G),chi(H)) - Раскрасим вершину
(u, v)изGHцветом(cG(u)+cH (v)) mod m - Уточним, что в выражении выше
cG(u)иcH (v)— это цвета вGиHсоответственно
Произвольный граф
Вот еще один пример раскраски графа без очевидной структуры:
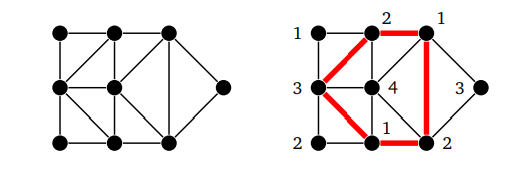
Может потребоваться некоторое усилие, чтобы придумать ответ к такой неочевидной структуре. Пройдем этот процес по шагам:
- На графе много треугольников, поэтому нам нужно использовать как минимум три цвета
- На графе справа выделен
5-цикл, для него требуется3цвета - Вершина в середине цикла смежна со всем циклом, поэтому мы не можем повторно использовать ни один из цветов цикла
- Таким образом, требуется
4цвета
Выводы
В этом уроке мы разобрали, что такое раскраска графов и как это относится к цифрам на вершинах. Мы показали, как раскрашивать графы разных типов. В каждом случае этот процесс немного отличается, при этом везде соблюдается правило соседних вершин.
