Функции
Теория: Онто-функции
Функция — это то, что связывает элементы или значения одного множества с элементами или значениями другого множества. Так элементы второго множества тождественно определяются элементами первого.
У функции много типов, которые определяют отношения между двумя множествами в различном виде. В этом уроке мы разберем один из типов — онто-функцию, которую также называют сюръективной. Также узнаем о ее определении, способе выяснения количества онто-функций и о том, как доказать, является ли функция сюръективной.
Что такое онто-функция
Онто-функция или сюръективная функция определяется с помощью двух множеств: A и B. Они состоят из элементов. Если для каждого элемента B существует хотя бы один или более одного элемента, который совпадает с A, то функция является онто-функцией:
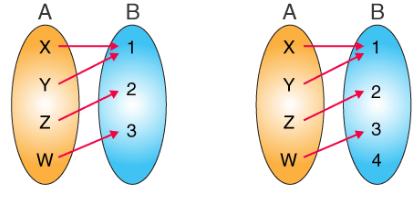
На первом рисунке видно, что для каждого элемента множества B существует пред-образ или совпадающий элемент в множестве A. Поэтому это онто-функция.
На втором рисунке один элемент множества B не сопоставлен ни с одним элементом множества A, поэтому это не онто-функция:
(1^m)(m-1)^n+(2^m)(m-2)^n-(3^m)(m-3)^n+...-((m-1)^m *1^n
Свойства онто-функции
Онто-функция обладает несколькими важными свойствами:
- Мы можем определить онто-функцию как функцию, которая выражает сюръекцию, если ограничивать ее кодомен своим диапазоном
- Область — это то, что может входить в функцию, кодомен — возможные исходы, а диапазон — фактический вход функции
Как определить количество онто-функций
Представим, что нам нужно найти число онто-функций от множества A с n количеством элементов. При этом функция относится к множеству B с m количеством элементов. В таком случае общее количество функций из A в B будет равно m^n. Вычисляется это так:
Общее количество онто-функций = Общее количество функций — Количество функций, которые не являются онто
Формула для нахождения общего числа функций, которые не являются онто, выглядит так:
m^n-(1^m)(m-1)^n+(2^m)(m-2)^n-(3^m)(m-3)^n+...-((m-1)^m *1^n)
В этой формуле:
- При
n > mчисло онто-функций= 0 - При
n = mчисло онто-функций= m!
Как работать с онто-функциями
Рассмотрим примеры онто-функции, чтобы лучше понять концепцию.
Определяем онто-функцию
Возьмем такое условие:
A = {1, 5, 8, 9}B = {2, 4}f = {(1, 2), (5, 4), (8, 2), (9, 4)}
Докажем, что f — онто-функция.
Посмотрим на условие еще раз и заметим, что все элементы на B имеют доменные элементы на A. Другими словами, у элементов 1, 8, 5 и 9 одинаковый диапазон — 2 и 4 соответственно.
Следовательно, f: A → B — это онто-функция.
Выясняем количество онто-функций
Возьмем другое условие:
- Множество
X = {1, 2, 3, 4} - Множество
Y = {a, b, c} n=4иm=3
Найдем количество онто-функций из множества X = {1, 2, 3, 4} в множество y= {a, b, c}.
Вспомним формулу, которую рассматривали выше:
m^n-(1^m)(m-1)^n+(2^m)(m-2)^n-(3^m)(m-3)^n+...-((m-1)^m *1^n)
Подставим значения m и n в формулу и получим:
= 34 - ^(3)C_(1)(2)^4 + ^(3)C_(2)(1)^4
= 81 - 3(16) + 3(1)
= 81 - 48 + 3 = 36
Таким образом, количество онто-функций из множества X в множество Y равно 36.
Выводы
В этом уроке мы узнали, что такое онто-функция. Так называют функцию, в которой есть два множества A и B в том случае, если для каждого элемента B существует хотя бы один или несколько элементов, совпадающих с множеством A. Любая функция называется онто-функцией, если в ней каждый элемент кодомена имеет один или несколько родственных элементов в домене. Онто-функция также известна как сюръективная функция.
