Поскольку функции — это отношения, у них есть графики. В этом уроке мы покажем, как визуально представить функцию.
График функции — это визуальное представление функции на плоскости, которое помогает понять различные свойства функции.
Графики функций можно строить по-разному, но процесс всегда похож — надо строить кривую, которая соответствует функции.
Вспомним типы графиков функций:
- Линейная
- Квадратичная
- Кубическая
- Рациональная
- Логарифмическая
Давайте выясним, как строить графики на примере линейной функции.
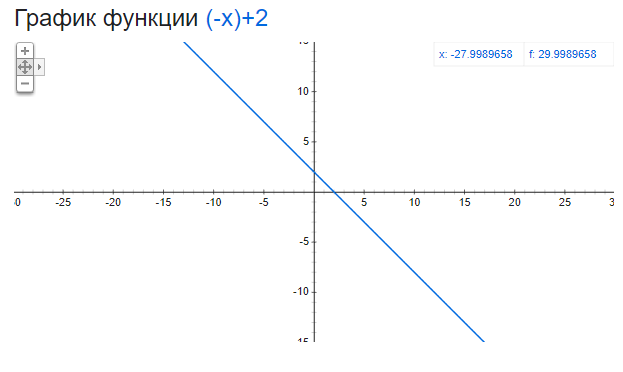
Шаг 1. Сначала построим график функции (f(x) = -x + 2). Для этого создадим таблицу значений, взяв несколько случайных чисел для x, скажем, x = 0 и x = 1. Затем подставим каждое из них в y = -x + 2, чтобы вычислить значения y:
x |
y |
|---|---|
0 |
-0 + 2 =2 |
1 |
-1 + 2 = 1 |
Таким образом, две точки на прямой — это (0, 2) и (1, 1). Если построить их на графике и соединить прямой линией, то мы получим ее график:
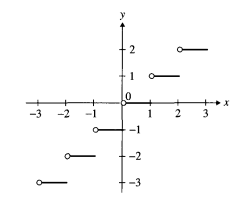
Посмотрим еще на такой пример — это часть графика функции Floor:
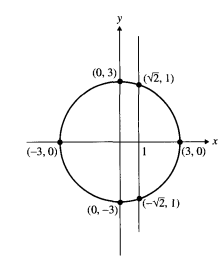
Представим, что G — график функции с областью X subset R x R.
В таком случае G будет являться графиком функции при одном условии: всякий раз, когда x_0 ∈ X, вертикальная прямая x = x_0 должна пересекаться G в одной точке. Это называется тестом вертикальной линии для функции.
Часто функции представляют в виде диаграммы. Например, когда у функции маленькое множество в качестве своей области и маленькое множество в качестве своего кодомена.
Допустим, есть такая функция:
F : {10, 1, 2} - {3, 5, 7}, определенная как F(0) = F(1) = 5 и F(2) = 7
Линии, которые соединяют элемент слева на рисунке с элементом справа — это связь между элементами области и элементами кодомена. Ее интерпретируют как правило для F. Например, мы интерпретируем линию между 0 и 5, как означающую F(0) = 5:
Теперь посмотрим на еще один пример:
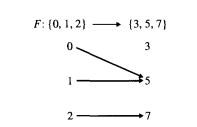
Элементы области и кодомена могут быть перечислены в любом порядке. Иногда подобное представление облегчает понимание функций, определенных на N — состоящих из натуральных чисел. Такое представление можно использовать и для некоторых больших множеств.
Выводы
В этом уроке мы вспомнили тему графиков и узнали, как работать с графиками функций. Эти знания пригодятся далее в курсе, когда мы будем изучать разные типы функций и их визуальные представления.
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
