Задача о супружеских парах — Комбинаторика

• Решаем задачу о супружеских парах
• Выводы

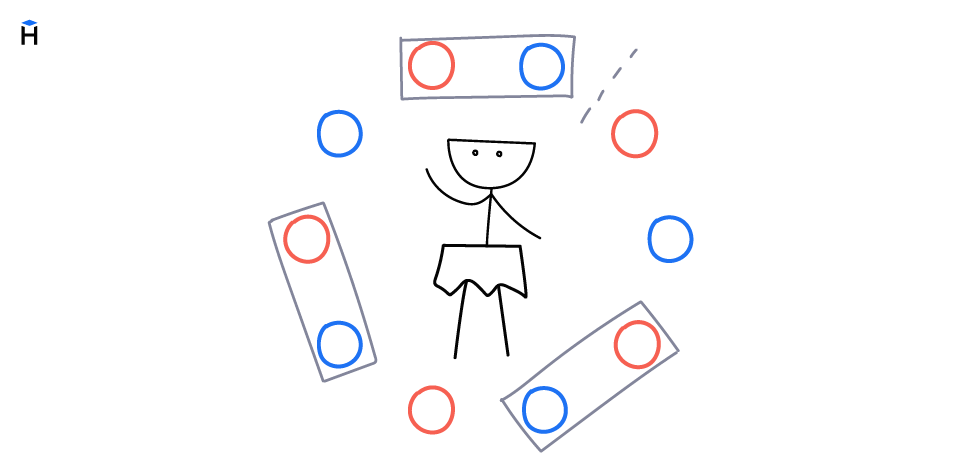
Представим, что вы организуете круглый стол, и вам важно, в каком порядке будут рассажены участники. В комбинаторике такую задачу называют «задачей о супружеских парах» или методом Le Problème des Ménages.

В этом уроке разберем, как работает такой метод.

Решаем задачу о супружеских парах

Для начала рассмотрим самую распространенную формулировку этой задачи:

Допустим, у нас есть n пар, каждая из которых состоит из мужчины и женщины.

Их нужно рассадить за круглым столом так, чтобы мужчины и женщины чередовались. При этом женщины должны сидеть на нечетных местах и ни одна из них не может сидеть рядом со своим партнером.

Нужно вычислить, сколько существует вариантов рассадки.

Чтобы решить эту задачу, используем принцип включения и исключения.

Для начала переведем задачу на язык математики и присвоим имена:

• Пусть 1, . . . , n — множество пар
• При этом A — множество рассадок, в которых женщины занимают нечетные места
• Нужно найти те члены в A, для которых ни одна пара не сидит вместе
• Выражение V subseteq n обозначим через множество расстановок AV
• Множество AV обозначает пары из множества V, которые нарушают правило
• По симметрии размер |AV | зависит от размера V, а не от конкретного выбора пар
• Поэтому сделаем такой вывод — если |V| = k, обозначим ak := |AV |

Далее находим нужное число. Для этого применим принцип включения и исключения:

sumnk=0(-1)k(nk)=0

Далее введем обозначение bk — это количество способов, с помощью которых можно выбрать k пар стульев, расположенных рядом друг с другом.

Наши k плохих пар могут располагаться над плохими парами мест k! способами. Поэтому мы приходим к такому выражению:

ak = b_kk!(n-k)!(n-k)!

После этого мы можем рассадить оставшихся женщин (n - k)! способами, а оставшихся мужчин — (n - k)! способами.

Вот так может выглядеть схема рассадки:

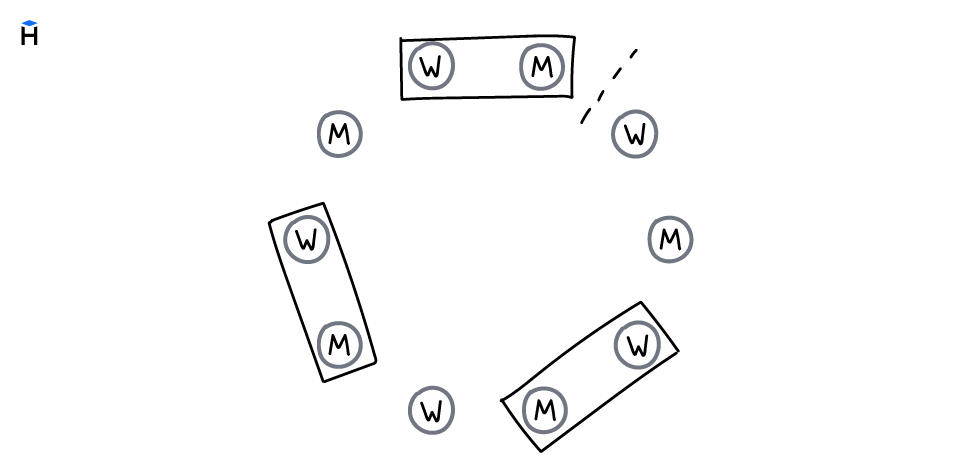
Здесь три пары сидят вместе, что не соответствует первоначальному условию рассадки.

Остается определить bk. Для этого разорвем окружность в фиксированной точке. Далее сотрем буквы в кругах, так как они фиксированы. Также стираем круги внутри прямоугольников, так как их количество известно — по два круга в каждом прямоугольнике.

В итоге получим такой рисунок:

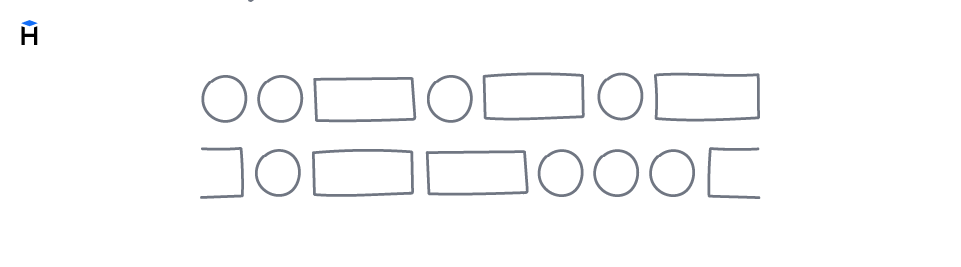
В процессе решения задачи мы пришли к такой формуле:

b^k=(2n-k)/k + (2n-k-1)/(k-1) = (2n-k)/k + k/(2n-k)times(2n-k)/k = 2n/(2n-k)times(2n-k)/k

Комбинируем приведенные формулы, немного упрощаем и получаем решение:

n!sum_{k=0}^{n}(2n)/(2n-k)times(2n-k)/ktimes(n-k)!(-1)^k

Выводы

Теперь вы знаете, как решать задачи типа «супружеских пар». С помощью этого метода можно вычислить количество вариантов расположения элементов по условиям, которые мы задали.

Особенность такого метода заключается в том, что для решения можно использовать принцип включения и исключения, который мы изучили ранее.

---

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты