Комбинаторика
Теория: Теория графов

В этом курсе мы изучили базовые темы комбинаторики — области математики, занимающаяся проблемами выбора, расположения и работы в конечной или дискретной системе. Но пока мы не затрагивали один важный аспект этой темы — комбинаторную геометрию. В этом уроке мы обсудим, как комбинаторика связана с геометрией и какие темы стоит изучать дальше.
Как углубить знания в комбинаторике
Одной из основных задач комбинаторики — определить число возможных конфигураций заданного типа. Даже если конфигурация задается простыми правилами, перечисление иногда может представлять огромные трудности. В таких случаях математик довольствуется приблизительным ответом или диапазоном с нижней и верхней границей. Это одна из сложностей, которая есть в комбинаторике.
В математике обычно говорят о «существовании». Сущность существует, если математический пример удовлетворяет абстрактным свойствам, определяющим сущность. Неочевидно, что существует даже единственная конфигурация с определенными заданными свойствами. Такая ситуация порождает проблемы существования и конструирования. Эти абстрактные формулировки используются и в комбинаторных задачах, и в этом состоит вторая сложность.
Считается, что комбинаторика нужна только для счета, но на деле она шире. Она решает и неожиданные вопросы, например, «Возможна ли определенная комбинация?». Но чтобы отвечать на такие вопросы с помощью комбинаторики, нужно добавить в нее конкретики. В этом помогает теория графов.
Что такое теория графов
Теория графов занимается графами — различными типами сетей или моделями сетей. Сами графы выглядят как точки, соединенные линиями:
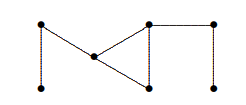
Вместо точек и линий в теории графов используются другие термины — вершины и ребра. Рассмотрим несколько примеров графов, чтобы лучше понять, о чем речь.
Задача с домино и шахматной доской
Предположим, у нас есть шахматная доска и набор домино, в котором каждая костяшка занимает два квадрата на шахматной доске. Можно ли покрыть всю доску этими костяшками? Сначала уточним правила:
- Доска покрыта, если костяшки уложены так, что каждая из них покрывает ровно два квадрата доски
- Ни одна костяшка не пересекается с другой
- Каждая клетка доски в итоге покрыта
Ответ на эту задачу прост: чтобы покрыть доску, надо выложить 32 костяшки в ряд. Чтобы сделать задачу более интересной, добавим два новых условия:
- Доска может быть прямоугольником любого размера
- Можно убрать с доски некоторые квадраты
Доска может быть примерно такой:
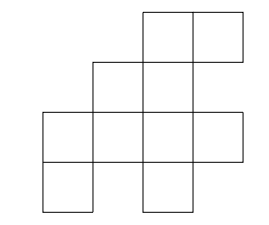
Можно ли ее покрыть целиком? Вот простое наблюдение: каждая костяшка должна покрывать две клетки, поэтому общее количество клеток должно быть четным; при этом доска имеет четное количество клеток. Достаточно ли этого? Нетрудно убедить себя, что эта доска не может быть покрыта, но все не так просто. Предположим, мы перерисуем доску, чтобы подчеркнуть, что это действительно часть шахматной доски:
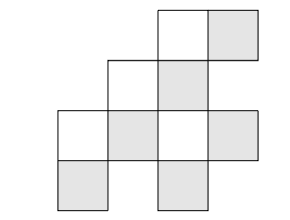
Теперь мы узнали кое-что новое — у нас есть четыре белых и шесть серых плиток. Каждая плитка должна покрывать один белый и один серый квадрат, но это невозможно. Теперь у нас есть полная картина? Снова неочевидно:
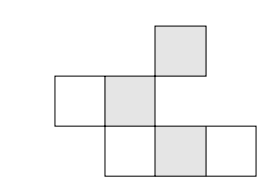
Серый квадрат в правом верхнем углу явно не может быть покрыт, потому что у него нет пары.
К сожалению, нелегко сформулировать условие, чтобы оно полностью характеризовало доски, которые можно покрыть — мы еще встретимся с этой проблемой. Отметим, что эту задачу можно представить в виде графа. Введем вершину, соответствующую каждому квадрату. Затем соединим две вершины ребром, если связанные с ними квадраты могут быть покрыты одним домино. Вот предыдущая доска в виде графа:
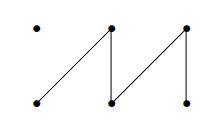
Расшифруем, что здесь обозначено:
- Верхний ряд вершин — серые квадраты
- Нижний ряд вершин — белые квадраты
- Ребра — костяшки домино
Теперь мы можем размышлять так: «Костяшки соответствует набору ребер, которые не имеют общих конечных точек и касаются всех шести вершин. Ни одно ребро не касается левой верхней вершины, поэтому эта клетка на шахматной доске не закроется».
Задача с раскраской
Возможно, самая известная задача в теории графов связана с раскраской карт. Она сформулирована так: «Если дана карта некоторых стран, то сколько цветов необходимо, чтобы раскрасить карту так, чтобы страны с общей границей имели разные цвета? Долгое время предполагалось, что любую карту можно раскрасить четырьмя цветами, и это было окончательно доказано в только 1976 году. Вот пример небольшой карты, раскрашенной четырьмя цветами:
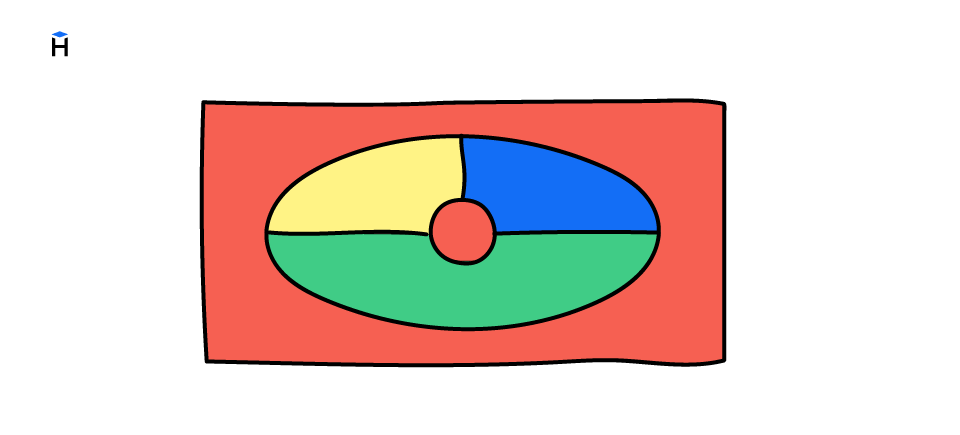
Обычно эту проблему превращают в задачу теории графов. Предположим, что мы добавим к каждой стране столицу и соединим столицы через общие границы. Раскрашивание столиц так, чтобы ни одна из двух соединенных столиц не имела общего цвета — это та же проблема. Для предыдущей карты схема со столицами будет выглядеть так:
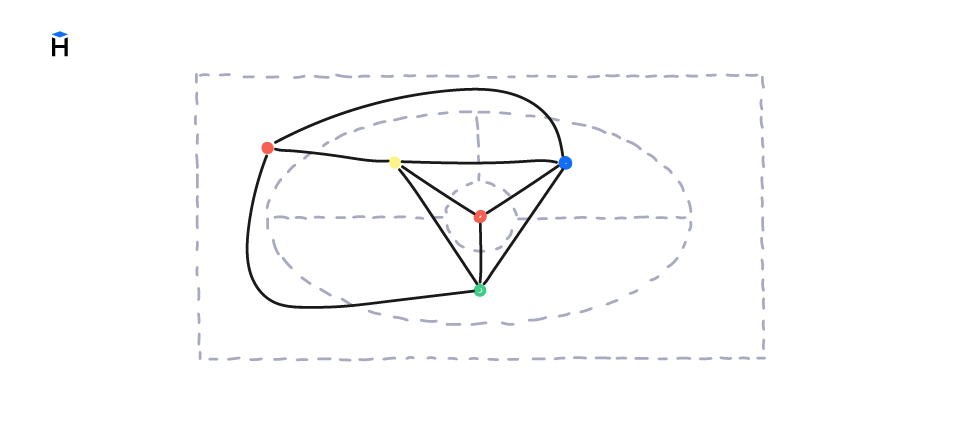
Выводы
В этом уроке мы узнали об еще одной области математики, которая помогает глубже погрузиться в комбинаторику — это теория графов. Вы познакомились с понятием графа и рассмотрели его на известных примерах. Эти знания пригодятся в других наших курсах по математике.
