Представьте, что ребенок держит в руках несколько красных и желтых кубиков. Он выставляет их в ряд, потом перемешивает и выставляет в новый ряд. Таких комбинаций может быть много — число будет зависеть от количества кубиков каждого цвета.
Мы можем узнать, сколькими способами можно расположить в ряд кубики красного и желтого цветов — для этого используется метод производящих функций. В этом уроке разберем, что такое производящая функция, рассмотрим ее обычный вид и научимся ее использовать.
Что такое производящая функция
Производящая функция — это многочлен, коэффициенты которого соответствуют членам последовательности чисел a_n. Эту функцию используют, чтобы решать реккурентные соотношения, потому что она умеет кодировать информацию о целочисленной последовательности.
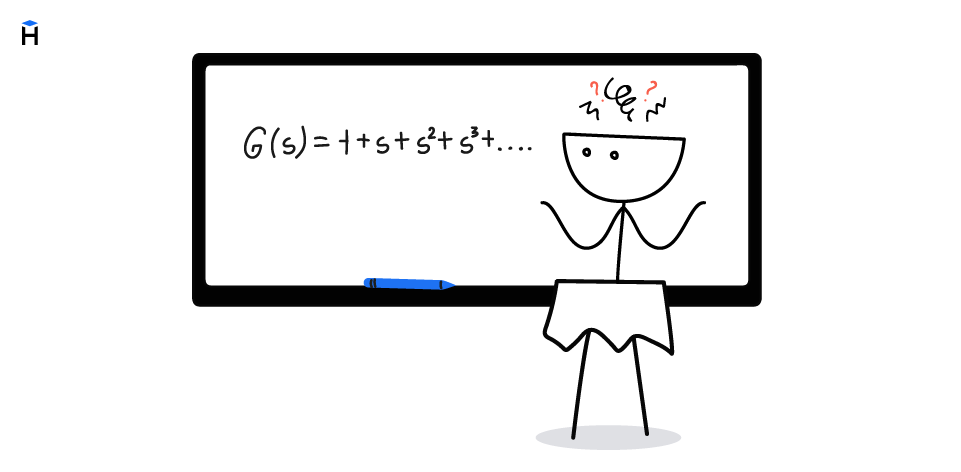
Например, простая последовательность — это постоянная последовательность 1, 1, 1, . . ..
Производящая функция для нее:
G(s) = 1 + s + s^2 + s^3 + . . .
Когда функция используется без уточнения, ее называют обычной производящей функцией. Разберем подробнее, как она выглядит.
Как выглядит производящая функция
Обычная производящая функция — это функция вида f(x) = n=0suminftyanxn. Разберем на примере, как ее использовать.
Представим, что нам нужно найти, сколькими способами можно составить сумму 10. При этом можно использовать по одному элементу из каждого из следующих двух наборов: {2,3,6,7} и {3,4,5,8}.
Рассмотрим два многочлена:
x^2 + x^3 + x^6 + x^7x^3 + x^4 + x^5 + x^8
x^n — это количество способов составить сумму n с помощью одного элемента из каждого набора.
Например, коэффициент x^4 во втором многочлене равен 1. Значит, существует один способ составить сумму из четырех, используя только один элемент из набора.
Теперь рассмотрим произведение многочленов:
(x^2 +x ^ 3 +x ^ 6 +x ^ 7 )(x ^ 3 +x ^ 4 +x ^ 5 +x ^ 8 )
В полиномиальном произведении x^n — количество способов составить сумму из n, когда берется по одному числу из каждого набора.
Разложим произведение:
(x^2 + x^3 + x^6 + x^7)(x^3 + x^4 + x^5 + x^8) = x^5 + 2x^6 + 2x^7 + x^8 + x^9 + 3x^10 + 3x^11 + x^12 + x^14 + x^15
Коэффициент x^n равен нулю при n > 15, так как мы не можем получить сумму больше 15. Если взять самые большие числа из каждого набора, то получится число 15 - 7 + 8.
То же самое относится и к (n > 5). Берем самые маленькие числа из наборов и получаем (5 - 2 + 3).
Когда n = 10, коэффициент равен трем. Это означает, что есть три способа получить число 10. Если c помощью формулы дистрибутивности мы развернем произведение полностью, то увидим, что три члена x^{10} получаются из произведений:
x^2 * x^8x^6 * x^4x^7 * x^3
Производящая функция придает смысл коэффициенту x^n, но не придает смысла x. Она кодирует числа объектов с помощью формальных степенных рядов — многочленов с бесконечно большим количеством членов.
В разобранном примере можно было просто подсчитать количество способов получения числа 10 путем проверки. Но производящие функции полезны, когда многочлены выражены в более компактной форме — например, с помощью суммы геометрического ряда.
Выводы
В этом уроке мы изучили метод производящих функций, рассмотрели ее обычный вид и научились ее использовать. Теперь в вашем арсенале есть еще один инструмент для решения задач в комбинаторике.
Самостоятельная работа
Задача №1
У Васи есть четыре вида лука в разном количестве:
- Пурпурный — количество может быть любым неотрицательным целым числом
- Зеленый — количество кратно 2
- Красный — количество кратно 3
- Синий — количество кратно 4
Если у Васи 23 луковицы, сколько различных распределений цветов может быть?
Нажмите, чтобы увидеть ответ
Мы хотим найти количество неотрицательных целочисленных решений задачи. Сначала обозначим цвета буквами: * Пурпурный — `a` * Зеленый — `b` * Красный — `c` * Синий — `d` Далее обозначим общее количестов луковиц через формулу: `a + b + c + d = 23` Таким образом, мы можем обозначить формулами луковицы всех цветов: * `a=k`, где `0≤k≤23` * `b=2k`, где `0≤k≤11` * `c=3k`, где `0≤k≤7` * `d=5k`, где `0≤k≤4` * `(\sum_{k=0}^{23} x^k )(\sum_{k=0}^{11} x^{2k} )(\sum_{k=0}^7 x^{3k})(\sum_{k=0}^4 x^{5k})` По формулам выше мы видим, что коэффициент `x^{23}` в разложении равен **`127`**. Другой способ заключается в решении задачи по `d`, через синий цвет. **Случай `1: d=20`:** Мы видим, что `(0, 0, 3, 20)` подхоит: `0+0+3+20=23`. `(1, 2, 0, 20)` и `(3, 0, 0, 20)` также подхоят. Получаем `3` вартанта. **Случай `2: d=15`** `(0, 2, 6)` и `(2, 0, 6): 2` варианта в этом подслучае, при `c=6`. `(1, 4, 3), (3, 2, 3), (5, 0, 3): 3` в этом подслучае. `(0, 8, 0) ... (8, 0, 0): 5` в этом подслучае. Итого в этом случае `10` вариантов. **Случай `3: d=10`** `c=12: 1` здесь `c=9: 3` здесь `c=6: 4` здесь `c=3: 6` здесь `c=0: 7` здесь На этом этапе вы должны увидеть закономерность: мы можем доказать это, взяв два случая: один, где `c` нечетное, и другой, где `c` четное. Всего здесь `21` случай. **Случай `4: d=5`** `c=18: 1` здесь `c=15: 2` здесь Отсюда мы можем получить, что сумма для этого случая равна `1+2+4+5+7+8+10=37`, по аналогии со случаем `3`. **Случай `5: d=0`** `c=21: 2` здесь `c=18: 3` здесь `2+3+5+6+8+9+11+12=56` в этом случае. Суммируя все это, получаем `3+10+21+37+56=127`Задача №2
Найдите количество неотрицательных целочисленных решений задачи 3x+y+z=24.
Нажмите, чтобы увидеть ответ
В условии есть такие данные: * `3x+y+z=24` * `x≥0` * `y≥0` * `z≥0` Пусть: * `x=k` * `thereforey+z=24-3k...(i)` * `24≥24-3k≥0(becausex≥0)` Следовательно: * `0≤k≤8` Далее вычисляем `i` — общее число интегральных решений: `(24-3k+2-1)_C_(2-1)=(25-3k)_C_1=25-3k` Отсюда следует, что общее количество решений исходного уравнения равно 117: `((k=0)sum(8))(25-3k)=25((k=0)sum(8))(1)-3((k=0)sum(8))(k)`\ `=25.9-3*(8.9/2)=225-108=117`Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
