Как и в любом другом разделе математики, в комбинаторике есть свои элементарные инструменты — они помогают решать задачи и упрощать сложные выражения. В этом уроке мы изучим два базовых инструмента — принцип голубятни и двойной счет.
Принцип голубятни
Принцип голубятни или принцип Дирихле — это комбинаторное правило, которое можно сформулировать так:
Возьмем n коробок и разложим по ним m предметов. По крайней мере один из ящиков должен содержать более одного предмета при условии, что m > n
Свое название правило получило от знаменитого примера с голубями. Его привел математик Петер Дирихле:
Если построить голубятню на n мест и поселить в нее (n + 1) голубей, то как минимум одно место будет занято несколькими голубями
Согласно этому принципу, если n объектов (голубей) разместить в m коробок, то хотя бы одна коробка будет содержать n/m объектов. Так это выглядит на примере с голубями:
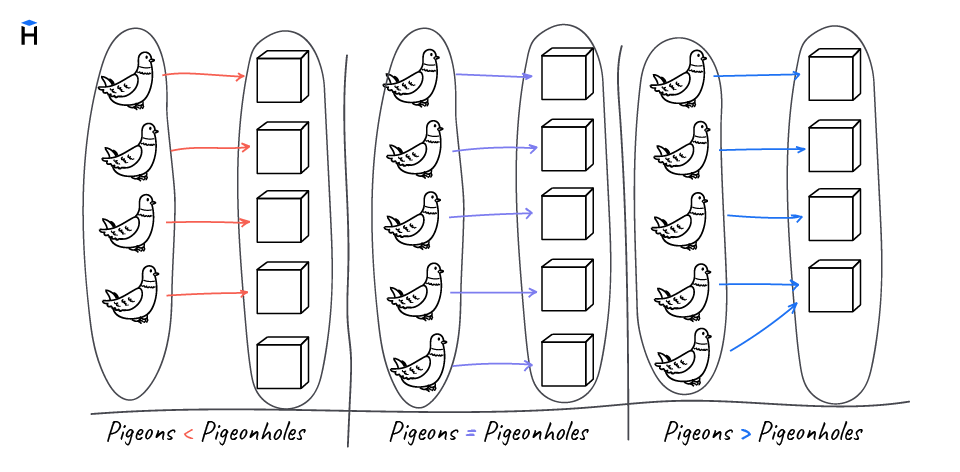
Этот же принцип можно использовать в другом интересном примере:
В толпе из 367 человек найдется как минимум два человека с одинаковым днем рождения
Чтобы доказать эту мысль, применим принцип голубятни. В примере выше есть 367 человек и только 366 возможных дней в году (с учетом високосного года). Дней меньше, чем людей — то есть не всем людям достанется уникальный день рождения. Поэтому по крайней мере два человека будут с одинаковым днем рождения.
Возьмем похожий пример. Представим колледж, в котором нужно провести 679 уроков за 35 доступных слотов в расписании. Как выяснить минимальное количество кабинетов для этой задачи? Нужно разделить 679 уроков на 35 доступных слотов — получится 19.4. Округлим до 20 кабинетов, чтобы не столкнуться с ситуацией, когда приходится проводить два урока в одном кабинете.
В курсе мы разберем еще множество задач и увидим, как принцип голубятни помогает в решении простых задач и заметно упрощает работу над сложными.
Элементарные инструменты: двойной счет
«Двойной счет» или «счет двумя способами» — это комбинаторная техника, с помощью которой можно доказать равенство двух выражений. Само правило можно сформулировать так:
Два выражения равны, если они являются двумя способами подсчета размера одного и того же множества
Другими словами, если два выражения решают одну и ту же задачу, значит они равны между собой. Это правило часто используют для доказательства комбинаторных тождеств:
Разберем на примере:
Представим, что мы проводим экзамен и раздаем 7 студентам бланки с 9 заданиями. Каждый студент должен выполнить не менее 4 заданий. Как доказать, что есть хотя бы одно задание, которое выполнили не менее 4 учеников?
Для начала определим недостающие значения:
7*4=28 заданий, которые студенты должны сделать (минимальное значение)\
7*9=63 задания, которые студенты могут сделать вообще (максимальное значение)
Чтобы решить задание, применим двойной счет.
Первый способ: Подсчитаем общее количество заданий, выполненных каждым из 7 студентов. Количество выполненных заданий обозначим через x:
28 ≤ x_1 + ... + x_7 ≤ 63
Второй способ: Подсчитаем, сколько студентов решили задачу номер 1, 2 и так далее. Если y_j — это количество студентов, решивших j - e задание, то общее количество выполненных заданий обозначается так:
y_1 + y_2 + ... + y_9 = x_1 + ... + x_7
Из этого равенства делаем вывод:
28≤y_1 + y_2 + ... + y_9 ≤ 63
Нижняя граница достижима, только если хотя бы одно из y_j больше или равно 4 (потому что 9 * 3 = 27 > 28). То есть студенты сдадут экзамен только в том случае, если в бланке есть задания, на которые ответят не менее 4 студентов. На этом доказательство завершено.
Выводы
В этом уроке мы познакомились с двумя базовыми инструментами комбинаторики:
- Принцип голубятни — если взять
nкоробок и положить в нихm > nпредметов, то по крайней мере один из ящиков должен содержать более одного предмета - Двойной счет — два выражения равны, если они являются двумя способами подсчета размера одного и того же множества
Эти принципы помогут вам решать простые комбинаторные задачи и упрощать решения в более сложных случаях.
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
