Алгоритмы на деревьях

Теория: KD-деревья

Полный доступ к материалам

Зарегистрируйтесь и получите доступ к этому и десяткам других курсов

Одна из самых популярных практических задач в современном программировании — это поиск ближайших соседей. Например, поиск ближайших соседей встречается в медицине. Так строятся прогнозные модели заболеваемости, в которых оцениваются контакты в ближайшем окружении заболевшего:

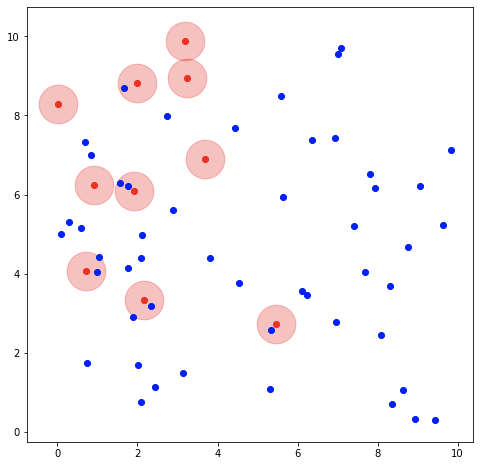
На рисунке выше вы можете увидеть координатную плоскость, на которой расположены:

«Заболевшие» красные точки
«Здоровые» синие точки
«Опасные зоны» — розовые окружности вокруг красных точек

Синяя точка подвергается риску заболеть, если она входит в опасную зону — располагается слишком близко к красной точке. Другими словами, чтобы синяя точка не заболела, расстояние между ней и красной точкой должно быть выше порогового значения.

В этом примере задача сводится к поиску синих точек с высоким риском заболеть. Один из способов решения такой задачи — это кластеризация на основе методов машинного обучения. Но есть и альтернатива — это KD-деревья, о которых мы и поговорим в этом уроке.

Что такое KD-деревья

KD-деревья — это дерево, вершины которого представлены в форме точек в некоторой K-мерной системе координат. Еще их называют K-dimensional trees или «K-мерные деревья».

В этом курсе мы рассматриваем только KD-деревья в двумерном пространстве. Но с его помощью можно вычислять ближайшего соседа и на более сложных системах координат. Например, так выглядит трехмерное дерево:

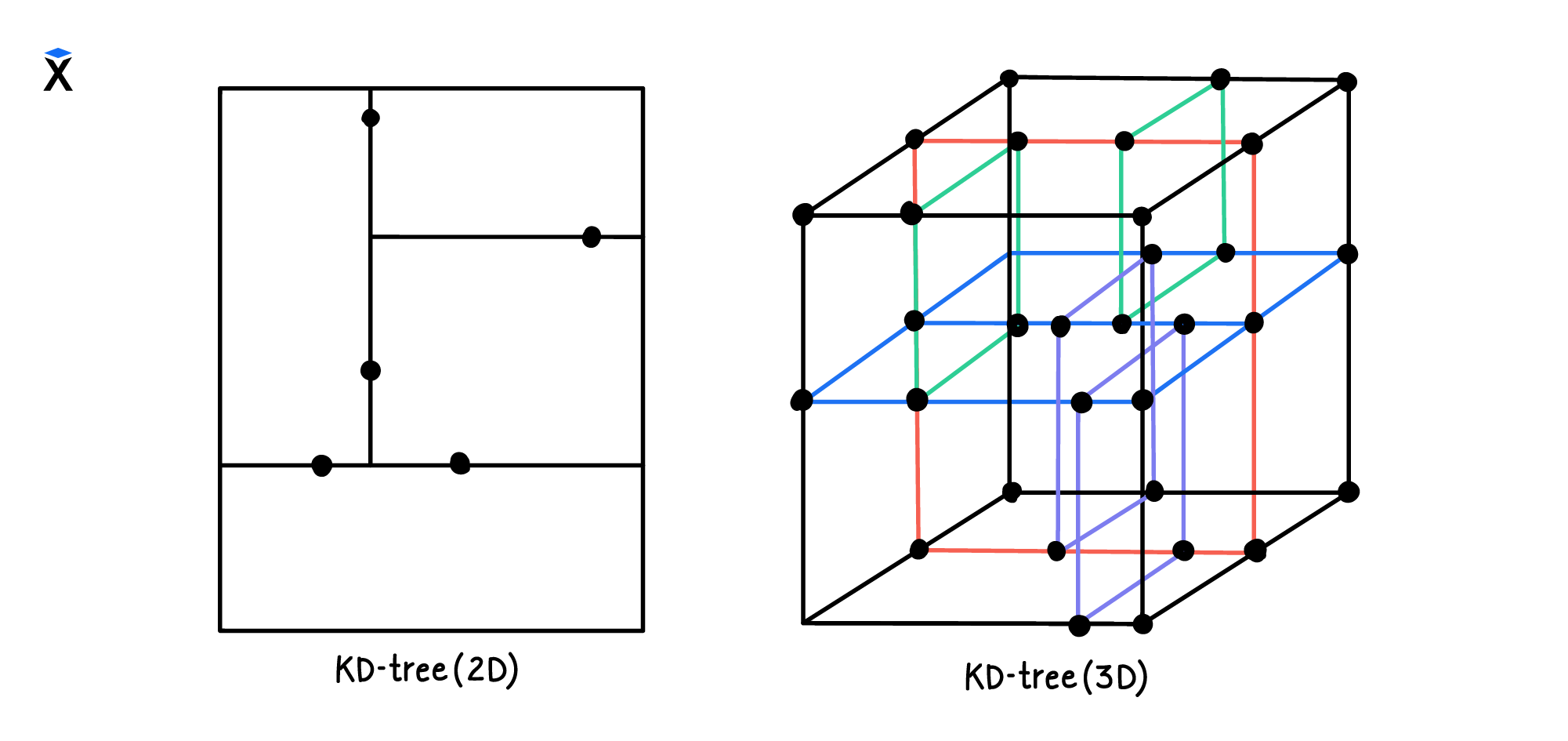
Обратим внимание, что эффективность поиска ближайших соседей в KD-дереве снижается при больших значениях K.

В качестве правила обычно принимают, что число вершин в дереве должно быть намного больше значения 2^K. Если это правило не соблюдать, то алгоритм поиска на основе KD-дерева будет работать с почти той же скоростью, что и обычный последовательный поиск.

Как устроено KD-дерево

Чтобы изучить строение KD-дерева, возьмем для примера 13 точек в двумерной системе координат:

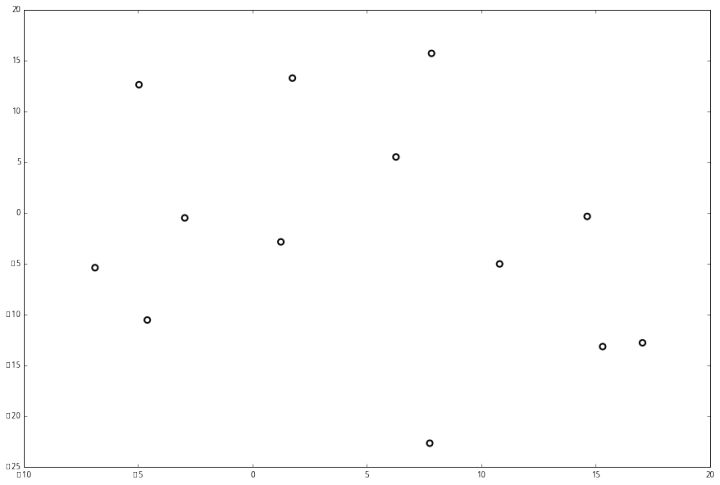
Чтобы построить по ним дерево, мы будем руководствоваться следующим алгоритмом:

Выберем ось в наборе данных
Найдем на этой оси медианное значение числа точек. Для двумерного пространства это значит, что справа и слева от значения должно быть одинаковое число точек. Если у нас четное число точек, то можно левое подпространство сделать больше правого
Проведем линию, которая разделит пространство на две части
Изменим ось и нарисуем свою медиану для каждого нового подпространства

Пройдя эти четыре шага, мы выполним первое разделение дерева. Далее мы повторяем все шаги до тех пор, пока точек больше не останется.

Посмотрим, как разделение работает на нашем примере — двумерном KD-дереве с 13 точками:

Этап 1. Разделим пространство на основании оси X:

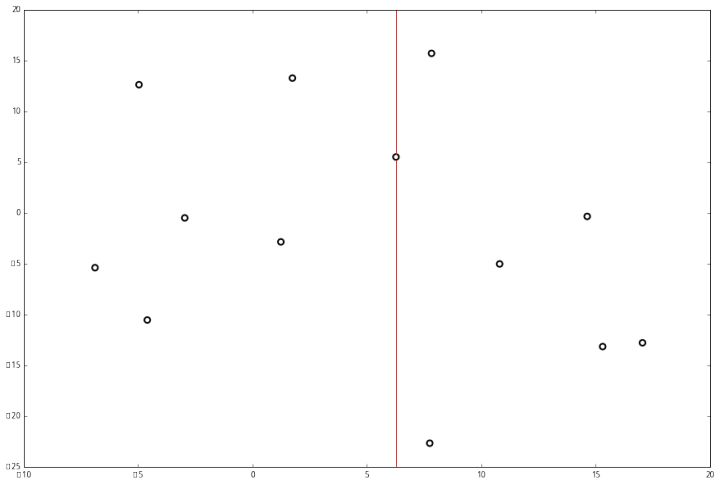
Этап 2. Выполним второе разделение на основании оси Y:

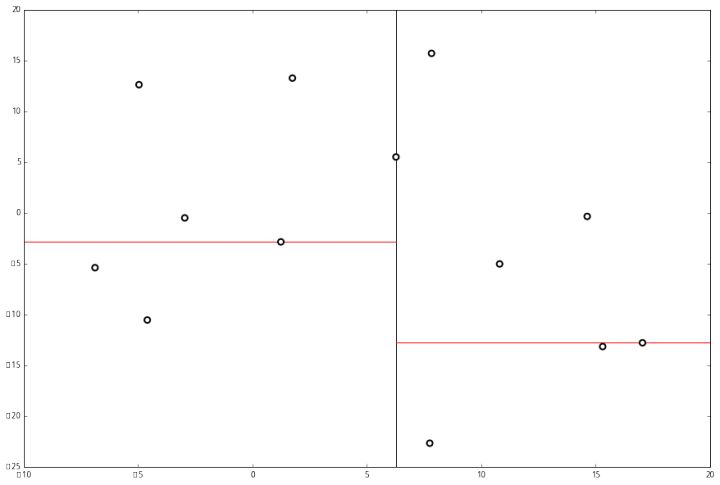
Этап 3. Продолжаем разделение, пока это возможно:

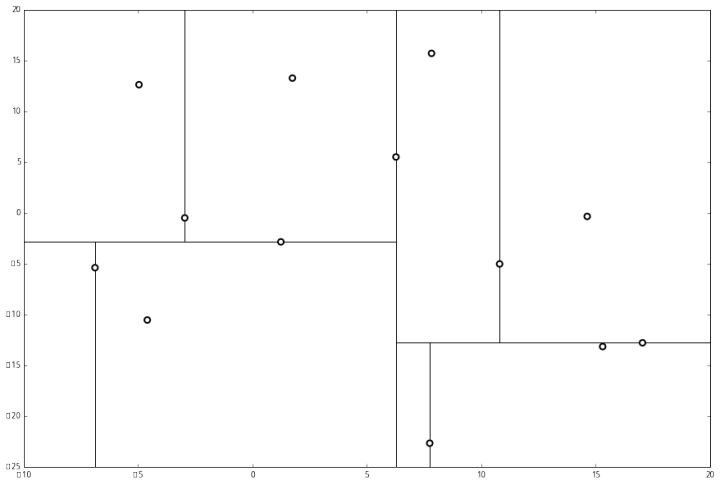
Этап 4. Строим итоговое дерево, исходя из разделения пространства:

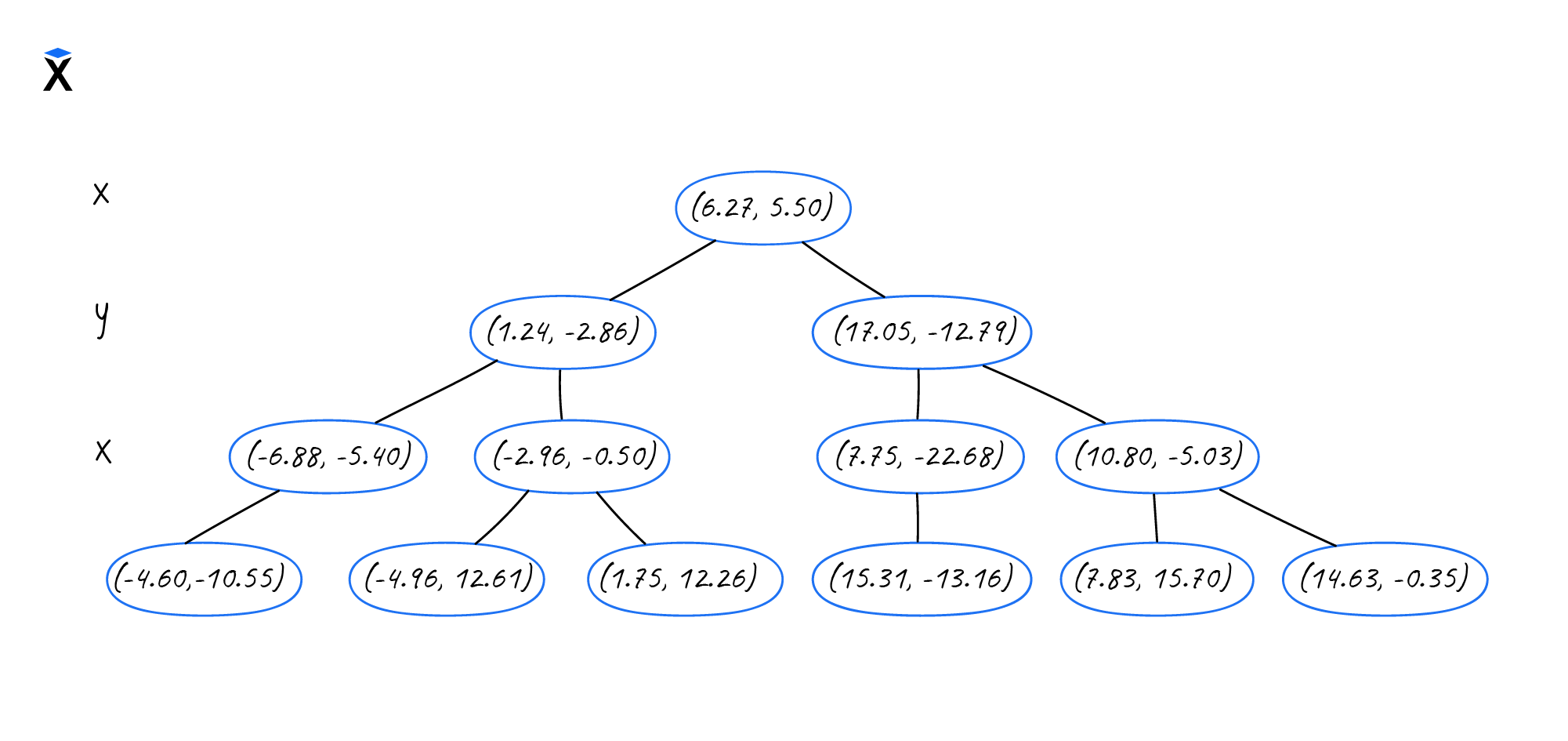
На последнем рисунке видно, что получившееся дерево аналогично сбалансированному бинарному дереву. Разница только в том, что в качестве полезной нагрузки в KD-дереве хранится точка с координатами.

В таком случае JavaScript-код узла будет выглядеть так:

class KDTreeNode {
  constructor(obj, dimension, parent) {
    this.obj = obj
    this.dimension = dimension
    this.right = null
    this.left = null
    this.parent = parent
  }
}

Операции над KD-деревом

Основное отличие KD-дерева можно увидеть при работе с методом, который отвечает за построение дерева из массива точек:

class KDTreeNode {
  // ...

  static buildTree(points, depth, dimensions, parent) {
    let dim = depth % dimensions.length
    let median, node

    if (points.length === 0) {
      return null
    }
    if (points.length === 1) {
      return new KDTreeNode(points[0], dim, parent)
    }

    points.sort(function (a, b) {
      return a[dimensions[dim]] - b[dimensions[dim]]
    })

    median = Math.floor(points.length / 2)
    node = new KDTreeNode(points[median], dim, parent)

    node.left = KDTreeNode.buildTree(points.slice(0, median), depth + 1, dimensions, node)
    node.right = KDTreeNode.buildTree(points.slice(median + 1), depth + 1, dimensions, node)

    return node
  }
}

Вызвать построение дерева можно при помощи следующего примера:

const points = [
  { x: 1, y: 2 },
  { x: 3, y: 4 },
  { x: 5, y: 6 },
  { x: 7, y: 8 },
]

const tree = KDTreeNode.buildTree(points, 0, ['x', 'y'], null)

Структура KD-дерева не отличается от бинарного дерева. Поэтому методы удаления и вставки узлов работают так же, как в бинарном дереве:

class KDTreeNode {
  // ...

  insertNode(value) {
    this.insertNodeHelper(value, this)
  }

  insertNodeHelper(value, parentNode) {
    if (value[this.dimension] < parentNode.obj[parentNode.dimension]) {
      if (parentNode.left === null) {
        parentNode.left = new KDTreeNode(
          value,
          this.dimension,
          parentNode,
        )
      }
      else {
        this.insertNodeHelper(value, parentNode.left)
      }
    }
    if (value[this.dimension] >= parentNode.obj[parentNode.dimension]) {
      if (parentNode.right === null) {
        parentNode.right = new KDTreeNode(
          value,
          this.dimension,
          parentNode,
        )
      }
      else {
        this.insertNodeHelper(value, parentNode.right)
      }
    }
  }
}

Удаление:

class KDTreeNode {
  // ...

  removeNode(value) {
    this.#removeNodeHelper(value, this)
  }

  #removeNodeHelper(value, node) {
    if (node === null) {
      return null // Узел не найден, возвращаем null
    }

    if (value[this.dimension] < node.obj[node.dimension]) {
      node.left = this.removeNodeHelper(value, node.left)
    }
    else if (value[this.dimension] > node.obj[node.dimension]) {
      node.right = this.removeNodeHelper(value, node.right)
    }
    else {
      // Узел найден
      if (node.left === null) {
        return node.right // Узел имеет только правого потомка
      }
      else if (node.right === null) {
        return node.left // Узел имеет только левого потомка
      }

      // Узел имеет обоих потомков
      let original = node
      node = node.right
      while (node.left) {
        node = node.left
      }

      node.right = this.#removeMin(original.right)
      node.left = original.left
    }
    return node
  }

  #removeMin(node) {
    if (node.left === null) {
      return node.right // Если нет левого потомка, возвращаем правого потомка
    }
    node.left = this.removeMin(node.left) // Рекурсивно вызываем removeMin для левого потомка
    return node
  }
}

Еще одной отличительной особенностью KD-дерева считается реализация метода поиска ближайшего соседа:

class KDTreeNode {
  // ...

  metric(point1, point2) {
    return Math.sqrt(
      Math.pow(point1.x - point2.x, 2) + Math.pow(point1.y - point2.y, 2),
    )
  }

  nearestSearch(point, node, bestNodes, maxNodes) {
    if (node === null) {
      return // Достигнут конец дерева
    }

    let dimension = this.dimension
    // Хранит расстояние между искомой точкой и текущим узлом дерева.
    let ownDistance = this.metric(point, node.obj)
    // для хранения координат точки, которую сравниваем с узлом.
    let linearPoint = {}
    // Расстояние между linearPoint и объектом текущего узла. Помогает решить, стоит ли искать в другом поддереве.
    let linearDistance
    // Ссылки на дочерние узлы. bestChild — поддерево с вероятным ближайшим соседом, otherChild — другое поддерево для проверки.
    let bestChild, otherChild

    for (let i = 0; i < this.dimension.length; i++) {
      if (i === this.dimension) {
        linearPoint[this.dimension[i]] = point[this.dimension[i]]
      }
      else {
        linearPoint[this.dimension[i]] = node.obj[this.dimension[i]]
      }
    }

    linearDistance = this.metric(linearPoint, node.obj)

    if (
      bestNodes.length < maxNodes
      || ownDistance < bestNodes[bestNodes.length - 1][1]
    ) {
      if (bestNodes.length === maxNodes) {
        bestNodes.pop() // Удаляем последний элемент, если массив лучших узлов уже заполнен
      }
      bestNodes.push([node.obj, ownDistance]) // Добавляем текущий узел в массив лучших узлов
      bestNodes.sort((a, b) => a[1] - b[1]) // Сортируем массив лучших узлов по расстоянию
    }

    if (
      bestNodes.length < maxNodes
      || Math.abs(linearDistance) < bestNodes[bestNodes.length - 1][1]
    ) {
      if (linearDistance < 0) {
        bestChild = node.right
        otherChild = node.left
      }
      else {
        bestChild = node.left
        otherChild = node.right
      }
      this.nearestSearch(point, bestChild, bestNodes, maxNodes) // Рекурсивно ищем в ближайшем поддереве
      if (Math.abs(linearDistance) < bestNodes[bestNodes.length - 1][1]) {
        this.nearestSearch(point, otherChild, bestNodes, maxNodes) // Поиск в другом поддереве, если необходимо
      }
    }
  }
}

Для определения расстояния между точками используется метрика, чаще всего евклидова. Она позволяет вычислить, насколько близко одна точка находится к другой, что является ключевым аспектом при поиске ближайших соседей.

Процесс поиска ближайших соседей

Инициализация:
- Поиск начинается с корневого узла дерева и заданной точки, для которой необходимо найти ближайшие соседи.
Рекурсивный поиск:
- На каждом уровне дерева происходит сравнение координат искомой точки с координатами узла. В зависимости от результата сравнения, поиск продолжается в одном из дочерних узлов (левом или правом).
- Если текущий узел ближе к искомой точке, чем уже найденные соседи, он добавляется в список лучших соседей.
Обновление списка лучших соседей:
- Если количество найденных соседей меньше заданного максимума, или если текущий узел ближе, чем самый дальний из уже найденных, он добавляется в список.
- Если список заполнен, удаляется самый дальний сосед, чтобы освободить место для нового.
Проверка других поддеревьев:
- После проверки одного из дочерних узлов, если расстояние до текущего узла позволяет, происходит проверка другого дочернего узла. Это необходимо для того, чтобы убедиться, что не пропущены более близкие соседи.

Выводы

В этом уроке мы познакомились с KD-деревьями, которые помогают организовать хранение пространственных данных. KD-деревья — это основная альтернатива методам машинного обучения при решении кластеризационных задач.

Поиск ближайших соседей — это одна из популярных задач, стоящих перед программистами. Результаты ее решения нужны в медицине, геологии, картографии и прочих прикладных областях, связанных с кластеризацией пространственных объектов.

Каталог

Полный список доступных курсов по разным направлениям

Навигация по темеТеория

Завершено

0 / 8