Алгоритмы на деревьях
Теория: B-деревья
Ранее в курсе мы уже познакомились со сбалансированными деревьями поиска — это АВЛ-деревья или красно-черные деревья.
Они способны организовать эффективный поиск элементов за время logN. Но чтобы совершить этот поиск, потребуется выполнить logN операций. Со временем число данных, которые нужно хранить в дереве, будет расти. Дерево потребуется сохранять на более дешевых хранилищах данных вроде жестких дисков, а не хранить в оперативной памяти.
Это ведет к тому, что для поиска элемента в дереве нам придется logN раз обратиться к жесткому диску. При больших N это число операций остается существенным. Операции над жестким диском гораздо медленнее, чем над оперативной памятью. Значит, оборудование будет быстро изнашиваться, а само приложение будет работать медленнее.
Ученым предстояло решить, как организовать эффективный поиск в древовидных структурах, которые должны храниться в постоянной памяти. Чтобы решить эту задачу, они придумали новый вид деревьев — сильноветвящиеся B-деревья и их производные: B+ деревья, B*-деревья, 2-3 деревья.
В этом уроке мы детально познакомимся с видами сильноветвящихся деревьев и особенностями реализации операций поиска, вставки и удаления узлов.
Устройство B-деревьев
Рассмотрим дерево, которое состоит из миллиона элементов. Если хранить данные в сбалансированном бинарном дереве поиска, то поиск элемента займет двадцать операций:
log2(1000000) = 19,932
Если разбить дерево на страницы, в каждой из которых будет по семь узлов дерева, поиск поддерева с нужным элементом будет выполнен за семь обращений к диску:
log(7+1) 1000000 = 6,644
Рассмотрим пример такого разбиения:
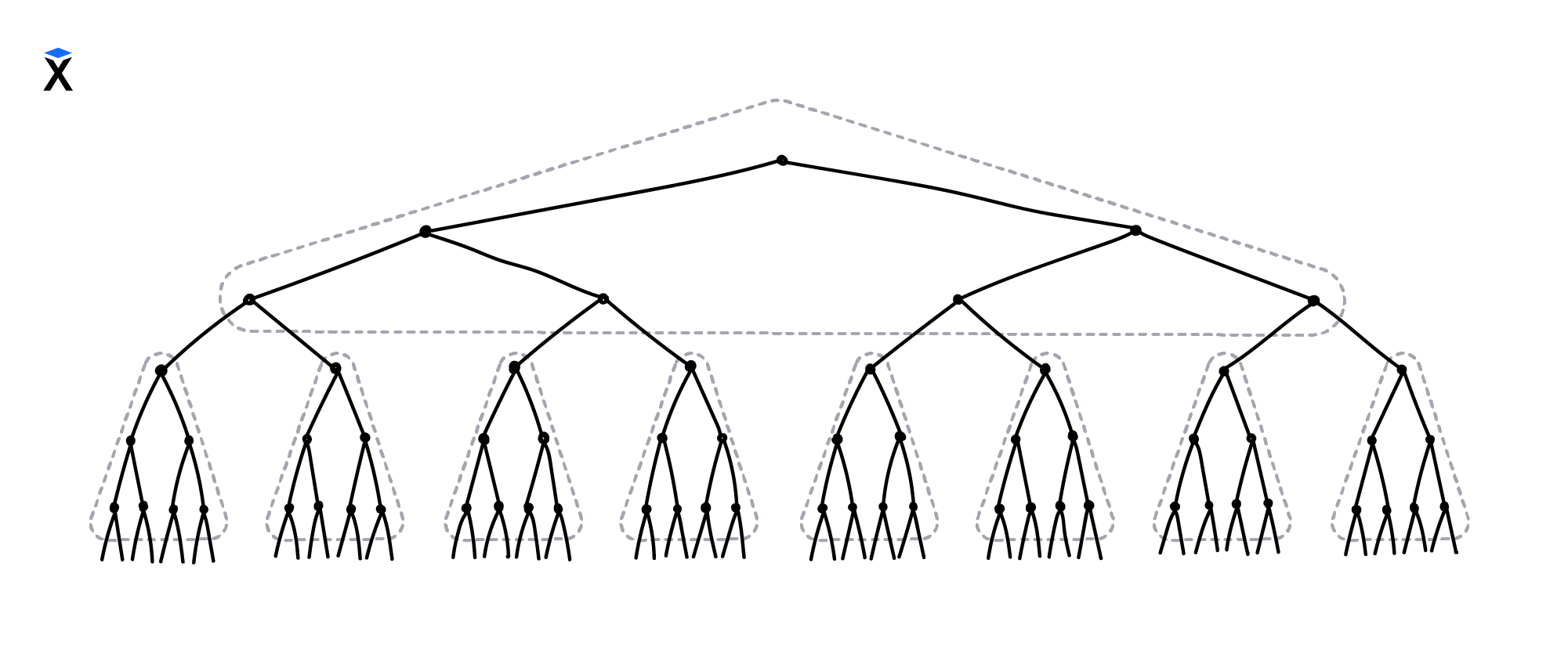
Такая группировка узлов на страницах превращает бинарное дерево в октарное — с восемью дочерними узлами. Число дочерних узлов у страницы может и дальше увеличиваться, например, до 128 элементов. Это приведет к тому, что поиск элемента будет выполнен всего за три обращения к диску:
log128(1000000) = 2,847
Таким образом, нам достаточно выбрать оптимальный размер страницы, который удовлетворяет нашим ограничениям по оперативной памяти. Также мы можем хранить в оперативной памяти ссылку на корневой элемент дерева, а сам вид дерева можно привести к виду на рисунке:
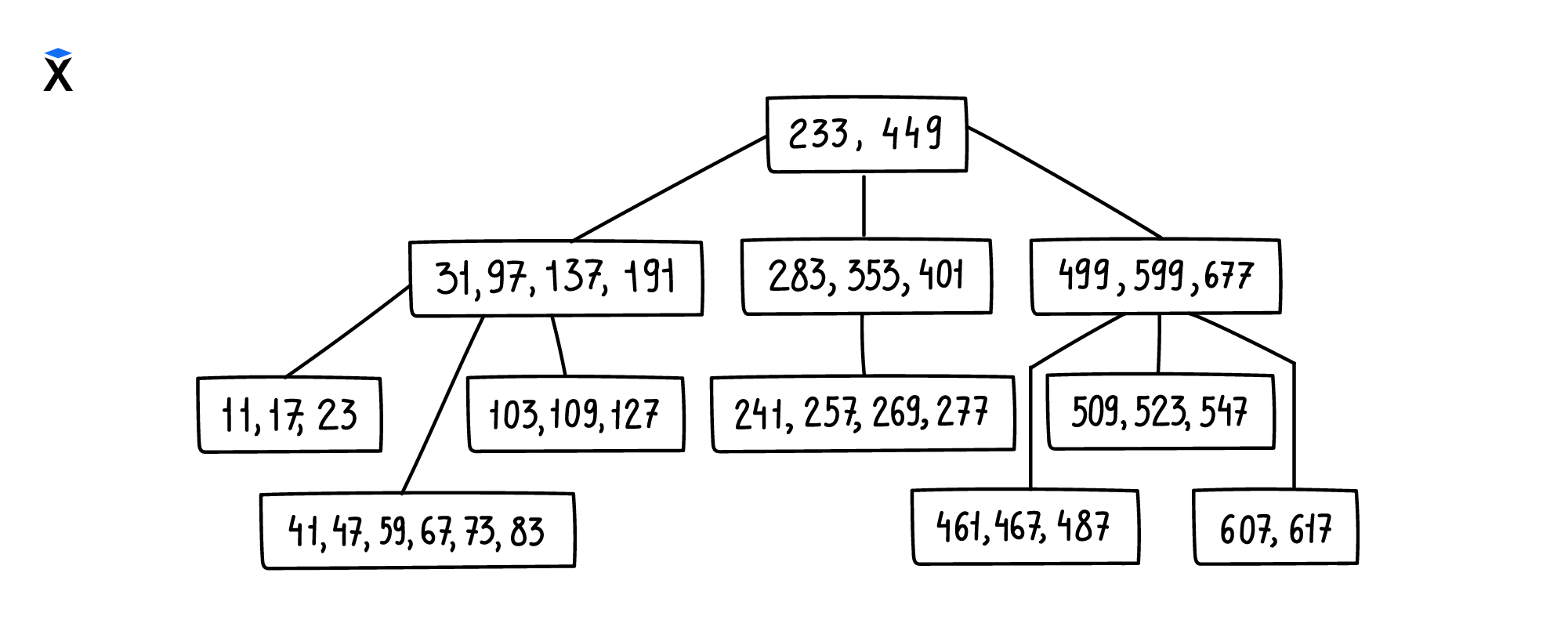
В этом случае в узлах располагается несколько ключей в порядке возрастания слева направо. Дочерние узлы содержат ключи, которые находятся в промежутке между значениями родительского узла.
Помимо особенности расположения ключей стоит отметить, что B-дерево со степенью m обладает следующими свойствами:
- Глубина всех листьев одинакова
- Каждый узел имеет не более
mпотомков - Каждый узел кроме корневого и листовых имеют не менее
m/2потомков - Если высота дерева больше единицы, то у корневого узла не менее двух дочерних узлов
- Нелистовой узел с
kпотомками имеетk-1ключей
Представим узел B-дерева в виде кода на JavaScript:
Над B-деревьями выполняются все классические операции:
- Поиск узла
- Добавление узла
- Удаление узла
Однако сложная организация ветвления узлов вносит свои реализации. Далее рассмотрим эти операции подробнее.
Операции над B-деревьями
Поиск узлов в случае работы с B-деревом отличается от аналогичной операции над бинарным деревом только порядком действий во время проверки ключей узла. Он будет выглядеть следующим образом:
В этом примере можно заметить пересечение с логикой поиска в бинарном дереве поиска. Если искомое значение меньше текущего значения узла, мы переходим по левой от него ветке. Если больше всех ключей узла — переходим на правое поддерево.
Вставка новых элементов в B-дерево разрешается только в листовые узлы. Это приводит к необходимости следить за заполненностью узлов. Если при вставке превысилась максимальная степень узла, то узел нужно разделять на части.
Чтобы разделить узел, создается два новых листовых узла, которые содержат половину значений из существующего узла, и переносится среднее значение в родительский узел.
Если заполнен и корневой узел, то мы разбиваем его на два новых: выбираем среднее значение, создаем для него новый узел, который станет новым корнем всего дерева:
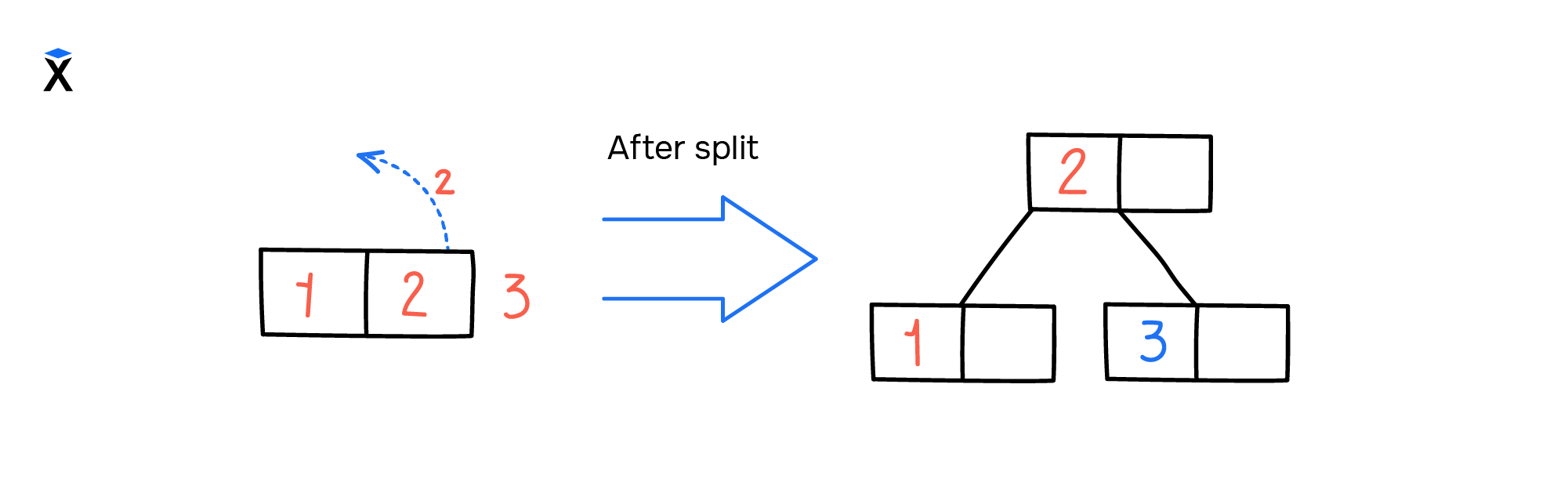
В данном примере мы вставляем ключ 3 в дерево с одним заполненным корневым узлом. Вставка ключа приводит к переполнению корневого узла. Чтобы решить эту ситуацию, мы разбиваем корневой узел на две части, создаем новый узел со средним значением и делаем его корнем всего дерева.
Аналогично изменение структуры узлов может возникнуть, когда узел удаляется. Если в соседних узлах слишком мало ключей — занятость узлов падает ниже значения m/2 — и эти узлы находятся на одном родственном уровне, то такие узлы необходимо слить. Данная ситуация называется антипереполнением.
Существует два способа объединения узлов:
- Если у двух смежных узлов общий предок, и их содержимые помещаются в один узел, их следует объединить
- Если содержимое смежных узлов не помещается в одном узле, то ключи перераспределяются между ними, чтобы восстановить баланс
Операции слияния и расщепления достаточно дорогостоящие. Чтобы оптимизировать данный процесс, были придуманы специальные подвиды B-деревьев.
Производные виды деревьев
К производным видам B-деревьев чаще всего относят следующие три вида:
- B⁺-деревья
- B*-деревья
- 2-3-деревья
B⁺-деревья
В B⁺-деревьях данные ключей хранятся только в листовых узлах, а в промежуточных хранятся копии значений ключей. Это помогает эффективно организовывать поиск в блочных средах хранения. Например, в файловых системах, где B⁺-деревья применяют, чтобы хранить каталоги.
Также реляционные системы управления базами данных, такие как DB2, Informix, Microsoft SQL Server, Oracle, поддерживают этот тип деревьев, чтобы организовывать табличные индексы.
B*-деревья
B*-дерево ориентировано на более плотное хранение ключей во внутренних узлах. Этот вариант гарантирует, что некорневые узлы заполнены как минимум на две трети от m вместо половины от m.
B*-деревья используются для того, чтобы вызывать дорогостоящую операцию разделения как можно реже. Чтобы достичь этого, вместо немедленного разделения узла при его заполнении, его ключи «переливаются» в соседний узел. Если же и соседний узел заполнен, то ключи приблизительно поровну разделяются на три новых узла.
2-3-деревья
2-3 деревья — частный случай B⁺-деревьев с сокращенным количеством элементов на страницах. Каждый узел 2-3-дерева, кроме листовых, может содержать только один ключ и два потомка, либо два ключа и три потомка.
Выводы
Способ хранения деревьев может оказывать существенное влияние на организацию структуры узлов и входящих в них ключей. Например, хранение классических бинарных деревьев поиска на жестком диске может привести к многократному росту числа операций над диском.
Для оптимизации хранения и поиска данных в таких условиях были предложены B-деревья. Они помогают сократить нагрузку на диск. Это возможно, если увеличить количество веток в узлах и хранить несколько ключей полезной нагрузки.
