Интереснее всего изучать алгоритмы не сами по себе, а вместе с Разрабатывая игру, мы изучаем эффективные алгоритмы и интересные структуры данных.Представим, что мы разрабатываем игру. Мы хотим написать алгоритм, который приведет персонажа (в синем кружке) к важному ресурсу (в красном кружке):
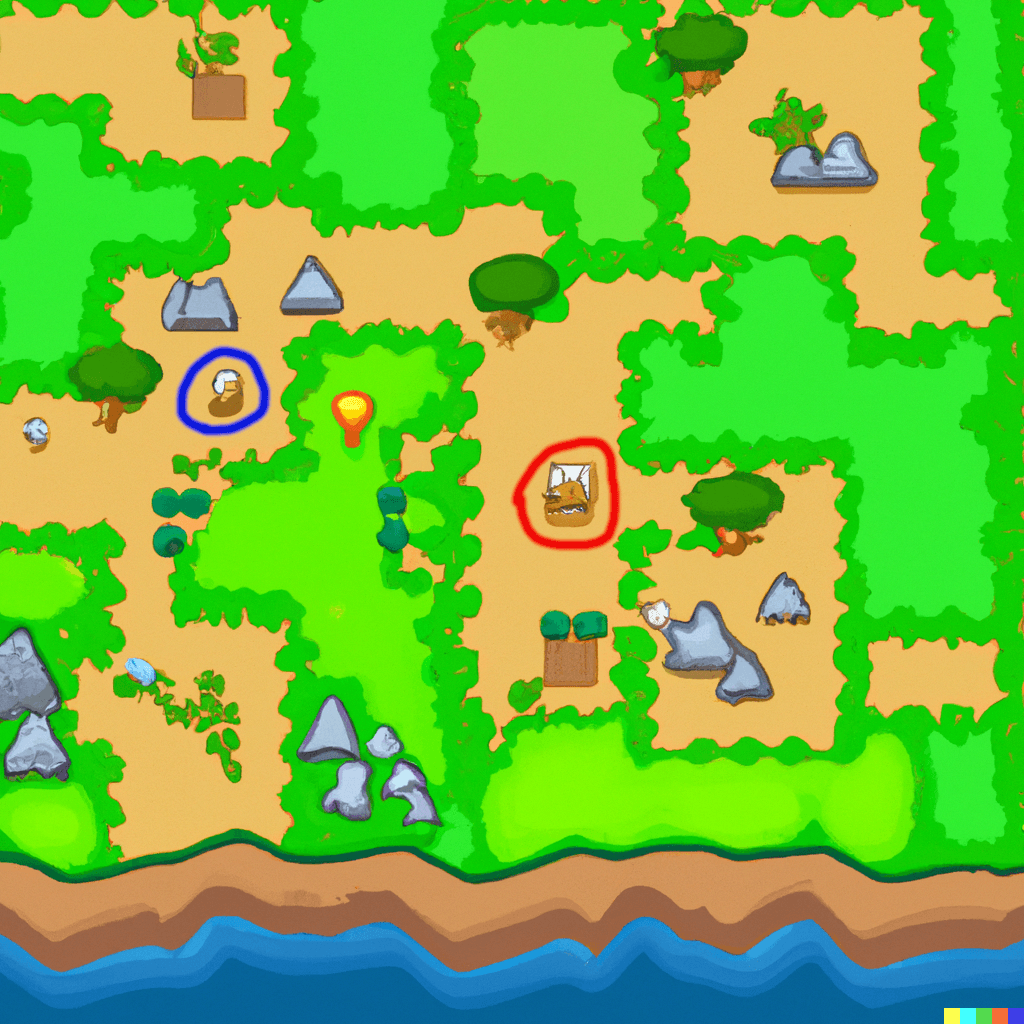
Компьютер должен проложить кратчайший маршрут с учетом всех препятствий. Здесь поможет обход графа в ширину, с которым мы познакомимся в этом уроке. Также этот алгоритм называют «алгоритмом поиска в ширину» или BFS (breadth first search).
Карты в играх похожи на шахматную доску — они состоят из отдельных клеток. Клетки могут быть:
-
Проходимыми — дорога, чистое поле, тропинка
-
Непроходимыми — река, лес, гора
Обычно юниты могут ходить влево, вправо, вверх и вниз, но иногда в играх разрешают движение по диагонали. Задачу усложняют препятствия, которые превращают карту в подобие лабиринта. Поэтому нам нужно, чтобы алгоритм построил маршрут в виде цепочки клеток. В нашем случае она выглядит так:
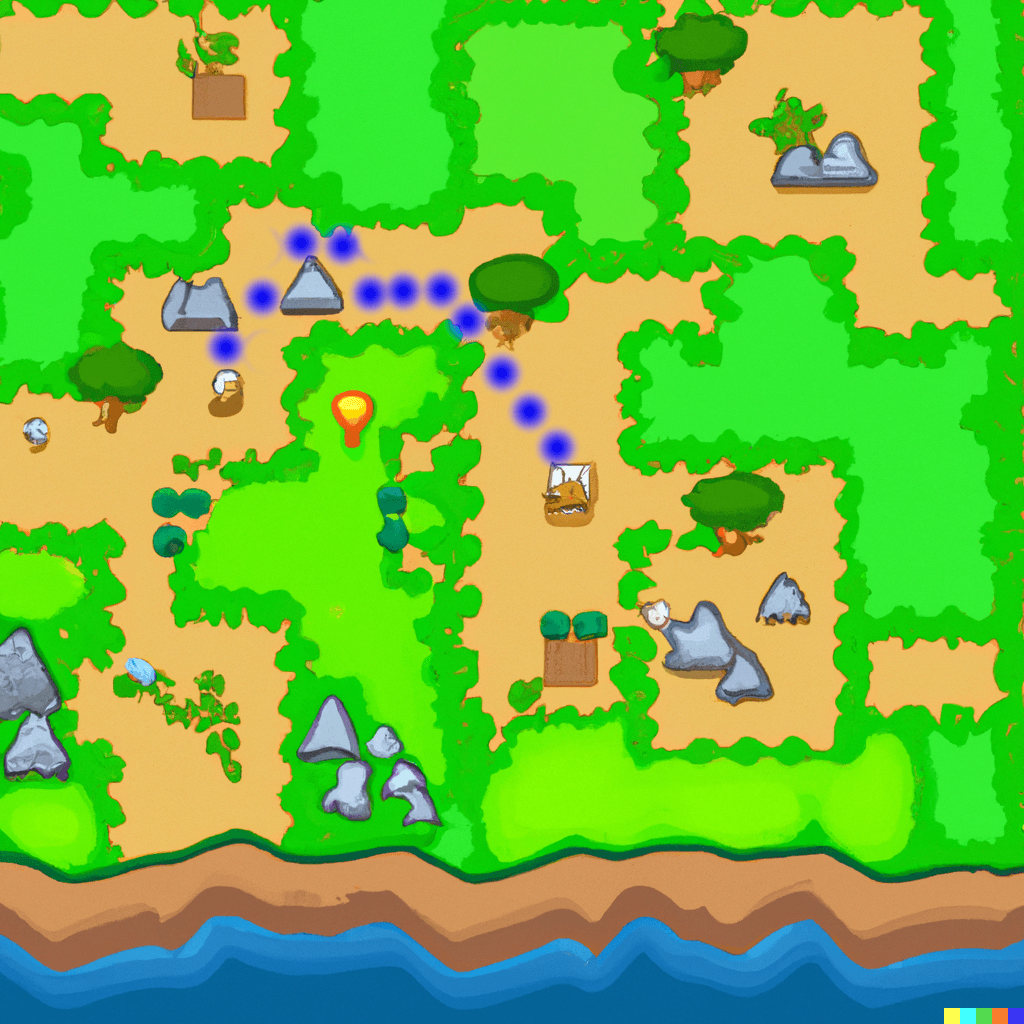
Обход в ширину
При поиске в глубину мы проверяем соседнюю вершину, далее — ее соседнюю вершину, и таким образом продвигаемся от исходной точки. А при поиске в ширину мы двигаемся по-другому: равномерно во все стороны, проверяя сначала ближайшие вершины, затем — следующие за ними и так далее.
Возьмем карту с персонажем, которого нужно провести к ресурсу. Перенесем ее на схему и продумаем алгоритм:
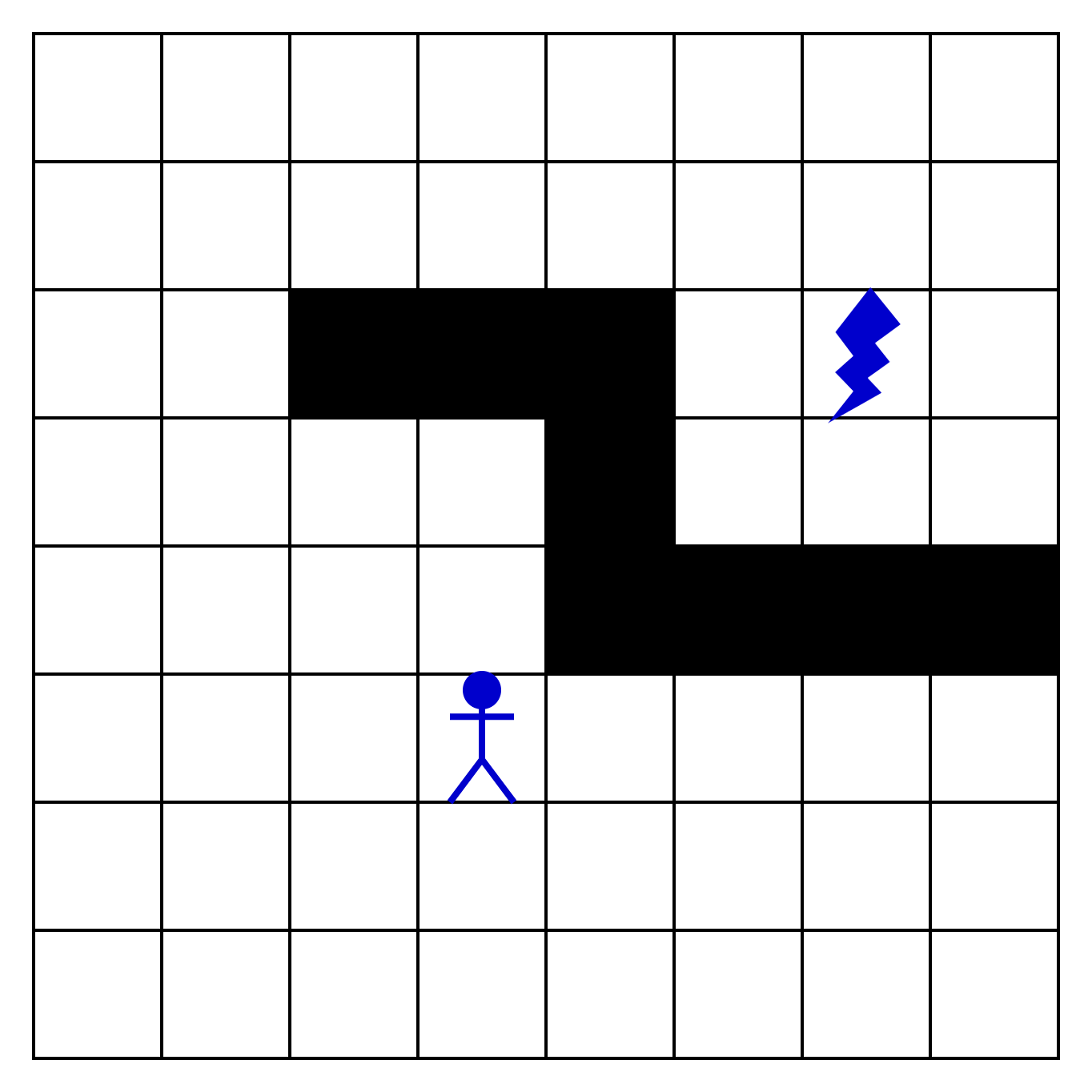
На первом шаге мы осматриваем соседние клетки. В нашей игре юнит может двигаться только вверх, вниз, вправо и влево. Если в соседних клетках нет ресурса, то двигаемся дальше и осматриваем соседей:
На серии рисунков показано, какие вершины оказываются в области видимости алгоритма. Чтобы не загромождать урок похожими рисунками, мы оставили только каждый второй шаг:
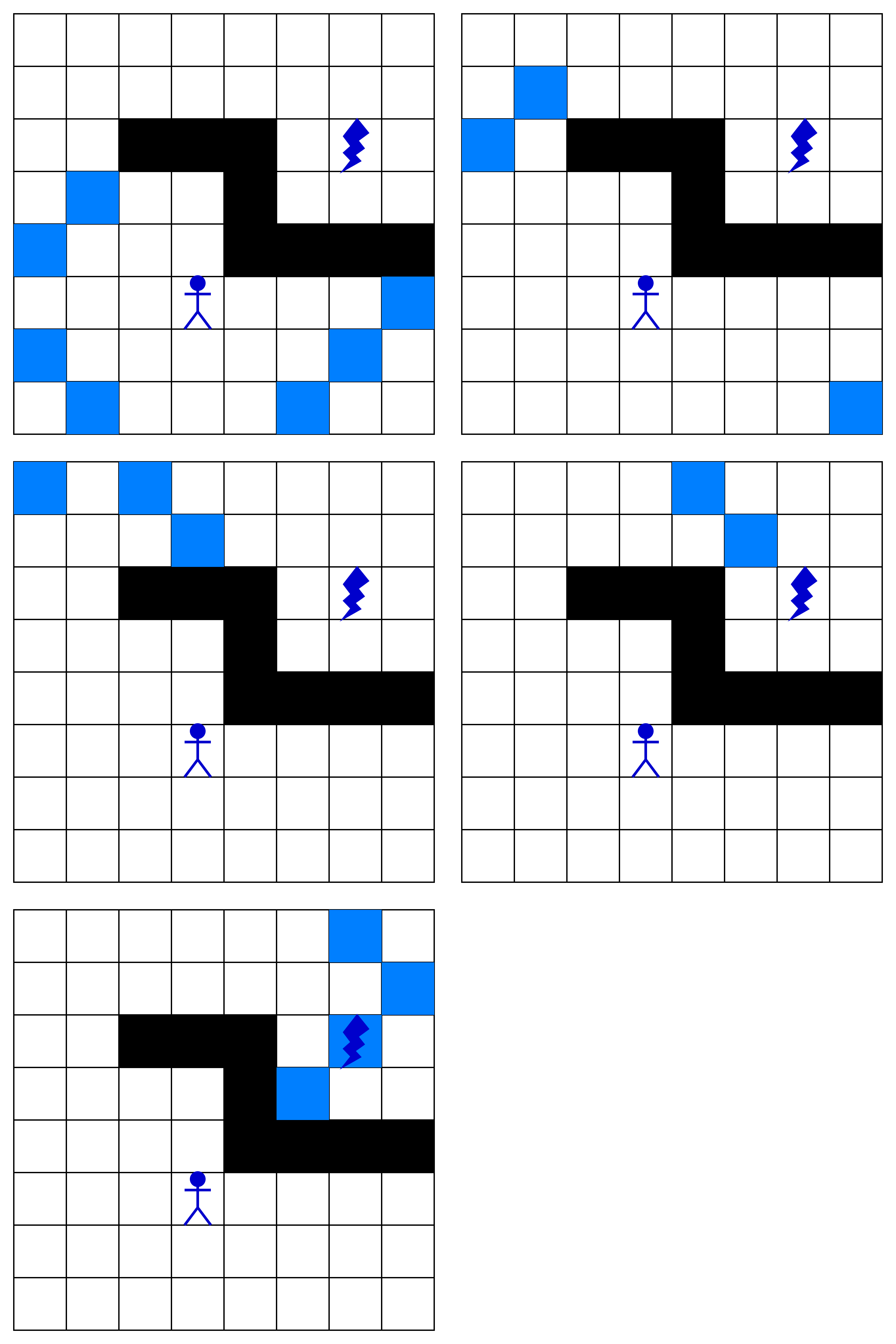
На очередном шаге мы добираемся до нашего ресурса — поиск закончен. Двигаясь назад по клеткам, мы можем восстановить путь:
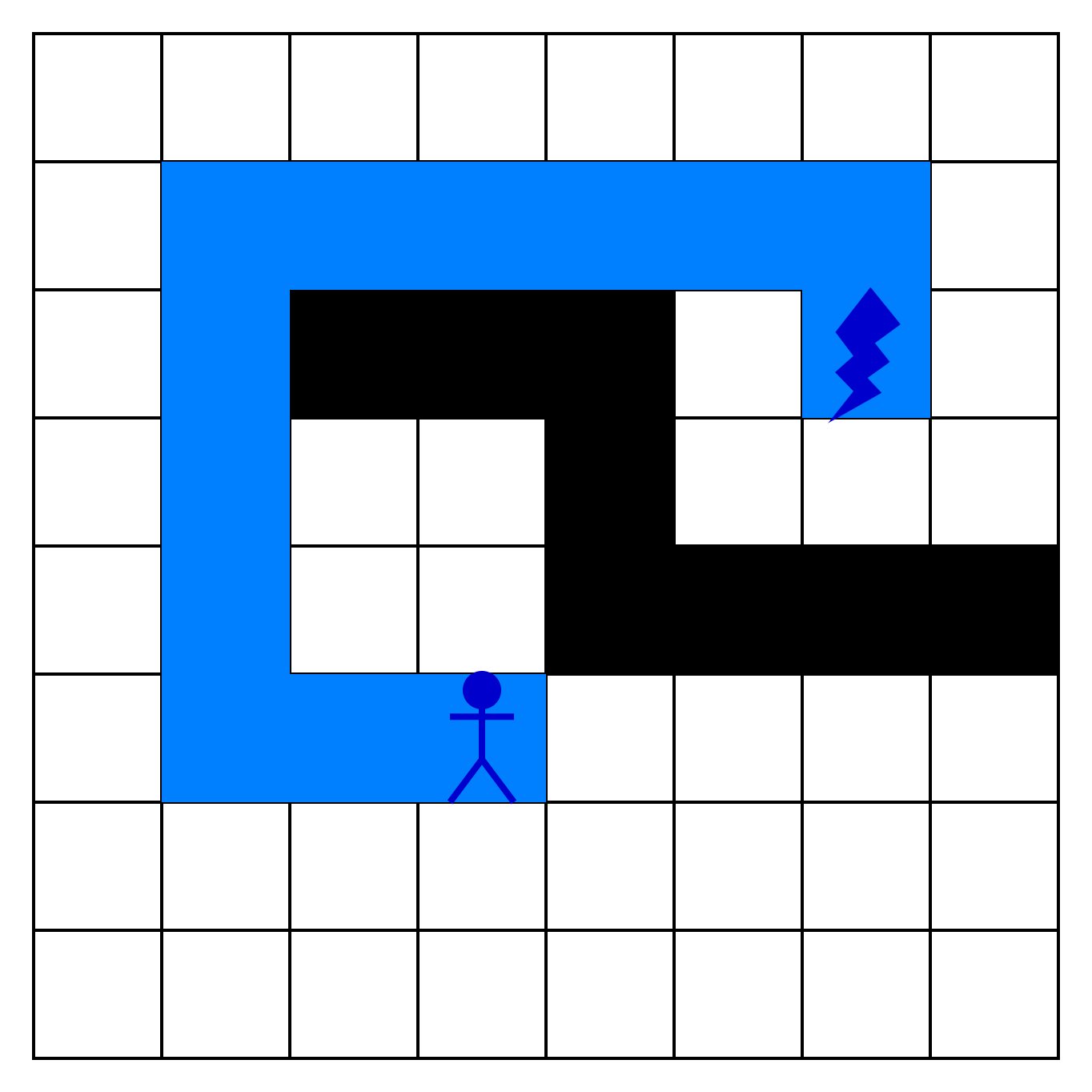
В целом, идея алгоритма кажется ясной, но как именно искать соседей на каждом шаге? Разберемся в деталях:
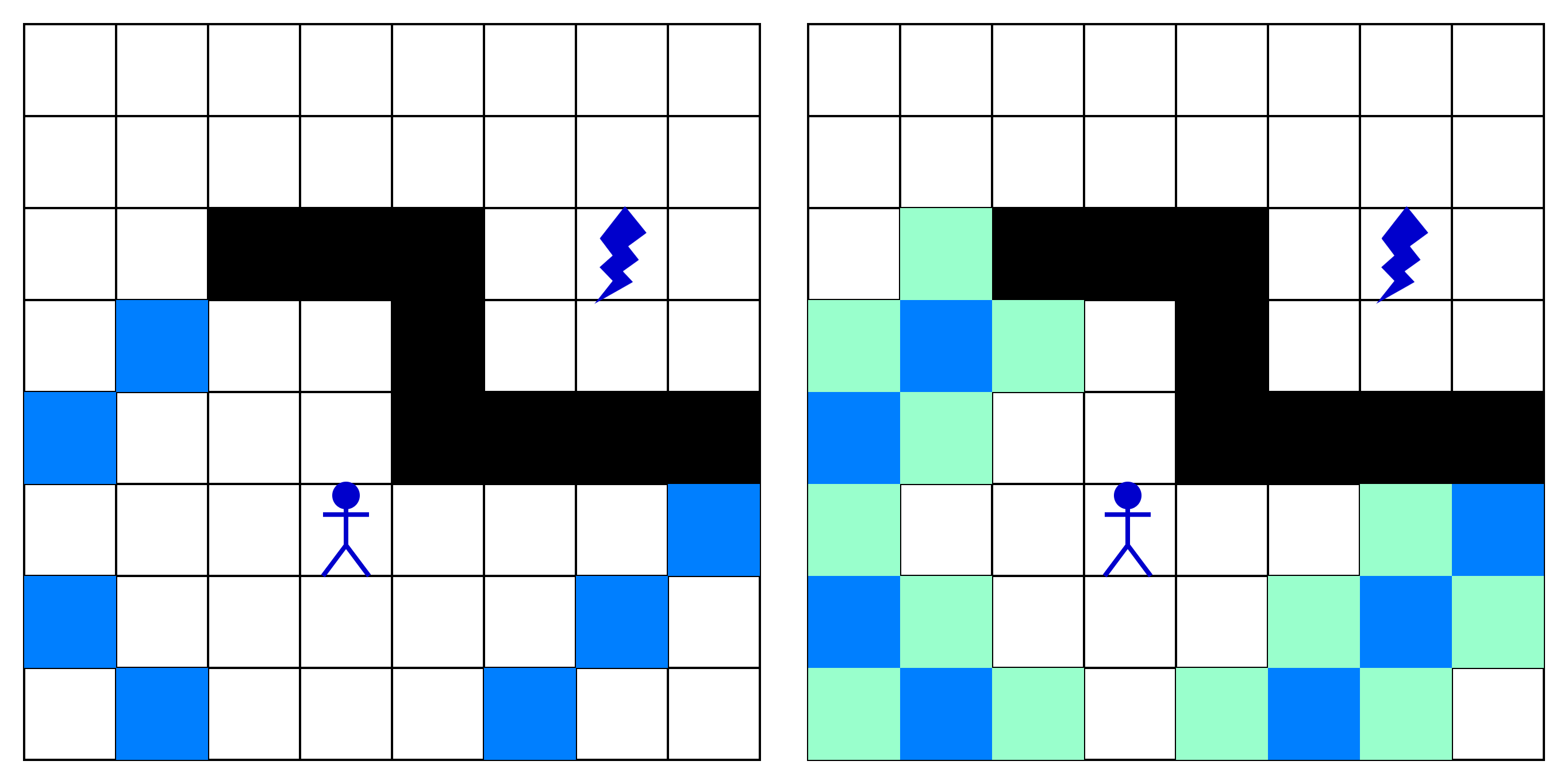
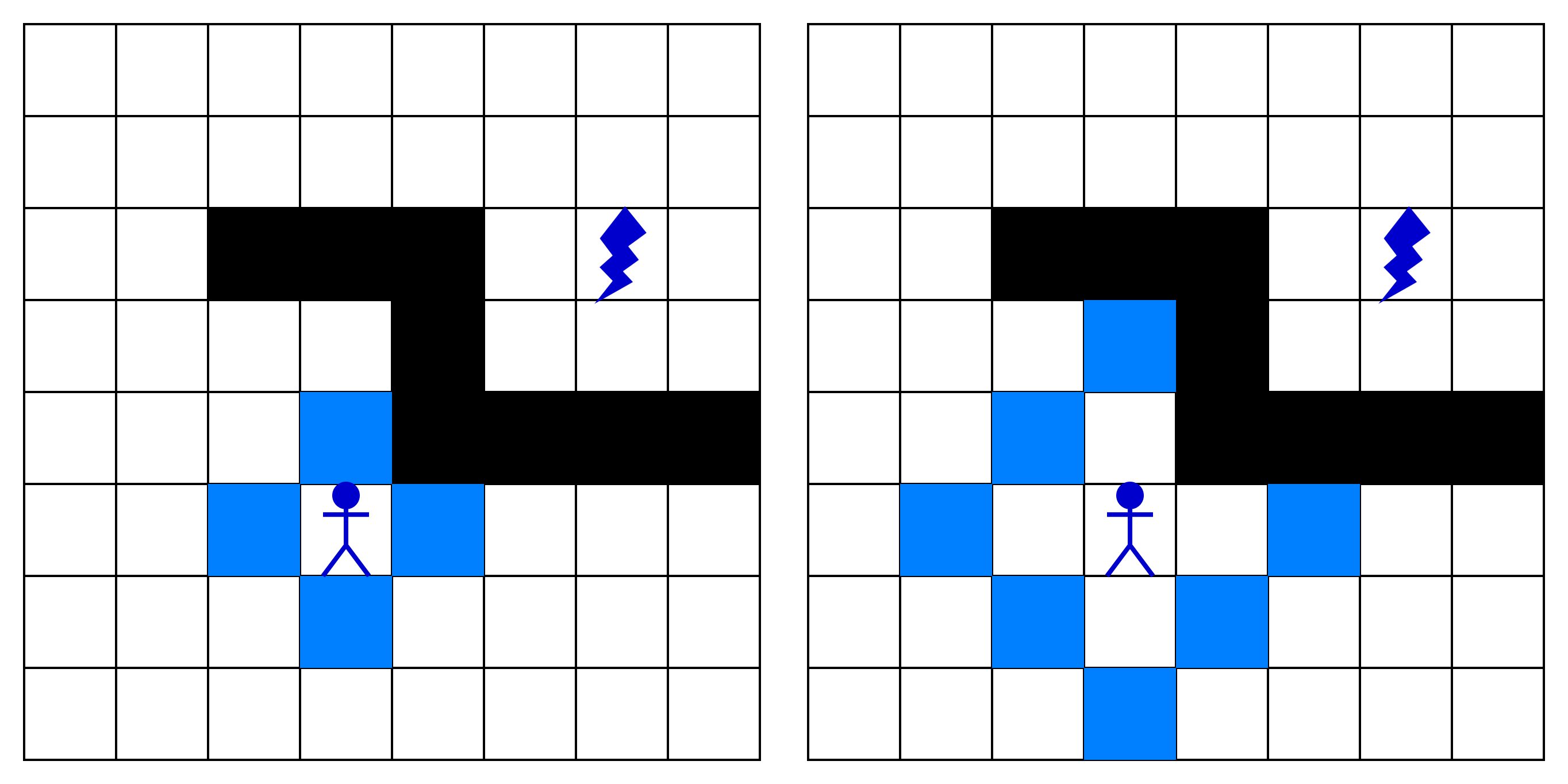
В качестве примера возьмем один из шагов алгоритма, показанный на рисунке слева. На нем мы видим:
-
Синие клетки — те, которые мы проверяем на текущем шаге
-
Светло-зеленые клетки — клетки, которые находятся по соседству от синих (сверху, снизу, справа и слева от них)
Некоторые из них проверять не нужно, потому что мы проверяли их на предыдущем шаге. Другие клетки могут встречаться в списке более двух раз, потому что они находятся, например, слева от одной клетки и сверху от другой:
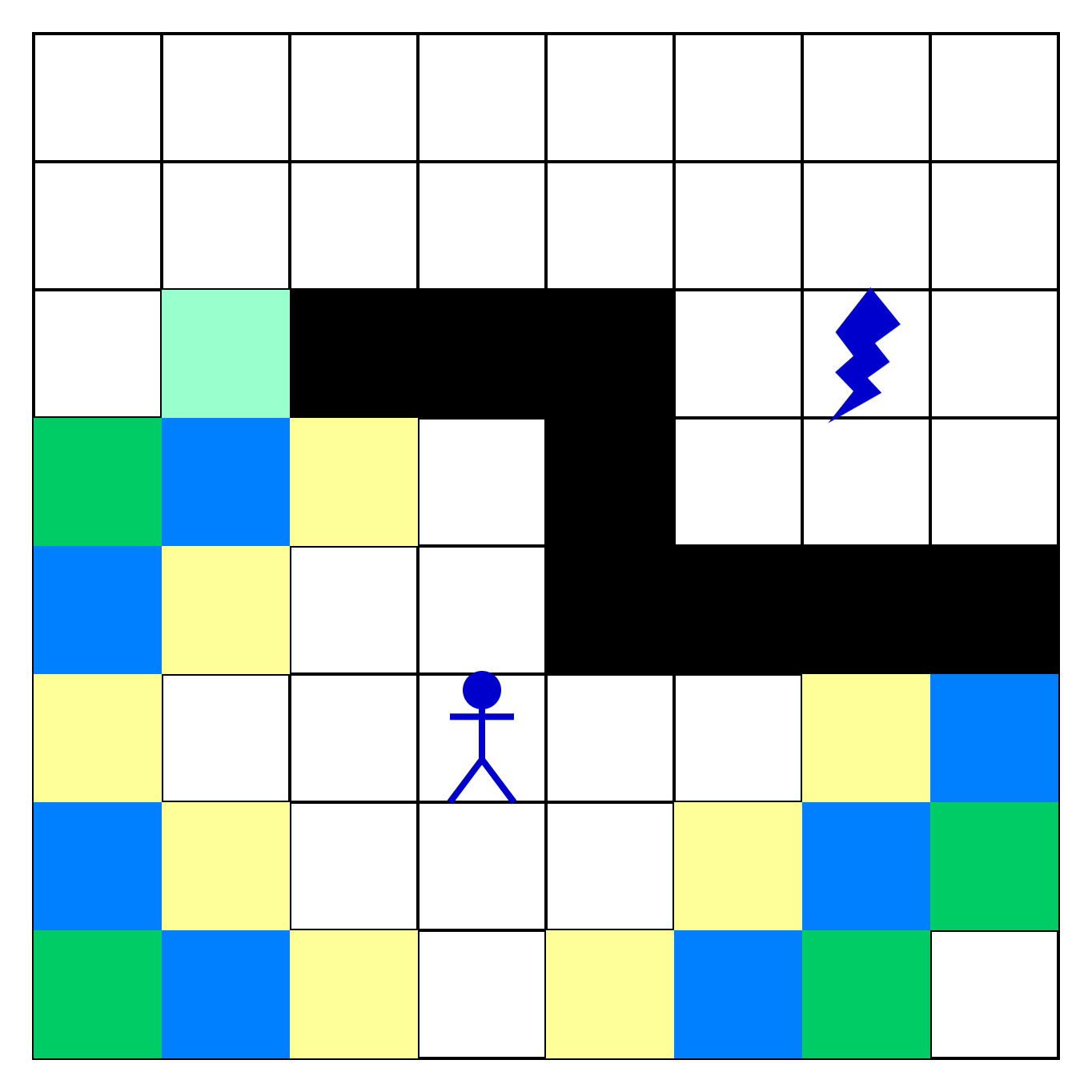
Для наглядности закрасим:
-
Желтым цветом — уже проверенные клетки
-
Темно-зеленым — клетки, которые одновременно являются соседями двух и более клеток
В программе нам потребуется два множества. В первое мы будем добавлять уже просмотренные желтые клетки.
Если новая соседняя клетка обнаружится в этом множестве, значит, мы ее уже проверяли. Таких соседей мы будем пропускать.
Оставшиеся клетки будем добавлять во второе множество. Элементы в множестве встречаются не больше одного раза, поэтому одну и ту же клетку можно добавлять много раз — она останется в единственном экземпляре. Опираясь на цвета клеток, можем сказать, что во второе множество попадают все зеленые клетки: и светлые, и темные.
Неявные графы
Нам осталось разобраться, как получить граф из карты. Карта — это двумерный массив клеток. В каждом элементе хранится код, который определяет, что находится в клетке. Например, 0 может означать дорогу, 1 — гору, 2 — лес, и так далее.
Кажется, что для поиска в ширину нужно что-то вроде списка смежности из предыдущего урока. Но на карте соседей клетки можно определить, зная только ее координаты:
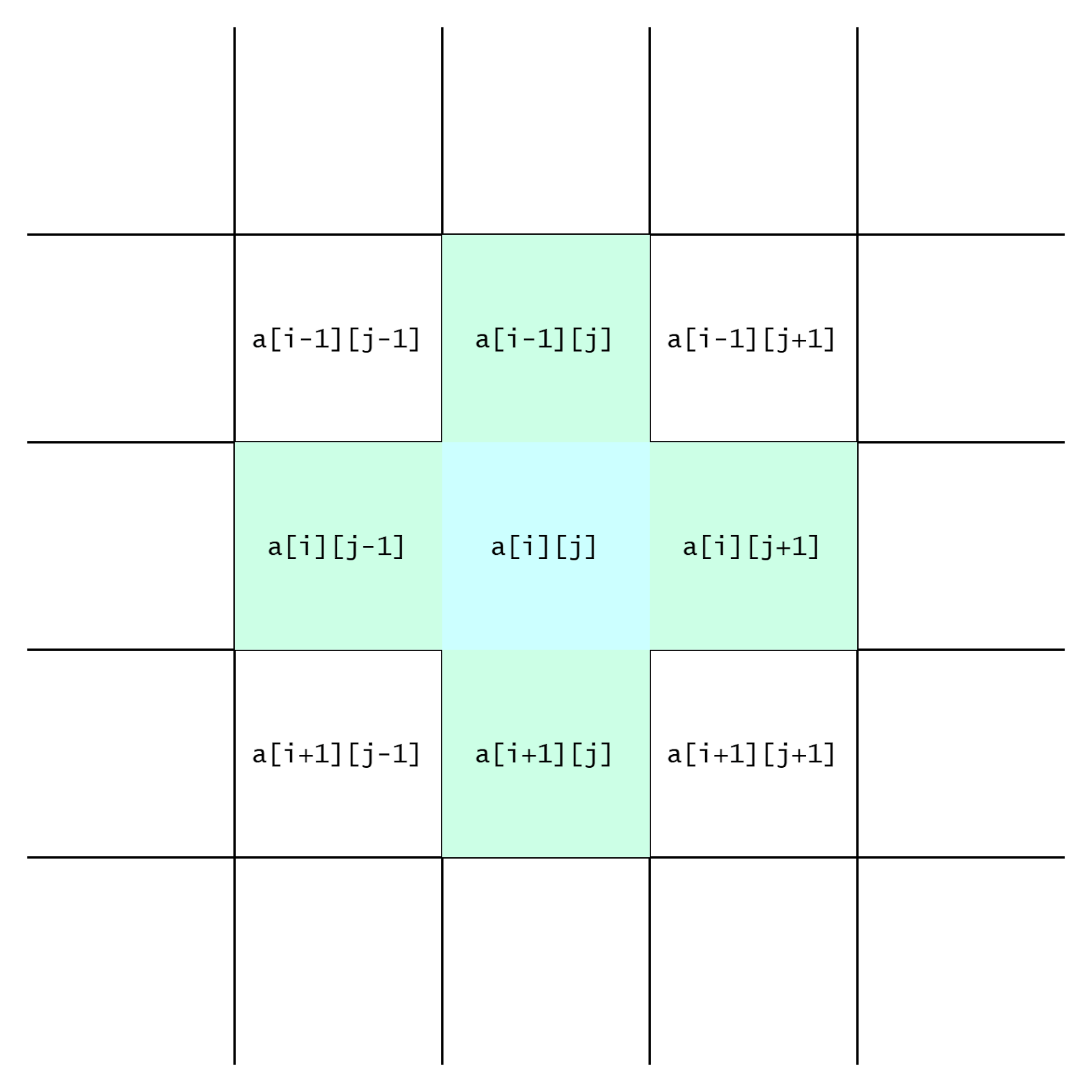
Из рисунка видно, что по соседству с голубой клеткой a[i][j] находятся четыре зеленые клетки с такими координатами:
-
a[i - 1][j] -
a[i][j - 1] -
a[i][j + 1] -
a[i + 1][j]
Эти координаты можно вычислить, но при этом нужно учитывать два обстоятельства.
Во-первых, не у каждой клетки есть соседи: например, у клеток в верхней строке нет соседей сверху, а у клеток в левом столбце — соседей слева. Во-вторых, мы должны рассматривать только проходимые клетки — с кодами, соответствующими дороге, тропинке или чистому полю.
Чтобы идентифицировать вершину, нам достаточно пары чисел, а именно строки и столбца клетки. При этом нам не надо в явном виде хранить вершины или ребра графа.
Если соседние вершины можно вычислить на основании дополнительной информации, то мы говорим, что граф представлен в неявном виде — речь идет о неявном графе.
Реализация
Для поиска в ширину мы реализовали функцию bfs(), что означает breadth first search:
const bfs = (map, fromRow, fromColumn, toRow, toColumn) => {
const pack = (row, column) => `${row}:${column}`;
const unpack = (cell) => cell.split(':').map((x) => parseInt(x, 10));
const visited = new Set();
const isValidNeighbour = (row, column) => {
if (row < 0 || row >= map.length) {
return false;
}
if (column < 0 || column >= map[row].length) {
return false;
}
const cell = pack(row, column);
if (visited.has(cell)) {
return false;
}
return map[row][column] === 0;
};
let step = new Map();
const initialCell = pack(fromRow, fromColumn);
step.set(initialCell, [initialCell]);
while (step.size > 0) {
const nextStep = new Map();
const tryAddCell = (row, column, path) => {
if (isValidNeighbour(row, column)) {
const cell = pack(row, column);
const newPath = [...path];
newPath.push(cell);
nextStep.set(cell, newPath);
visited.add(cell);
}
};
for (const [cell, path] of step) {
const [row, column] = unpack(cell);
if (row === toRow && column === toColumn) {
return path;
}
tryAddCell(row - 1, column, path);
tryAddCell(row + 1, column, path);
tryAddCell(row, column - 1, path);
tryAddCell(row, column + 1, path);
}
step = nextStep;
}
return null;
};На вход функция получает пять параметров:
-
Карту (
map) -
Исходные координаты (
fromRow,fromColumn) -
Координаты цели (
toRow,toColumn)
Карта — это двумерный прямоугольный массив с числами. Функция предполагает, что 0 означает проходимую клетку (дорогу), а все остальные числа означают непроходимые клетки (гору, лес, озеро).
Сложность в том, что координаты — это пара чисел строка и столбец. Мы не можем использовать их, как ключ множества или словаря, потому что ключ — это одно значение. Мы могли бы сложить их в такой объект { row: 5, column: 3 }. Но, к сожалению, это простое решение в JavaScript работает неправильно.
В JavaScript два разных объекта считаются разными, даже если их поля и значения полей совпадают:
const a = { row: 5, column: 3 };
const b = { row: 5, column: 3 };
console.log(a === b); // => falseЧтобы обойти это ограничение, мы будем упаковывать координаты в строку — это поможет нам проверять уникальность координат. Перед использованием мы будем распаковывать координаты из строки:
const pack = (row, column) => `${row}:${column}`;
const unpack = (cell) => cell.split(':').map((x) => parseInt(x, 10));Упаковка сводится к тому, что мы соединяем два числа в строку, связав их двоеточием. Координаты 5 и 3 превращаются в строку 5:3.
Распаковка выполняет обратное преобразование — извлекает части строки, разделенные двоеточием и превращает в числа.
Весь алгоритм поиска представляет собой один большой цикл. Перед циклом мы создаем пустое множество visited, куда будем помещать клетки, которые мы уже посетили. Функция isValidNeighbour проверяет, является ли клетка с указанными координатами нормальным соседом:
const isValidNeighbour = (row, column) => {
if (row < 0 || row >= map.length) {
return false;
}
if (column < 0 || column >= map[row].length) {
return false;
}
const cell = pack(row, column);
if (visited.has(cell)) {
return false;
}
return map[row][column] === 0;
};Клетка считается доступной для посещения, если она не выходит за границы карты, если мы ни разу ее не посещали и если в ней хранится код 0, который соответствует непроходимому участку карты.
Клетки, которые мы рассматриваем на каждом шаге алгоритмы, хранятся в словаре step. В самом начале мы помещаем туда единственную клетку — ту, с которой начинаем поиск. В качестве значения помещаем массив, в котором хранится путь. В начале путь — это наша единственная клетка:
let step = new Map();
const initialCell = pack(fromRow, fromColumn);
step.set(initialCell, [initialCell]);На каждом шаге алгоритма мы убеждаемся, что в словаре step есть клетки. Если словарь пуст, значит, мы осмотрели все клетки, до которых могли добраться и не нашли пути. В этом случае возвращаем null.
Если клетки в словаре есть, готовим следующий шаг. Для этого используем вспомогательную функцию tryAddCell:
const nextStep = new Map();
const tryAddCell = (row, column, path) => {
if (isValidNeighbour(row, column)) {
const cell = pack(row, column);
const newPath = [...path];
newPath.push(cell);
nextStep.set(cell, newPath);
visited.add(cell);
}
};Мы создаем новый словарь, куда будем заносить клетки на следующем шаге. Функция tryAddCell проверяет, что клетка с переданными ей координатами — нормальный сосед. Если это так, добавляет ее к уже построенному пути и к множеству посещенных клеток:
for (const [cell, path] of step) {
const [row, column] = unpack(cell);
if (row === toRow && column === toColumn) {
return path;
}
tryAddCell(row - 1, column, path);
tryAddCell(row + 1, column, path);
tryAddCell(row, column - 1, path);
tryAddCell(row, column + 1, path);
}
step = nextStep;Наконец, основной цикл. Мы извлекаем все клетки и соответствующие им пути с текущего шага и проверяем, не добрались ли мы до конца. Если добрались, сразу возвращаем путь.
В противном случае пытаемся добавить в словарь для следующего шага клетку сверху, снизу, слева и справа от текущей.
В конце концов подменяем старый словарь step новым словарем nextStep. Посмотрим, как работает алгоритм:
const map = [
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 1, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 1, 1, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0]
];
console.log(bfs(map, 5, 3, 2, 6)); // =>
[
// '5:3', '4:3', '3:3',
// '3:2', '3:1', '2:1',
// '1:1', '1:2', '1:3',
// '1:4', '1:5', '2:5',
// '2:6'
// ]https://replit.com/@hexlet/algorithms-graphs-bfs
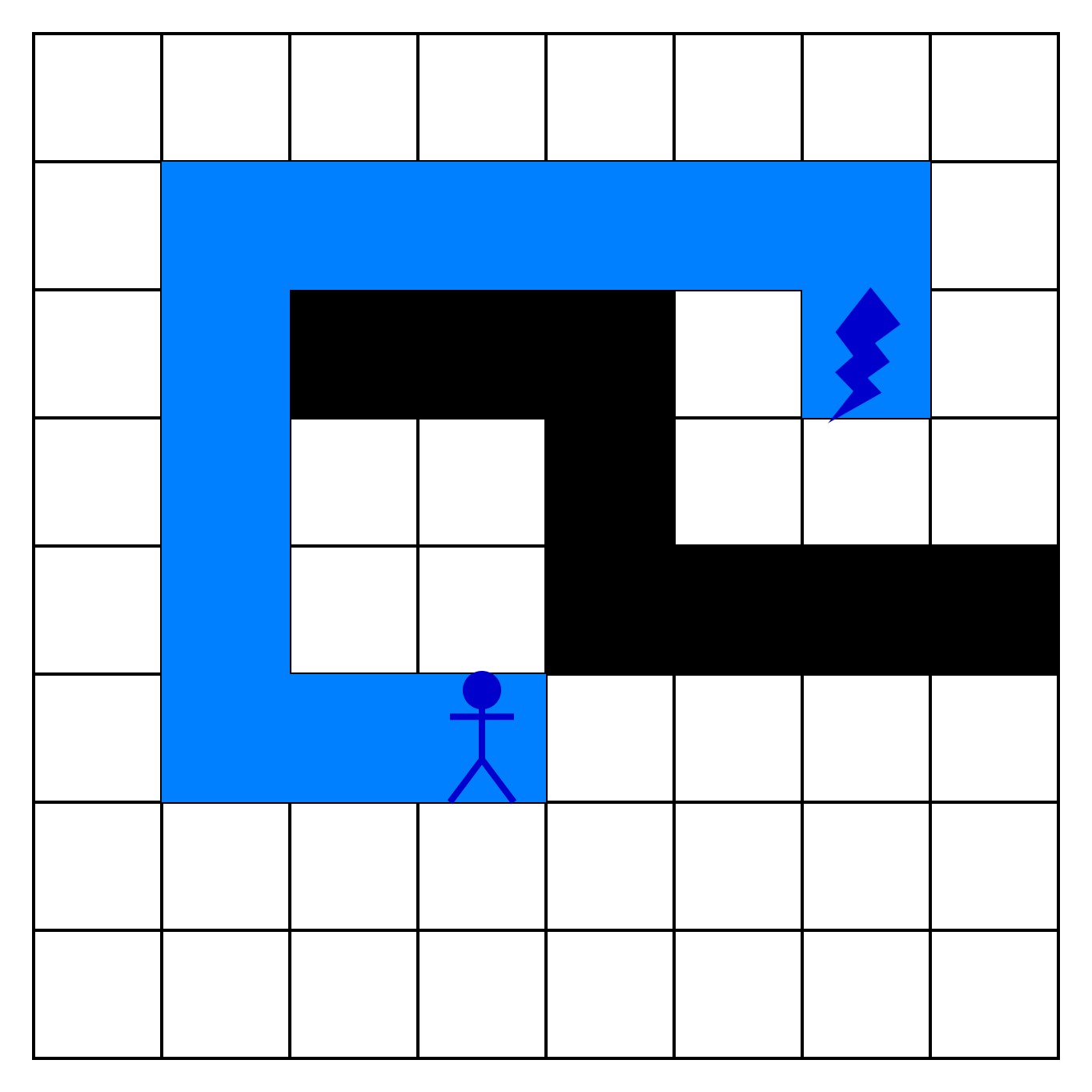
Как видим, алгоритм поиска в ширину нашел короткий путь.
Выводы
Повторим ключевые выводы этого урока:
-
Алгоритм поиска в ширину используется в компьютерных играх, чтобы прокладывать кратчайший маршрут на двумерной карте. По-английски алгоритм называется BFS, что означает breadth first search (поиск сначала вширь)
-
В отличие от поиска в глубину, поиск в ширину сначала перебирает ближайшие вершины, затем ближайшие к ближайшим, и так далее
-
Если, благодаря знаниям о задаче, мы можем определять соседние вершины, то можно не хранить граф в явном виде (например, в виде списков смежности)
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
