В прошлом уроке мы познакомились с классами сложности задач и выяснили, что строгие алгоритмы практически неприменимы для задач класса NP.
Однако эти задачи все равно приходится решать: составлять расписания, распределять грузы и строить маршруты. Как именно программисты справляются со сложными задачами? Они могут применить один из трех подходов:
-
Перейти от переборного алгоритма к полиномиальному — например, использовать мемоизацию и снизить сложность алгоритма с до при решении задачи о редакционном расстоянии. Этот подход называется динамическим программированием, он помогает оценить алгоритмическую сложность нового решения
-
Ускорить алгоритм перебора, отбрасывая заведомо неподходящие варианты. Так работает метод ветвей и границ. В худшем случае, он работает медленно — со скоростью полного перебора. Здесь скорость зависит от того, с какими весами мы работаем и насколько точно оцениваем минимальное расстояние
-
Обнаружить способ решения сложной задачи, опираясь на правдоподобные рассуждения. Так работает жадный алгоритм, который на каждом шаге выбирает наилучшее локальное решение. Он не дает оптимального результата, но его все равно применяют, потому что на реальных данных жадное решение может быть оптимальным
Иногда жадный алгоритм дает наилучшее решение, и это можно доказать математически. Например, он оптимально решает задачу о размене монет, если речь идет о российской, американской, европейской или другой валюте.
Но так бывает не всегда. Чаще программисты ищут приближенные решения с помощью эвристик — приемов или методов, полезность которого не имеет теоретического обоснования, но подтверждается практикой. Иногда эвристика точно не дает лучшего решения, но ее применяют, если результат достаточно хорош.
Жадный подход — типичный пример эвристического алгоритма. Метод ветвей и границ также считают эвристическим, поскольку его производительность сильно зависит от функции оценки, а ее подбирают эвристически — исходя из природы данных. В то же время, алгоритмы динамического программирования эвристическими не считают, поскольку они находят оптимальное решение с предсказуемой полиномиальной сложностью.
В этом уроке мы познакомимся с эвристическим алгоритмом А* (читается как «А-звездочка»), который находит кратчайший путь в графе.
Кратчайший путь
Мы уже решали эту задачу, когда разбирали алгоритм поиска в ширину. Он работает для невзвешенных графов, поскольку строит путь из минимального количества ребер.
Но во взвешенном графе длина пути определяется не количеством ребер, а суммой весов. Поиск в ширину перестает справляться, поэтому во взвешенном графе кратчайший путь строят с помощью алгоритма Дейкстры.
Вершины, которые алгоритм Дейкстры проверяет на каждом шаге, похожи на расходящуюся волну. Как и при поиске в ширину, волна расходится не равномерно, а в сторону ближайших вершин:
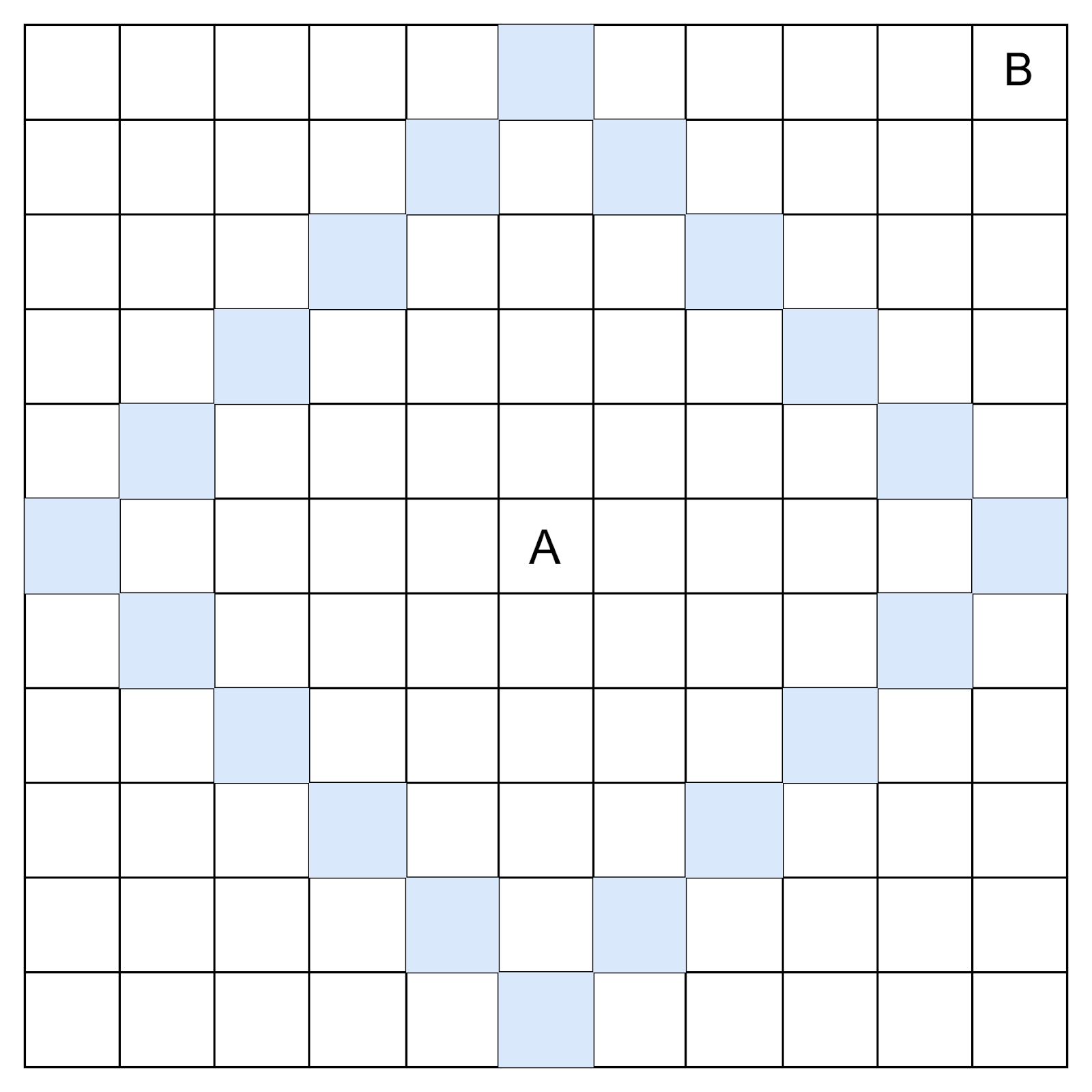
На этом рисунке мы видим волну, которая расходится из точки A при построении пути в точку B. Это классический поиск в ширину. Например, он применяется в играх, где на карте только дороги и препятствия.
Представим, что мы разрабатываем игру, в которой дороги бывают трех типов — трудная, обычная и легкая. Трудность дороги обозначим числами , или — это вес ребра, которое связывает соседние клетки.
Когда мы проходим клетку трудности , мы затрачиваем столько же усилий, сколько требуется на три клетки трудности . Поэтому речь идет о минимальной сумме значений в клетках, когда мы говорим о кратчайшем пути.
Во взвешенном графе волна будет выглядеть так:
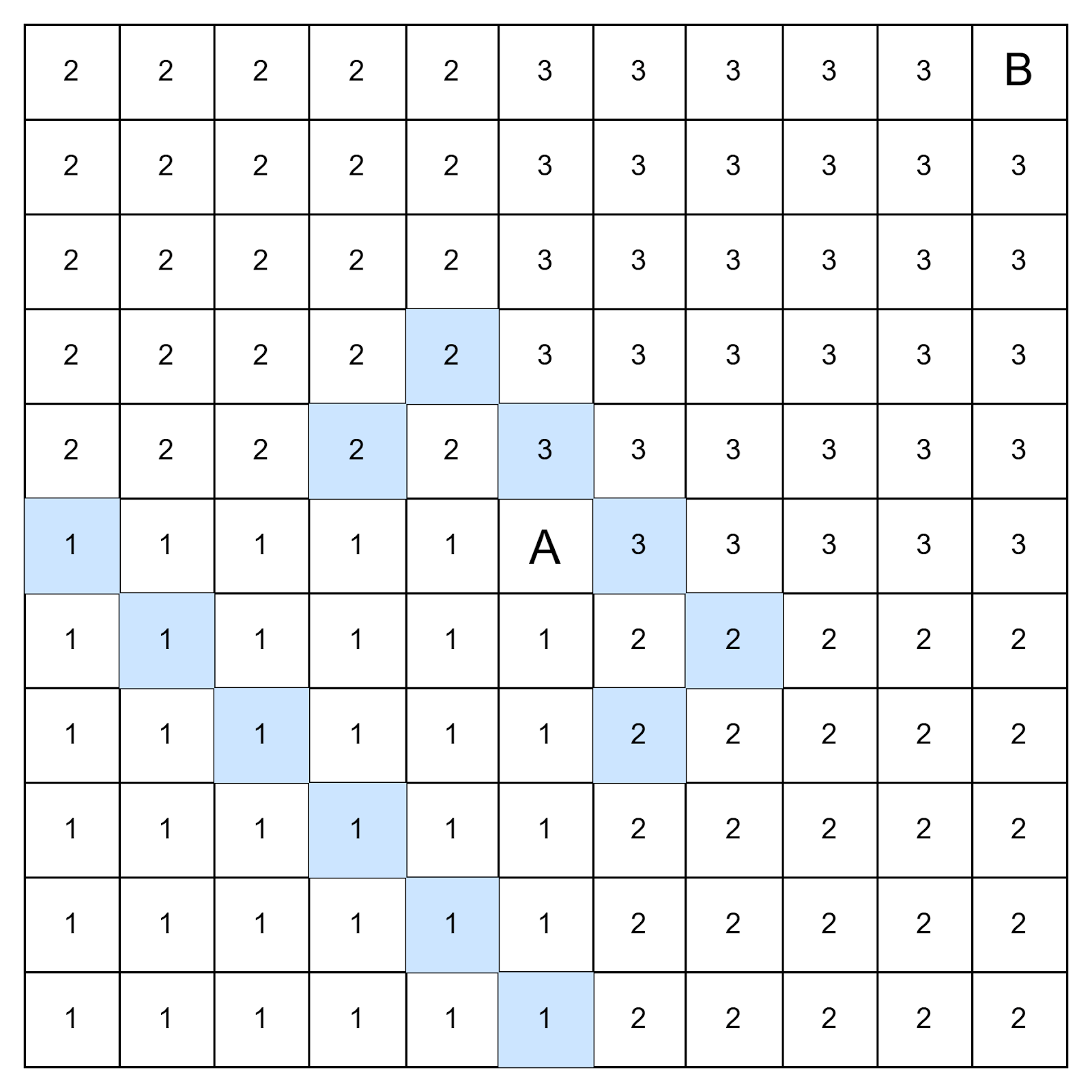
Дальше всего волна продвигается по легким дорогам, и это логично — иногда быстрее дать круг по легкой дороге, чем срезать по трудной.
У поиска в ширину и алгоритма Дейкстры один и тот же недостаток — они тратят ресурсы на плохие варианты путей.
В произвольном графе мы не можем судить, какой путь хороший, а какой — плохой. Но если речь идет о географической карте, то из вершины A очевидно надо строить путь в сторону вершины B:
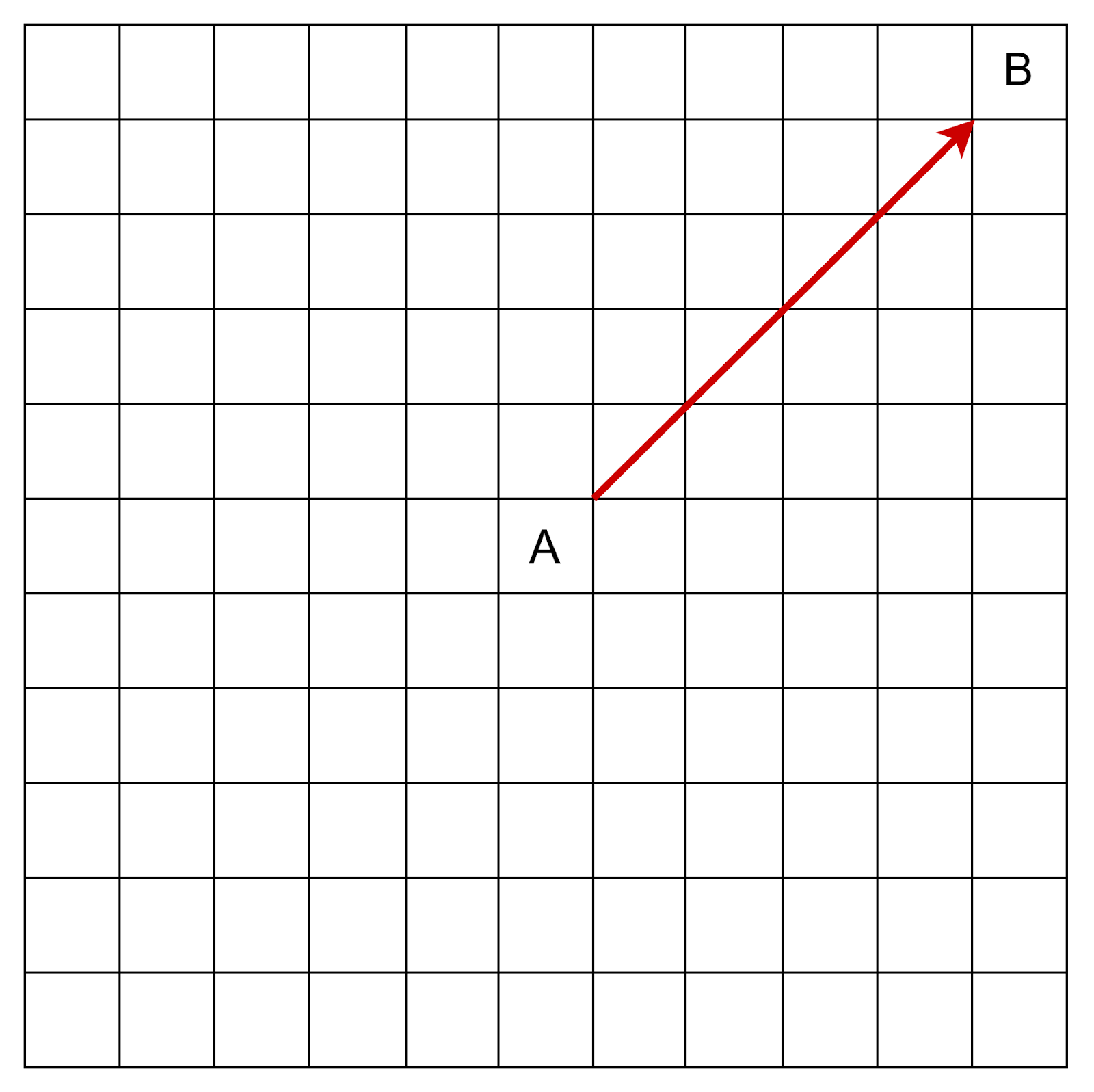
Так работает алгоритм А*. Он подходит для игровых и географических карт, поскольку опирается не геометрическое расстояние между точками. Также он подходит для любых графов, где можно подобрать хорошую эвристическую функцию нижней оценки расстояния.
Алгоритм А* умеет обходить препятствия. Он пробует напрямую пробиться к цели и находит кратчайший обходной путь, если прямой дороги нет.
Алгоритм А*
Вспомним, как работает поиск в ширину. Он находит всех соседей начальной вершины и помещает их в очередь. Затем в цикле алгоритм извлекает вершину из очереди, находит всех ее соседей и снова помещает в очередь. Поскольку очередь работает в соответствии с принципом «первый пришел — первый ушел», поиск в ширину перебирает сначала соседей, затем соседей соседей, затем соседей соседей соседей, и так далее.
Алгоритм А* действует похожим образом, однако вместо очереди использует очередь с приоритетом. Эту структуру данных мы не проходили, но столкнулись с ней, когда изучали метод ветвей и границ.
Элементы в такой очереди хранятся не сами по себе, а вместе с численной метрикой, которая называется приоритетом. Они извлекаются по возрастанию или убыванию приоритета — в зависимости от реализации.
Алгоритму А* нужны вершины, отсортированные по возрастанию приоритета. Приоритет рассчитывается как сумма двух значений:
-
Фактического расстояния от начальной до текущей вершины
-
Эвристической оценки расстояния от текущей вершины до конечной
Так это выглядит на схеме:
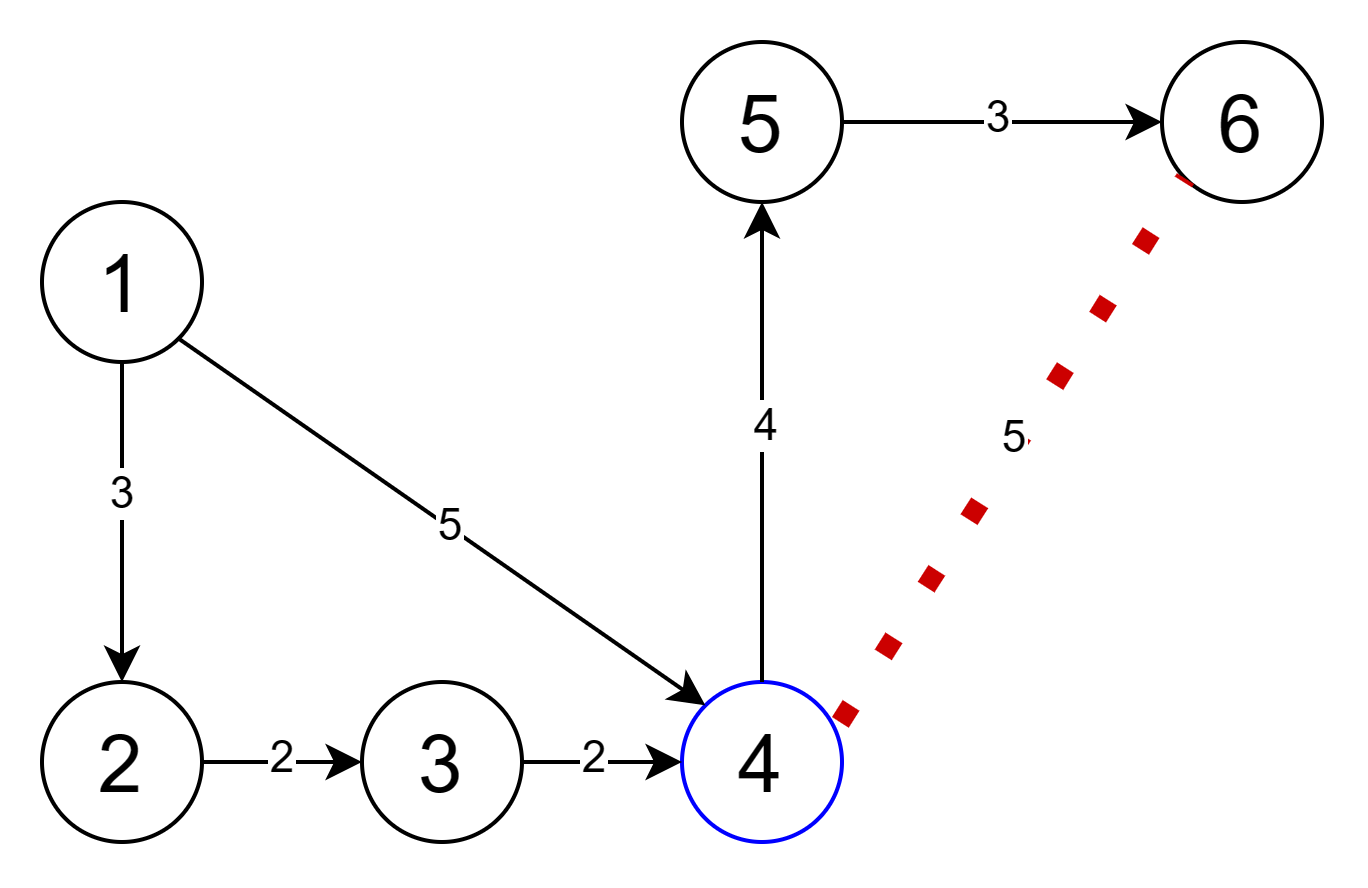
Здесь мы видим ситуацию при обработке вершины , когда мы ищем путь от вершины к вершине .
Минимальное расстояние между вершинами и и равно пяти. Существует обходной путь через вершины и — его длина равна семи, так что он длиннее.
Мы не знаем минимального расстояния между вершинами и . Это расстояние можно оценить геометрически как длину отрезка, который их соединяет (показан пунктирной красной линией). Из рисунка видно, что эта оценка также равна пяти.
Следовательно, приоритет вершины — это .
Алгоритм А* работает не только с картами, но и с произвольными графами. Для них можно придумать эвристику, чтобы оценить нижнюю границу расстояния.
А* — это развитие алгоритма Дейкстры, который тоже использует очередь с приоритетами, но учитывает только фактическое расстояние от начальной вершины. Именно поэтому алгоритм Дейкстры осторожно двигается во все стороны, в то время как А* из всех доступных вершин выбирает те, которые ближе к концу пути.
Реализация
Посмотрим на реализацию алгоритма в коде:
Нажмите, чтобы увидеть код
const astar = (map, fromRow, fromColumn, toRow, toColumn) => {
const pack = (row, column) => `${row}:${column}`;
const unpack = (cell) => cell.split(':').map((x) => parseInt(x, 10));
const visited = new Set();
const isValidNeighbour = (row, column) => {
if (row < 0 || row >= map.length) {
return false;
}
if (column < 0 || column >= map[row].length) {
return false;
}
const cell = pack(row, column);
if (visited.has(cell)) {
return false;
}
return true;
};
const minDistance = (fromRow, fromColumn, toRow, toColumn) => Math
.hypot(toRow - fromRow, toColumn - fromColumn);
const priorityQueue = [];
priorityQueue.shiftMin = function () {
let minIndex = 0;
let minPriority = this[minIndex].priority;
for (let i = 1; i < this.length; i += 1) {
if (minPriority > this[i].priority) {
minIndex = i;
minPriority = this[i].priority;
}
}
const result = this[minIndex];
this.splice(minIndex, 1);
return result;
};
priorityQueue.push({
priority: minDistance(fromRow, fromColumn, toRow, toColumn),
elapsed: 0,
cell: pack(fromRow, fromColumn),
path: [],
});
while (priorityQueue.length > 0) {
const top = priorityQueue.shiftMin();
const [row, column] = unpack(top.cell);
const path = [...top.path, top.cell];
if (row === toRow && column === toColumn) {
return path;
}
visited.add(top.cell);
const tryAddCell = (row, column) => {
if (isValidNeighbour(row, column)) {
const nextCell = pack(row, column);
const elapsed = top.elapsed + map[row][column];
const remaining = minDistance(fromRow, fromColumn, toRow, toColumn);
priorityQueue.push({
priority: elapsed + remaining,
elapsed,
cell: nextCell,
path,
});
}
};
tryAddCell(row - 1, column);
tryAddCell(row + 1, column);
tryAddCell(row, column - 1);
tryAddCell(row, column + 1);
}
return null;
};Реализация функции astar() — это расширенный поиск в ширину, которую мы разбирали в четвертом уроке. Мы используем очередь с приоритетами вместо обычной. В стандартной библиотеке JavaScript нет соответствующей структуры данных, но можно использовать подходящий класс сторонних разработчиков — например, SortedMap.
Мы сделали очередь приоритетов на базе массива, добавив в него метод shiftMin(). Этот метод извлекает из массива элемент с минимальным приоритетом:
const priorityQueue = [];
priorityQueue.shiftMin = function () {
let minIndex = 0;
let minPriority = this[minIndex].priority;
for (let i = 1; i < this.length; i += 1) {
if (minPriority > this[i].priority) {
minIndex = i;
minPriority = this[i].priority;
}
}
const result = this[minIndex];
this.splice(minIndex, 1);
return result;
};Обычно очередь с приоритетом реализуют поверх двоичного дерева, потому что это не самая производительная реализация. Зато одна из самых простых.
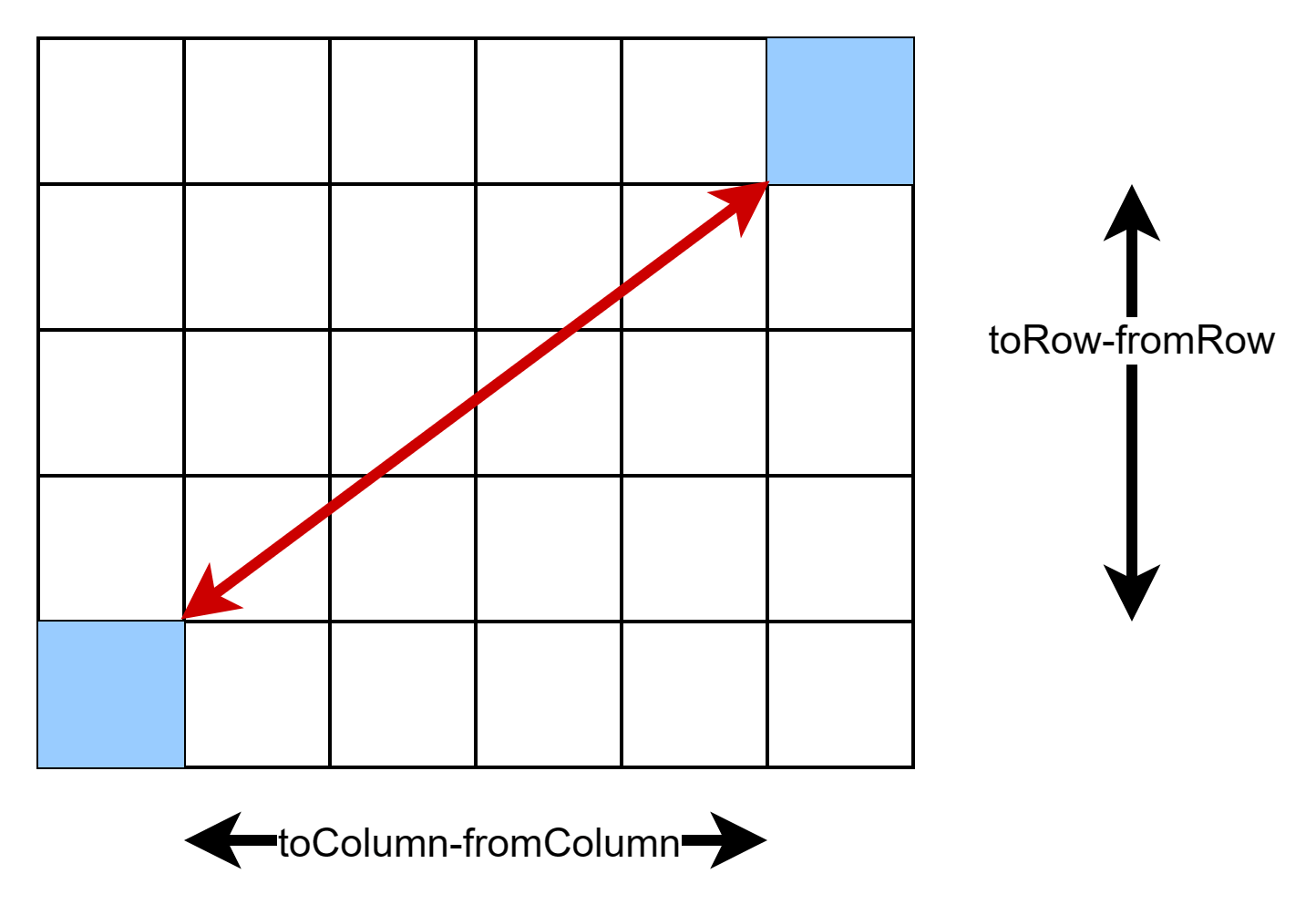
Чтобы оценить минимальное расстояние, считаем его как длину гипотенузы по теореме Пифагора:
const minDistance = (fromRow, fromColumn, toRow, toColumn) =>
Math.hypot(toRow - fromRow, toColumn - fromColumn);Функция isValidNeighbour() проверяет, можно ли продолжить путь в ячейку с указанными координатами. Идти дальше нельзя, если ячейка выходит за границы карты или если мы ее уже посещали — она есть в множестве visited:
const isValidNeighbour = (row, column) => {
if (row < 0 || row >= map.length) {
return false;
}
if (column < 0 || column >= map[row].length) {
return false;
}
const cell = pack(row, column);
if (visited.has(cell)) {
return false;
}
return true;
};Функция tryAddCell() добавляет ячейку в очередь с приоритетами, если isValidNeighbour() считает ее валидной:
const tryAddCell = (row, column) => {
if (isValidNeighbour(row, column)) {
const nextCell = pack(row, column);
const elapsed = top.elapsed + map[row][column];
const remaining = minDistance(fromRow, fromColumn, toRow, toColumn);
priorityQueue.push({
priority: elapsed + remaining,
elapsed: elapsed,
cell: nextCell,
path: path
});
}
};Каждый элемент очереди с приоритетами хранит четыре значения:
-
priority— приоритет, оценка длины пути (считается как сумма пройденного пути и оценки оставшегося пути) -
elapsed— пройденный путь (считается как сумма значений во всех посещенных ячейках) -
cell— ячейка, до которой добрался алгоритм -
path— путь до этой ячейки
Исходные данные для функции astar() — двумерная карта или массив, где каждый элемент содержит трудность прохождения этой клетки. Минимальное значение 1 соответствует обычной клетке. Значение 3 означает клетку, которая соответствует трем обычным клеткам. Очень большие значения (в нашем случае 999) означает непреодолимое препятствие:
const map = [
[ 1, 1, 2, 2, 2, 2, 2, 2, 2, 1 ],
[ 1, 1, 2, 2, 2, 2, 2, 2, 2, 1 ],
[ 1, 1, 1, 999, 999, 999, 999, 2, 2, 1 ],
[ 1, 1, 1, 1, 1, 3, 999, 2, 1, 1 ],
[ 1, 1, 1, 1, 1, 3, 999, 1, 1, 3 ],
[ 1, 1, 1, 1, 2, 3, 999, 1, 2, 3 ],
[ 1, 1, 1, 1, 2, 3, 999, 1, 3, 4 ],
[ 1, 1, 1, 1, 1, 3, 3, 1, 3, 4 ],
[ 1, 1, 1, 1, 1, 3, 3, 1, 3, 4 ],
[ 1, 1, 1, 1, 1, 1, 1, 1, 1, 4 ],
];На схеме ниже показано, как выглядит эта карта. Области с более насыщенным цветом труднее для прохождения. Черным цветом мы обозначили непроходимые участки карты — стены или заборы:
astar(map, 5, 4, 0, 9) // [
// '5:4', '6:4', '7:4',
// '7:5', '7:6', '7:7',
// '6:7', '5:7', '4:7',
// '4:8', '3:8', '3:9',
// '2:9', '1:9', '0:9'
// ]https://replit.com/@hexlet/algorithms-graphs-astar
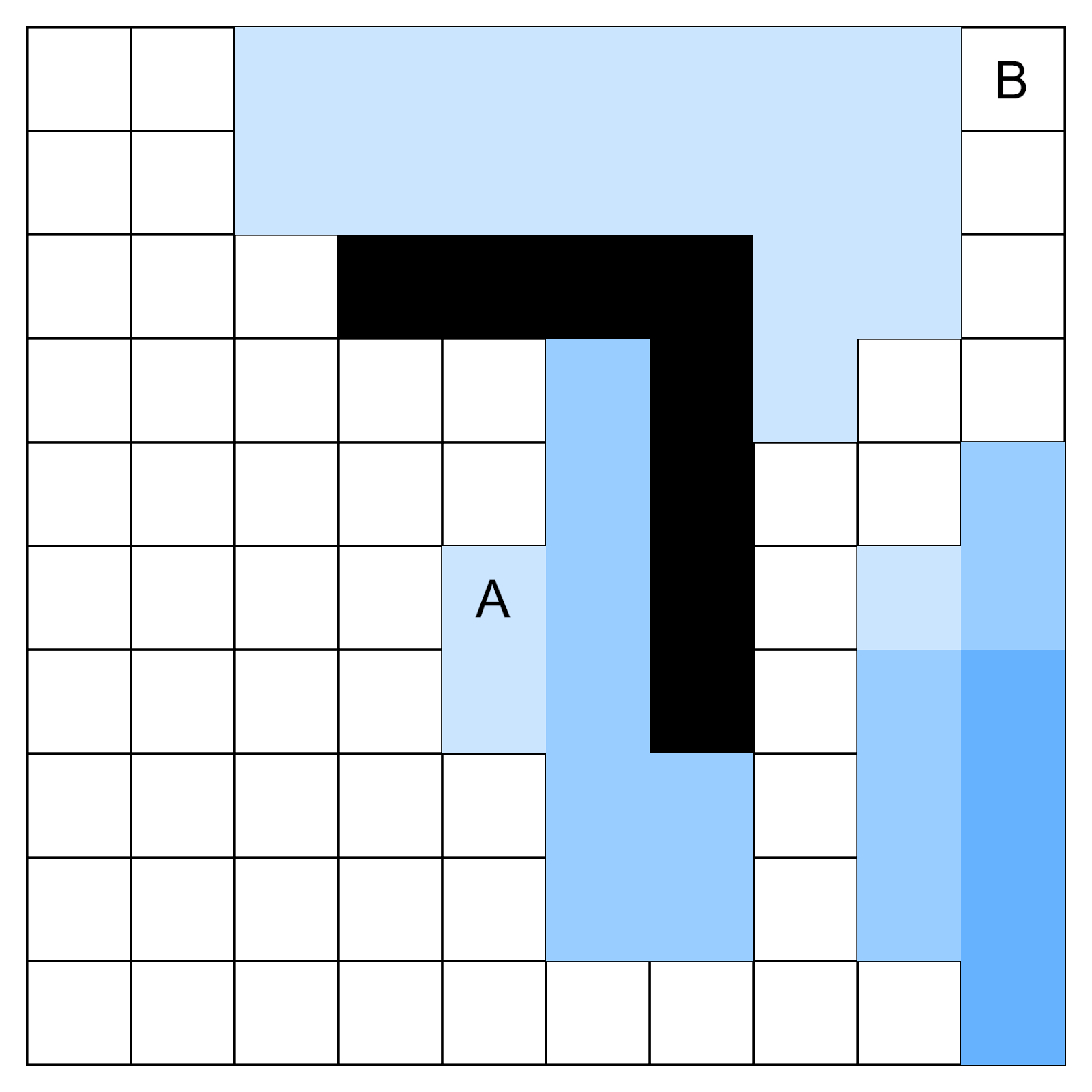
На схеме мы видим маршрут, построенный алгоритмом. Большей частью он проходит по простым клеткам. Такой же маршрут построил бы и алгоритм Дейкстры, затратив больше времени.
Алгоритм А* работает быстрее благодаря эвристике. Мы знаем, что граф на самом деле представляет собой карту, и мы можем геометрически оценить расстояние между клетками:
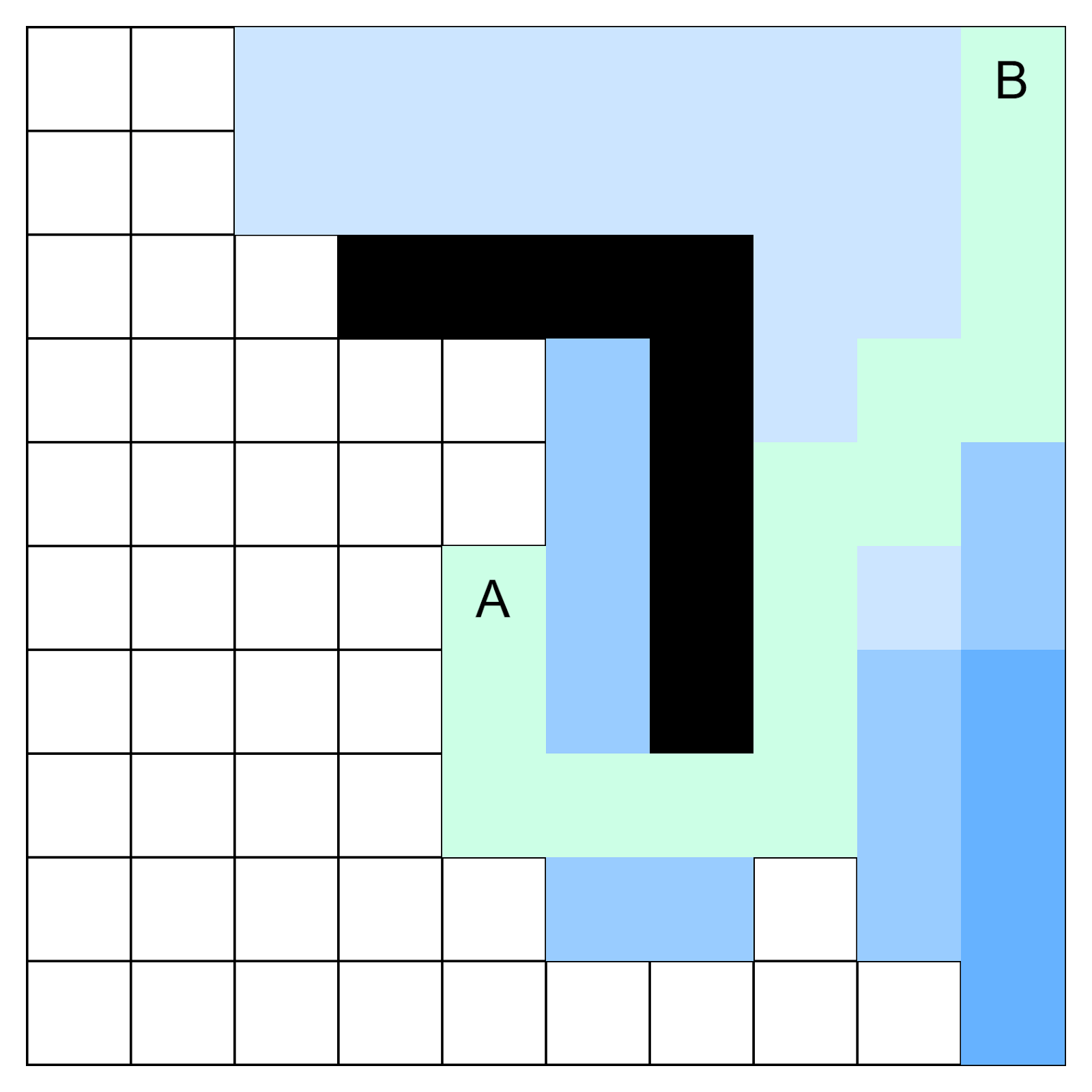
Выводы
Повторим ключевые выводы этого урока:
-
Эвристические алгоритмы широко применяются для решения задач класса NP
-
Эвристическим называется алгоритм, который позволяет найти не оптимальное, но достаточно хорошее решение — например, жадный алгоритм
-
Также эвристическим называется алгоритм, который может сократить полный перебор — например, метод ветвей и границ
-
Ко второму варианту относится и алгоритм А*, который позволяет быстро построить кратчайший путь на географической карте
-
Алгоритм А* — это расширенная версия алгоритма Дейкстры, которая пытается минимизировать длину пути от начальной до конечной клетки
-
Полная длина для каждой клетки рассчитывается как сумма двух слагаемых
-
Пройденного пути — это точное значение
-
Оставшегося пути — это предполагаемая оценка
-
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
