Алгоритмы на графах
Теория: Практическое применение графов
Вы уже знаете, что граф — это фигура, состоящая из вершин и соединяющих их ребер. С помощью графов решают многие важные классы задач, с которыми мы познакомимся далее в этом уроке.
Выбираем оптимальный путь на метро
Представьте себе схему метро крупного города: скорее всего, в центре будут пересекаться несколько разных веток. Из-за этого получается, что проехать между станциями можно разными способами.
Например, в московском метро от станции «Фрунзенская» до станции «Полянка» можно доехать двумя способами:
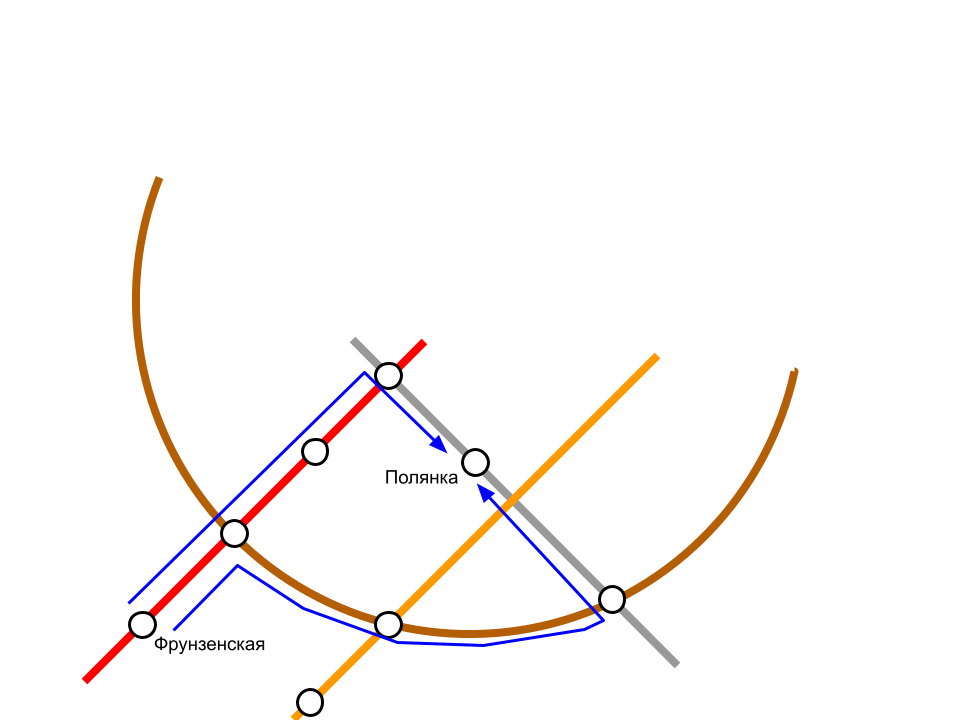
Попробуем определить, какой из этих маршрутов короче. Чтобы посчитать общее время в пути, нужно знать, сколько времени занимает проезд между соседними станциями и сколько времени занимает переход.
По сути, карта метро — это граф. Немного дорисуем его, чтобы обозначить переходы с ветки на ветку. На новом рисунке проставим время в минутах рядом с каждым ребром — перегоном между соседними станциями или переходом:
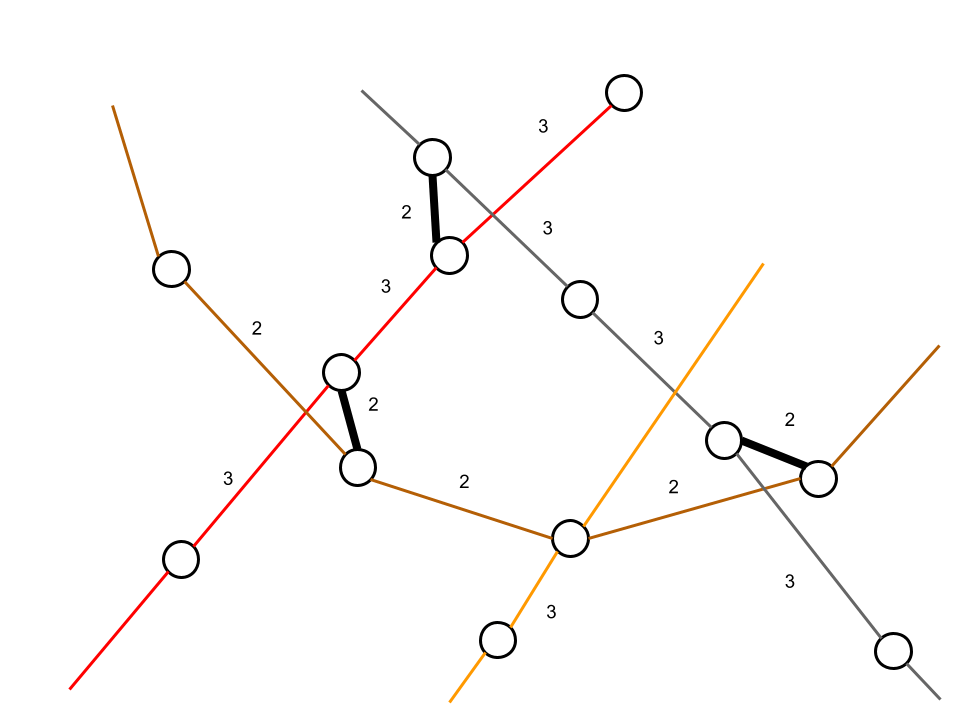
Теперь можно вычислить полное время на каждом маршруте и выбрать самый короткий. Решение выглядит обманчиво простым. Люди интуитивно отбрасывают заведомо плохие варианты и сразу видят два подходящих маршрута. У компьютера интуиции нет — он переберет все маршруты, которых в действительности гораздо больше двух.
Задачи такого рода в программировании относят к классу «задачи о кратчайшем пути». Число, приписанное каждому ребру, называют весом ребра, а сам граф называют взвешенным.
Неочевидно, почему используют слово «вес», а не «длительность пути». Этому есть объяснение. За названием «взвешенные графы» скрываются разные задачи, решаемые одним и тем же способом. Для некоторых задач числа обозначают время, для других — расстояния, для третьих — денежные суммы, для четвертых — вес.
Этот термин широко используется в математике — там есть весовые коэффициенты или весовая функция. Так что программисты получили этот термин в наследство от математиков.
Строим маршрут по автомобильным дорогам
Рассмотрим еще одну задачу — построение автомобильного маршрута. Для начала нужно определиться с ребрами и вершинами:
- Ребрами будут считаться сами дороги
- Вершинами — развилки и пересечения дорог
Здесь мы сталкиваемся с одной сложностью, которой не было в задаче с метро. В отличие от метро, автомобильные дороги могут быть с односторонним движением. Рисуя граф, мы должны учитывать эту особенность.
Граф движения по городу может выглядеть так, как показано на картинке ниже. Голубым цветом нарисованы проспекты, а зеленом — односторонняя часть пути во дворах:
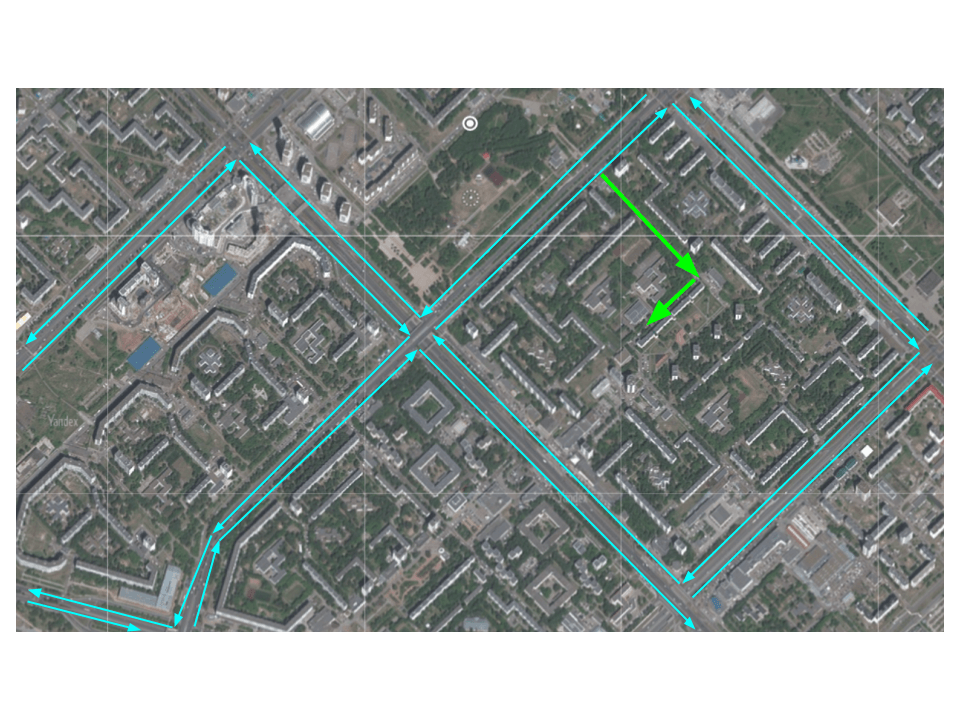
На этот граф мы добавили стрелки, которые показывают направление движения:
- Если дорога односторонняя, мы рисуем ребро со стрелкой
- Если дорога двухсторонняя, мы рисуем два ребра с противоположными стрелками
Если у ребер графа задано направление, такой граф называют направленным или ориентированным. Часто название «ориентированный граф» сокращают до «орграфа».
Обратите внимание, что граф автомобильных дорог не только ориентированный, но и взвешенный — ведь нам нужно находить по нему оптимальные маршруты. В отличие от метро, на автомобильных дорогах бывают пробки. Поэтому мы не можем заранее присвоить ребрам точный вес — придется обозначать его как время проезда без учета пробок.
Выбираемся из лабиринта
Иногда нам не нужно выискивать идеальный маршрут — достаточно выяснить, можно ли его построить. Для примера представьте, что нам надо выбраться из лабиринта:

В таком случае мы согласимся на любой путь и не будем уточнять, если ли пути покороче.
Есть несколько стратегий выхода из лабиринта. Например, есть правило правой руки, которое предлагает такую стратегию:
- Мы кладем правую руку на стену и начинаем идти по лабиринту
- Если мы пришли к развилке, всегда выбираем правый путь
- Если мы пришли в тупик, возвращаемся к последней развилке и идем в следующий по счету коридор
- Если все коридоры закончились тупиком, возвращаемся к предпоследней развилке и продолжаем обход справа налево
Конечно, коридоры можно обходить и слева направо, тогда речь будет идти о правиле левой руки — оно работает абсолютно так же. Здесь важно придерживаться всегда одной стороны, не смешивая повороты направо и налево.
Как и в случае с автомобильной картой, вершинами графа будут только места развилок и тупики. Посмотрим, как будет выглядеть маршрут по лабиринту:
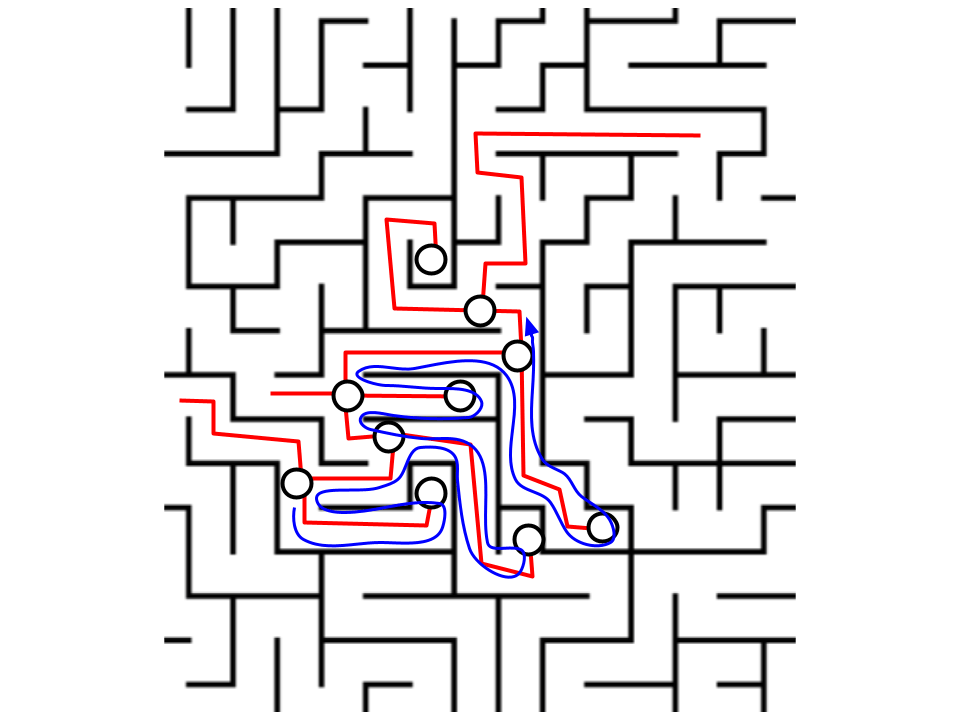
Рассмотрим этот рисунок подробнее:
- Красными линиями обозначены ребра графа
- Кружками обозначены вершины
- Направление обхода графа показано синим цветом
Стратегия предполагает, что мы пытаемся пройти как можно глубже, а если попадаем в тупик, возвращаемся назад. На рисунке это тоже видно — синяя линия часто идет в двух направлениях.
Такой способ движения по графу называется обходом в глубину*. Этот алгоритм применяется для поиска вершины с определенными свойствами, поэтому часто употребляют похожий термин — «поиск в глубину». В профессиональной литературе вы можете встретить аббревиатуру DFS — depth first search, то есть «поиск сначала в глубину».
Этот алгоритм прекрасно работает, если в лабиринте нет замкнутых коридоров или петель. Если мы попадем на петлю, мы можем вечно ходить по одному и тому же коридору, как показано на рисунке:
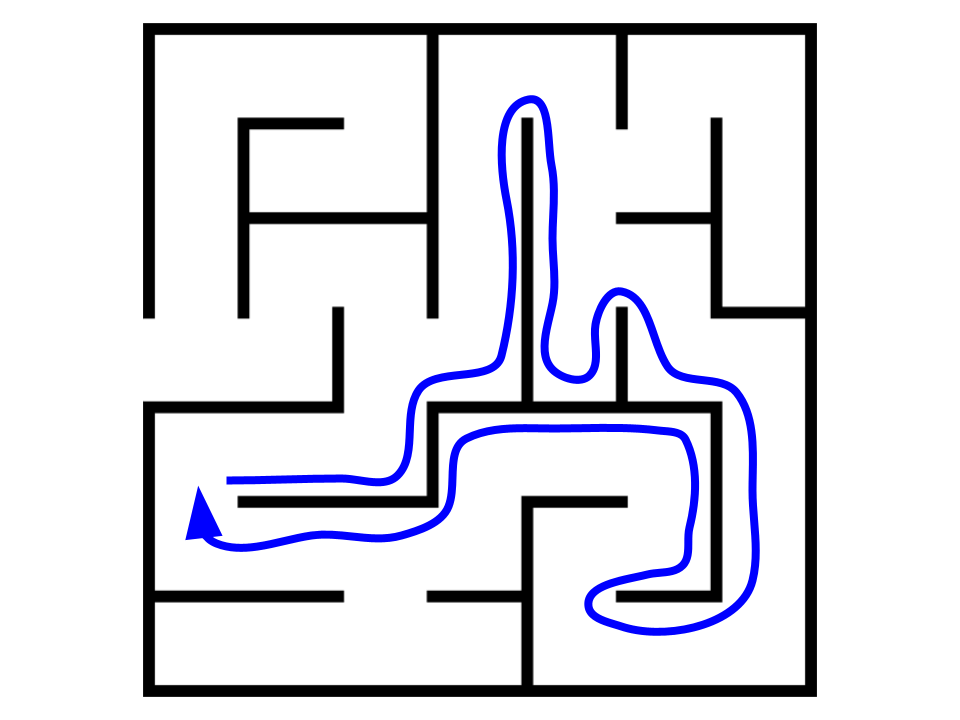
Если мы нарисуем граф для такого лабиринта, мы обнаружим такую же петлю. Графы с петлями называются циклическими и требуют осторожности при обходе:
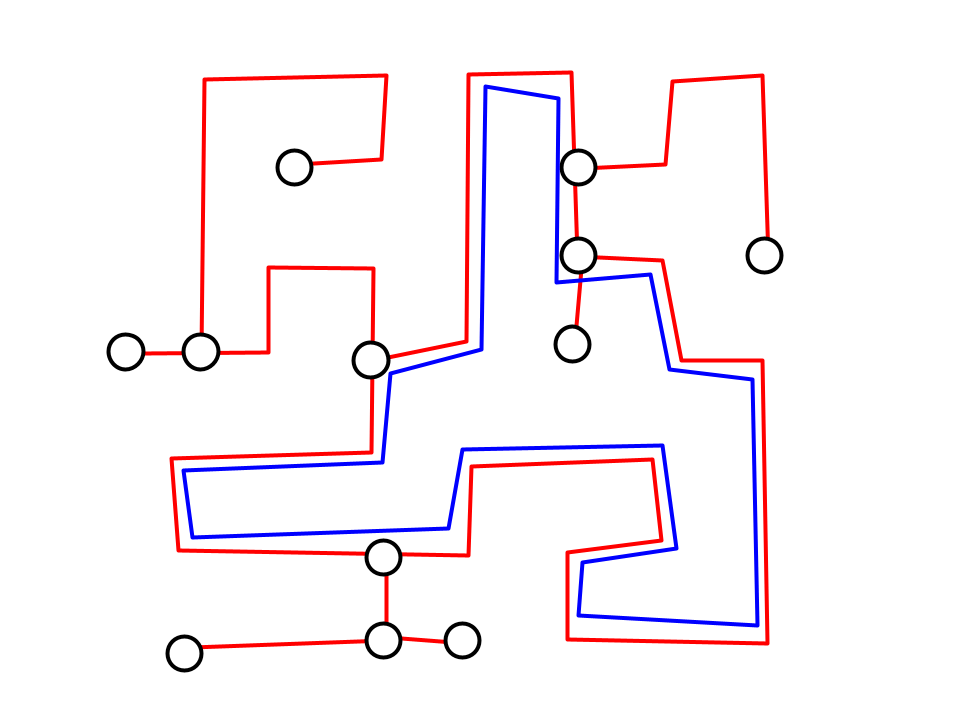
Обходя лабиринт с петлями, можно помечать посещенные развилки мелом. Встретив пометку, мы узнаем, что попали в цикл. Действовать в этом случае надо так же, как и в тупике — развернуться и идти назад.
Обходим препятствия
В ролевых и стратегических играх пользователь управляет игровыми юнитами. Например, он может отправить боевой или строительный юнит на другой конец карты. Как правило, на карте встречаются препятствия — непроходимые горы и озера.
Игровая карта может выглядеть так:

Двигаясь по карте, юниты уверенно огибают преграды и достигают цели за кратчайшее время. Разберемся, как это работает.
Как и в предыдущих задачах, мы сначала решаем, что будет считаться ребрами и вершинами графа. В компьютерных играх вершины размещают в клетках карты. Ребра связывают соседние пустые клетки, в которых нет гор или озер.
Представим, что нам надо добраться из вершины Н в вершину К:
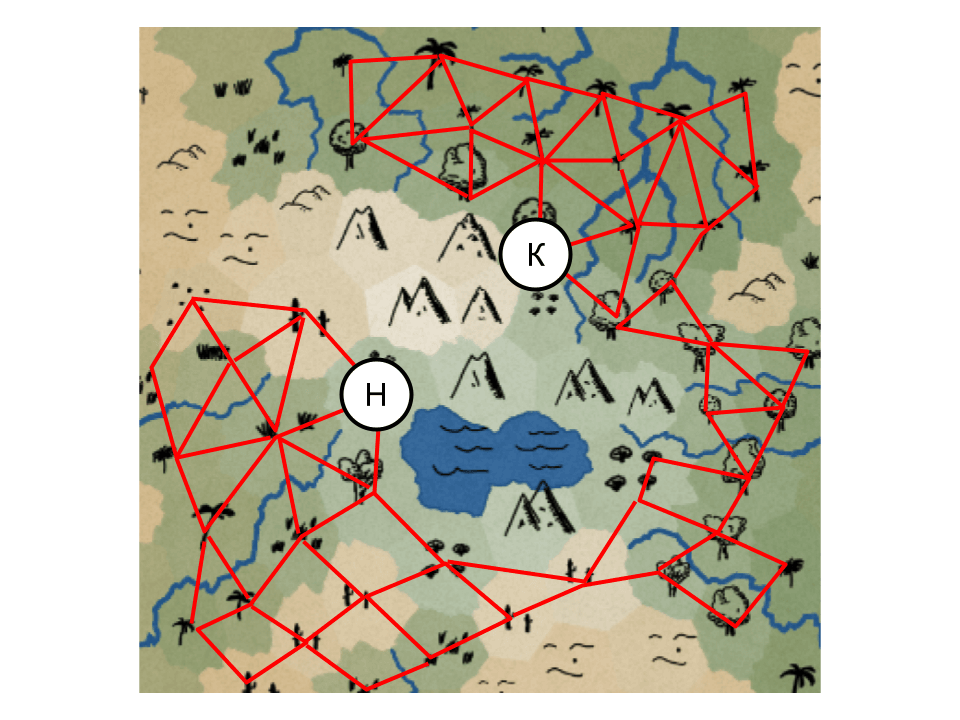
Поиск в глубину поможет найти дорогу, но если на карте много поворотов и узких проходов, эффективнее будет другой алгоритм. Он называется волновым, потому что напоминает волны, кругами расходящиеся на воде от брошенного камня:

Сначала мы проверяем соседей начальной вершины, затем — соседей соседей, и так далее, каждый раз удаляясь от начальной вершины на один шаг. В какой-то момент очередной круг доберется до конечной вершины. Это будет означать, что путь найден:
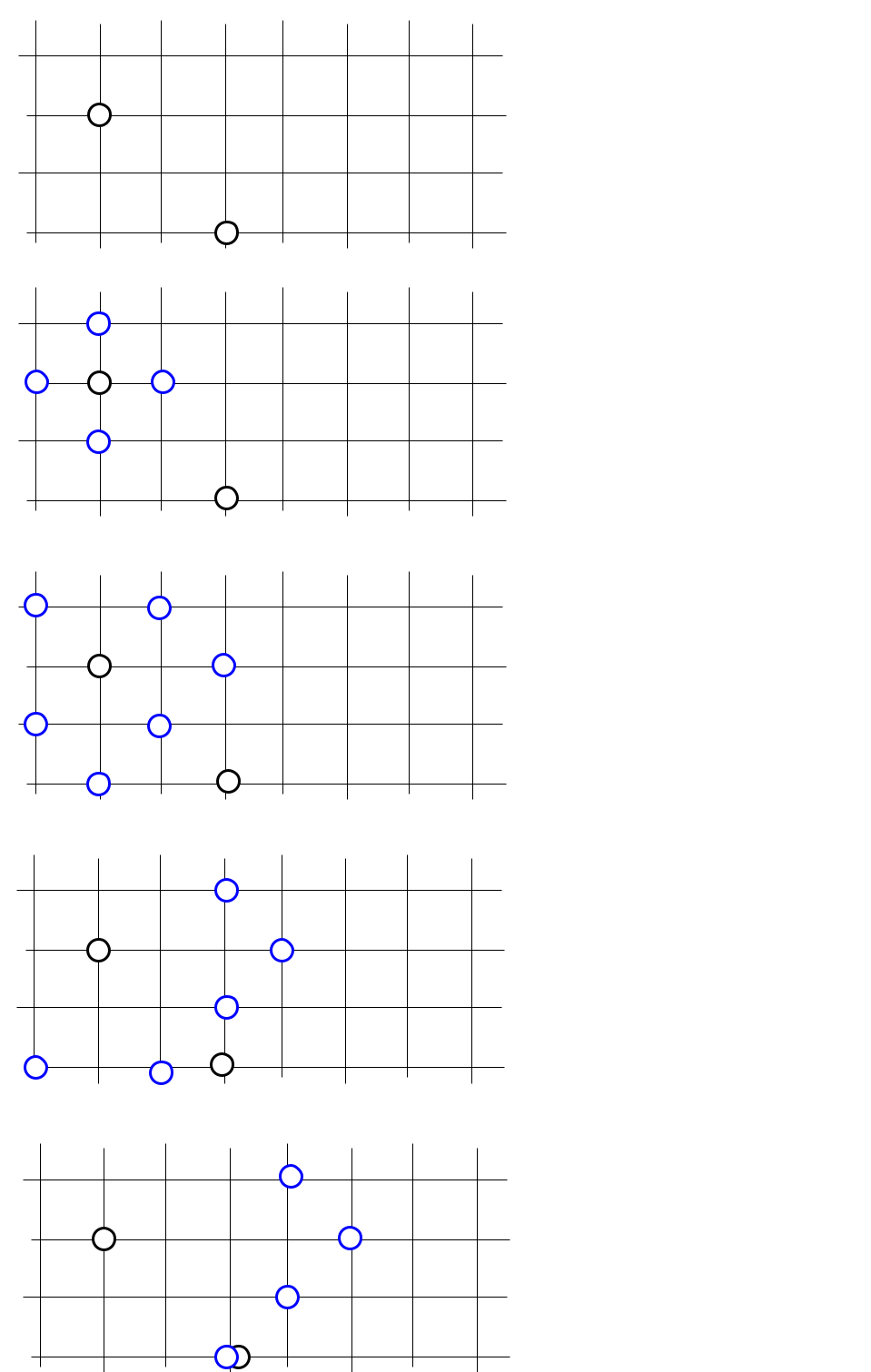
Другое название этого алгоритма — поиск в ширину или BFS, breadth first search. Он позволяет найти маршрут с наименьшим количеством ребер. Впрочем, у него гораздо больше применений. В частности, одна из его модификаций позволяет закрашивать на изображениях замкнутые области произвольной формы.
Может показаться, что задачи на графах касаются в первую очередь карт или каких-то картинок, но это не так. Далее мы узнаем, как графы применяют при решении экономических и логистических задач.
Считаем сдачу
Одна из задач, которую решает программное обеспечение банкоматов и вендинговых аппаратов — выдача сдачи. Как правило, автоматы пытаются выдать сдачу наименьшим количеством банкнот или монет.
Номиналы монет подбираются так, чтобы ими можно было выдать любую сумму. Например, сдачу в 8 рублей можно выдать тремя монетами: 5 рублей, 2 рубля и 1 рубль.
Чтобы посчитать сдачу, можно использовать простой алгоритм выбора монет:
- Пока можем, набираем сумму самыми крупными монетами
- Затем переходим к следующим по номиналу монетам, и так далее
Проблема в том, что иногда в автомате заканчиваются монеты определенного номинала. Отсутствие двухрублевых монет не скажется на работе алгоритма: он выберет одну пятирублевую монету и три однорублевых.
Но если в автомате закончатся рублевые монеты, алгоритм не сможет вернуть сдачу в 8 рублей. Сначала он выберет монету в 5 рублей, потом монету в 2 рубля, а дальше начинаются сложности — надо выбрать монету в 1 рубль, а они закончились.
Даже в этом случае задача может быть решена — сдачу можно выдать четырьмя монетами по 2 рубля. Проблема в том, что простой алгоритм этот вариант не найдет.
Более сложный алгоритм работает на графах. Это может показаться странным, потому что не совсем очевидно, как они сюда относятся:
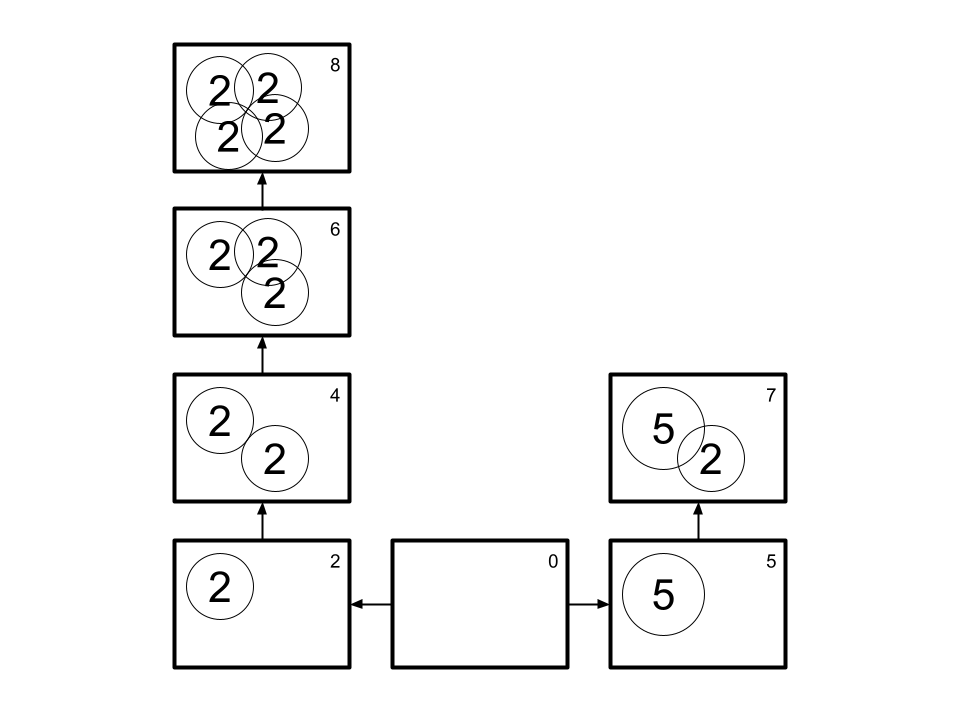
На рисунке мы видим, что каждый узел графа может содержать набор монет. Двигаясь по стрелкам, мы добавляем к набору одну новую монету. Мы начинаем с пустого узла, в котором нет ни одной монеты. Далее мы ищем узлы, где достигается нужная сумма в 8 рублей.
У нас нет карты, которая стала бы основой для графа, потому что мы не храним все узлы графа. Вместо этого, можно генерировать новые соседние узлы по мере надобности, следуя простым правилам.
Подобные графы часто встречаются в программировании, они называются неявными. Неявный граф не требует хранения своих узлов — узлы можно вывести или вычислить.
Хорошим кандидатом для решения задачи о монетах будет алгоритм поиска в ширину. Мы продвигаемся во всех направлениях от пустого узла, в поисках узлов, содержащих сумму 8 рублей.
К сожалению, этот алгоритм не очень эффективен. Нам надо дать сдачу наименьшим числом монет, поэтому мы можем всегда начинать с монеты самого крупного номинала. Это решение похоже на то, которые мы рассматривали в начале. Разница только в том, что у нас остается возможность найти правильный ответ, даже если каких-то номиналов не хватает.
Такой поиск похож на поиск в ширину, у которого есть предпочтительное направление. Мы можем использовать его, потому что у нас есть дополнительная информация о задаче.
При работе с графами программисты часто используют подобную информацию для того, чтобы ускорить алгоритм. Такие модификации называются информированными алгоритмами*. Классические алгоритмы без дополнительной информации называют неинформированными.
Выводы
Повторим ключевую мысль из этого урока — графы решают множество практических задач, с которыми мы сталкиваемся каждый день. Изучив эту тему, вы сможете:
- Находить кратчайшие маршруты на карте метро — решать задачи о кратчайшем пути с помощью взвешенных графов
- Строить пути на автомобильных картах с помощью ориентированных графов
- Искать выход из лабиринта по правилу правой руки, применять обход в глубину и работать с циклическими графами
- Задавать маршруты для юнитов в компьютерных играх с помощью волновых графов
- Правильно давать сдачу в вендинговых автоматах с помощью поиска в ширину
